Математическое моделирование двумерных течений газа с использованием RKDG-метода на структурированных прямоугольных сетках

Разрывный метод Галеркина (RKDG-метод) относится к числу наиболее эффективных численных методов, позволяющих исследовать математические модели, допускающие разрывные решения, а также развитие неустойчивостей.

Суть метода сводится к повышению точности моделирования не за счет расширения шаблона аппроксимации, а за счет увеличения порядка аппроксимации численного решения на каждой ячейке. Благодаря этому RKDG-метод получил широкое распространение в вычислительной аэроакустике [1, 2] и гидродинамике [3].

Согласно теореме Годунова алгоритм поиска численного решения RKDG-методом, обеспечивающий повышенный порядок точности, требует дополнительной монотонизации решения для подавления нефизичных осцилляций. Для этих целей обычно используют функции-ограничители, иначе называемые лимитерами [4]. Вследствие применения лимитеров порядок точности численного метода в общем случае может снижаться до первого, поэтому их следует применять лишь на тех ячейках, где нарушается монотонность решения. Для поиска таких «проблемных» ячеек используют функции-индикаторы.

Одним из способов обеспечения монотонности решения является использование MUSCL-схем (Monotonic Upstream-Centered Scheme for Conservation Laws) [5, 6]. Широкое использование подобных лимитеров связано прежде всего с простотой их реализации, однако качество разрешения разрывов при этом остается невысоким.

Методические исследования, проведенные для одномерных задач [7], показывают высокую эффективность другого подхода, связанного с использованием технологии реконструкции решения на основе подхода WENO (Weighted Essentially Non-Oscillatory). Исходные идеи, положенные в основу схем типа WENO, ограничивают применимость данных методов в многомерном случае, поскольку они требуют расширенного шаблона аппроксимации для реконструкции решения с высокой точностью [8]. Однако разработаны модификации этого алгоритма (например, WENOS [9] и HWENOSC [10]), которые позволяют сохранить компактность шаблона аппроксимации.

Целью работы является сравнительный анализ применения наиболее простого лимитера типа WENO (WENO S) и MUSCL-лимитера при решении двумерных задач газовой динамики на структурированных прямоугольных сетках. Для этого разработан программный комплекс, реализующий RKDG метод с линейными базисными функциями применительно к решению системы уравнений газовой динамики в двумерной постановке.

2.    Система уравнений газовой динамики

Нестационарная система уравнений газовой динамики, описывающая двумерные течения идеального сжимаемого нетеплопроводного газа, имеет вид [11]:

аи ағ(и) dG(U) St дх ду где

U = \p,pu,pv,pw,eT,

F = [pu,piP + p,puv,puw,(e + p^uf,              (2)

G = Vpv,pvu,pv² + p,pvw,(e+ рУ\^т.

Здесь U - вектор консервативных переменных; F, G - векторы потоков консервативных переменных; р - плотность; v = [m,v,w]^t - вектор скорости; е = рс + ^рдг + v² + w²) - полная энергия единицы объема; р - давление газа; s - удельная внутренняя энергия.

Связь р, р и Е определяется уравнением состояния газа:

p = pE,                            (3)

где у > 1 - показатель адиабаты.

Систему Ошибка! Источник ссылки не найден. -Ошибка! Источник ссылки не найден, можно записать в квазилинейной неконсервативной форме:

Эта система уравнений является гиперболической, все собственные значения матриц А и В действительны и существует полная система собственных векторов. Следовательно, матрицы могут быть диагонализированы и записаны в виде

A = Q^Qf, П^МЛ

B = tfRxBrfL,   siBR=\^ly, где Н =dia^^,...,P^}, j = А,В - диагональные матрицы, составленные из собственных значений матриц А и В ; QR,QR - матрицы правых и левых собственных векторов соответственно.

Будем рассматривать систему уравнений (1) в области [0;Лх]х[0;Л^]х(0;Т] и зададим начальное условие вида

U(x,y,O) = Uo(x,y).

3.    Численный метод 3.1    Общая схема RKDG

Введем на рассматриваемой пространственной области равномерную по каждому направлению прямоугольную сетку с шагами h_x = L_X!N_X и hy=L_yINy соответственно, состоящую из N_x-N_y ячеек 1ц с центрами (Л^у) = №-^^>_хXj - ^1/2)^у) и границами

(^±1/2, Уу ±1/2) = (^ ± А/2, уj ± h!^ i = \,N_x, j = \ ,Ny.

Для использования RKDG-метода определим пространство кусочнонепрерывных функций У^ = ^р ; р\ еР^ЦцА , которые являются многочленами степени не выше к на каждой ячейке 1ц . Для поиска численного решения системы (1), (4) умножим уравнения системы на тестовые функции v(x,y) е V^ и проинтегрируем полученные соотношения по каждой ячейке.

Приближенное решение задачи будем искать в виде

^іР^УА = T/L^4ty^4x,y\ iJs=0

где кФ^ ^УА^=О - ортонормированные базисные функции, определенные на ячейке 1ц следующим образом:

ФцЧ^х,А = J— , фР\х,у^ = 1^-(х-х,), фР\х,у) = І^г-(у-уц)-^Һ_хҺу               Һ_ХҺу                     Һ_ХҺу

Индекс «Л» у численного решения задачи для краткости будем опускать. Используя в качестве пробных функций базисные, получим систему обыкновенных дифференциальных уравнений относительно коэффициентов U^, г = 0,1,2:

--I ¥ц-----dxdy- I G,,------dxdy + dt , дх j ду У                У

• + J ^уф*ір^йх- J ^уФ^ірАх* J СцфРгіу- J Gj^pdy = O, (5)

• 3.2    Численные потоки

BIij,R              BIij,L               BIij,T               5Iij,B

Здесь Ғ^ =Ғ(и,у(л:,у,ОХС_гу =G^ 91_{у £} , 91_уД, dI_ijT и 9I_{ij B} обозначают левую, правую, верхнюю и нижнюю границы ячейки 1у соответственно.

При решении системы ОДУ (5) требуется обеспечивать порядок точности, соответствующий порядку аппроксимации по пространственным координатам. Для этого целесообразно использовать методы Рунге - Кутты, причем среди методов высокого порядка необходимо выбирать те, которые обеспечивают наименьший уровень временной немонотонности численного решения. В данной работе используется TVD-метод Рунге - Кутты второго порядка:

U* =U"+zL_a(U"), _l»h ₌^_l;,,₊^ ₊ ^^

где г - шаг по времени; L/,(U) - правая часть уравнения (5); U” и U"⁺¹ - приближенные решения на текущем и следующем временных слоях соответственно.

Численное решение уравнения (Г) терпит разрывы на границах ячеек, поэтому аналитические потоки F и G в уравнении (5) следует заменить численными потоками F и G . Их можно вычислить по предельным значениям численного решения на ячейках, соседних к рассматриваемой границе, используя приближенные решения задачи Римана о распаде произвольного разрыва, по аналогии со схемами годуновского типа. В данной работе используются численные потоки Лакса - Фридрихса (LF), HLL и HLLC [11].

• 3.3    Лимитеры

С одной стороны, использование для аппроксимации решения на ячейках базисных функций высокого порядка должно приводить к повышению точности метода. Однако с другой стороны, получаемая численная схема становится немонотонной, что может выражаться в возникновении нефизичных осцилляций приближенного решения, особенно в окрестности разрывов. Для подавления таких осцилляций применяются специальные нелинейные ограничители - лимитеры [4, 8], обеспечивающие уменьшение наклона численного решения в проблемной с точки зрения немонотонности ячейке.

В данной работе использованы лимитеры WENOS (simple) [9] и MUSCL [13]. Лимитеры применены к численному решению покомпонентно; лимитер WENOS может применяться двумя способами:

• •    путем реконструкции решения на шаблоне, состоящем из самой ячейки и четырех соседних ячеек;

• •    в виде полусуммы независимых реконструкций вдоль каждой из осей. Большинство известных ограничителей, таких как, например, MUSCL (основанный на minmod-свойстве), ухудшают точность, так как ошибочно применяются в областях, где решение является гладким. Это нивелирует эффект от введения полиномиальной аппроксимации решения на соседних ячейках. Таким образом, лимитеры следует применять лишь на тех ячейках, где монотонность решения нарушается. Поэтому первый шаг алгоритма монотонизации должен быть связан с обнаружением так называемых «проблемных ячеек», т.е. поиском ячеек, производные решения на которых необходимо ограничить. В данной работе для данных целей используется индикатор проблемных ячеек KXRCF [14].

4.    Результаты тестовых расчетов 4.1    Распространение акустического импульса

Рассмотрим распространение цилиндрической акустической волны, вызванное малым возмущением плотности. Начальное возмущение задано в центре прямоугольной области [0,Zx]x[0,Zv] функцией

Р\х^ |_/=0= f exp[-2(^-0.5Z_%)² -2(у-0.5С^)²) е = IO"⁶

Следует отметить, что такое возмущение является точным решением системы линеаризованных уравнений Эйлера (1), записанной для малых возмущений плотности р', компонент скорости и', v' и давления р' (акустическое приближение):

U ='vp',p_ou',p_oV,p_ow^,,p^,T,

Ғ =Үр'и₀ + р₀и\р_оіі _оиЧ р\р_ои _ov\p_oii _ow\u^^^

G =Vp'v0 + P0v,.P0v0ll'.P0v0v' + P'.PoVow'^OP' + 1POV'AT, где Po , iiq , vq , po - заданные для невозмущенной среды значения плотности, составляющих скорости и давление соответственно. Распределение давления выбрано так, чтобы скорость звука была постоянной и равной с = ^[у . Скорость течения принимается нулевой, vq = [0,0,0]т ; плотность и давление в невозмущенной среде полагаются равными р0 = 1, До = 1 • Расчетная область имеет размеры LX=LV=%. Границы области считаются открытыми, что означает, что возмущения могут свободно выходить из расчетной области.

На рис. 1 приведены результаты расчетов на сетке 20 х 20 ячеек при значении числа Куранта 0.2. Показан профиль решения вдоль средней линии области течения у = 7L_v/2 в момент времени t = 2 .

Высокий уровень диссипации, присущий численному потоку LF приводит к значительному «размыванию» решения, получаемого при помощи метода конечных объемов (FVM), см. рис. 1, а. В то же время, кусочно-линейная аппроксимация приводит к получению решения, хорошо согласующегося с аналитическим. Менее диссипативный поток HLLC (рис. 1, Ь) обеспечивает несколько более высокое качество решения методом контрольного объема, однако при использовании кусочно-линейных базисных функций эффект от применения потока HLLC практически не заметен. Вычислительные эксперименты показывают, что численная схема остается устойчивой при величине числа Куранта не более 0.2.

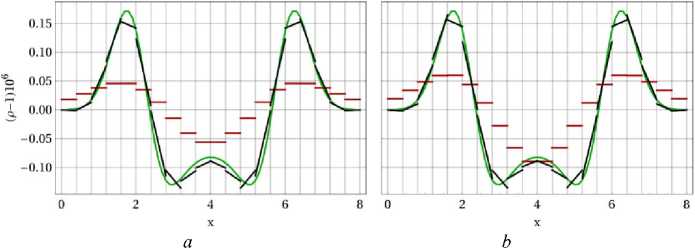
Рис. 1. Распространение акустической волны; сетка 20x20 ячеек, число Куранта Со = 0.2 . показан график плотности вдоль средней линии по направлению оси Ох в момент времени t = 2.0: а- для численного потока LF, b - для численного потока HLLC. Черные линии - численное решение с тремя базисными функциями (кусочнолинейная аппроксимация), красные линии - решение методом конечного объема (кусочно-постоянная аппроксимация), зеленая линия - точное аналитическое решение Fig. 1. Propagation of acoustic pulse, mesh 20 x 20 cells, Co = 0.2 , density plot along the center line in X -direction, t = 2.0: (a) LF numerical flux, (b) HLLC numerical flux. Black line is the numerical solution with 3 basis functions (piecewise-linear solution representation), red line is FVM solution (pieciwise-constant solution representation), green line is the analytical solution

• 4.2    Задача Сода

Другая группа тестов основана на задаче Сода, решение которой содержит три основных типа разрывов: ударную волну, волну разрежения и контактный разрыв. Качество разрешения этих разрывов зависит от чувствительности используемого индикатора проблемных ячеек, а также от выбора алгоритма монотонизации и используемого численного потока.

Первый тестовый расчет соответствует одноосному распространению волн: предполагается, что решение распространяется вдоль оси Ох, тогда как в направлении оси Оу расчетная область состоит лишь из одной ячейки.

Начальные условия для данной задачи имеют вид

(p,u,v,w,p) =

(1,0,0,0,1), х <0.5,

(0.125,0,0,0,0.1), .v > 0.5.

Результаты расчетов получены для сетки, состоящей из 100 ячеек в напрвлении оси Ох при значении числа Куранта 0.1. Расчет выполнялся до момента времени t = 0.2 . Параметры расчета соответствуют таковым применительно к решению одномерной задачи [7].

Первая группа результатов (рис. 2) представляет численные решения, полученные с использованием индикатора проблемных ячеек KXRCF при использовании различных численных потоков и лимитеров. На рис. 2, а представлено численное решение задачи Сода полученное с использованием MUSCL-лимитера и численного потока LF. Данные сравнительно простые алгоритмы позволяют достигать хорошего качества решения в смысле монотонности, однако обеспечивают низкое качество разрешения разрывов: около 6 ячеек на фронт ударной волны и 10-12 ячеек на контактном разрыве. Также наблюдается потеря точности решения внутри волны разрежения и образование выраженного «горба» перед ее фронтом.

Использование более точного численного потока HLLC позволяет повысить качество решения в целом (рис. 2, Ь\ При этом несколько повышается точность моделирования волны разрежения и качество воспроизведения решения в областях его гладкости. Тем не менее, число ячеек, приходящихся на разрывы, остается сравнительно большим.

Изменения качества численного решения становятся более существенными при замене MUSCL-лимитера на лимитер WENO S (рис. 3, 4). Этот лимитер обеспечивает размазывание ударной волны на две ячейки, контактного разрыва - на пять ячеек даже при применении такого существенно диссипативного потока, как поток LF, и в то же время сохраняет компактность шаблона аппроксимации, присущую разрывному методу Галеркина, и использует данные только с соседних (рис. 3, а). Согласно идее WENO-реконструкции, паразитные осцилляции полностью не исключаются, но должны убывать по амплитуде при измельчении сетки. Можно видеть эти осцилляции на гладких участках решения между разрывами. Использование 292

более точного численного потока, например, HLL или HLLC, позволяет дополнительно улучшить качество приближенного решения (рис. 3, Ь, 4, а).

Предыдущие результаты были получены при помощи первого варианта реализации методики WENOS, использующей одновременно 4 соседних ячейки. Указанный выше подход с использованием полусуммы результатов квазиодномерного лимитирования численного решения вдоль каждой из осей оказывается менее эффективен в силу больших вычислительных затрат при меньшей разрешающей способности на разрывах по сравнению с первым вариантом.

Заметим, что монотонность решения существенно зависит от используемого индикатора проблемных ячеек. На рис. 4, b показаны результаты расчетов, полученные при применении лимитера на всех ячейках. В этом случае лимитер WENOS дает более качественное решение, подавляя «горб» в голове волны разрежения и практически убирая осцилляции в области гладкости решения. В то же время, использование индикации проблемных ячеек существенно снижает вычислительную стоимость лимитирования. Индикатор KXRCF является популярным в силу относительно простоты адаптации к многомерным задачам.

Следующий тест - задача Сода с начальным положением фронта на диагонали х + у = 1 расчетной области - единичного квадрата. Начальные условия взяты следующим образом:

(AM,v,w,jo) =

(1,0,0,0,1), х + у<1, (0.125,0,0,0,0.1), х + у>1.

Численное решение на рис. 5 получено в момент времени t = 0.2 на сетке 40 х 40 и с соотношением временного и пространственного шага 0.1. Для расчетов выбран численный поток НЕЕС. В качестве граничных условий взяты условия свободного вытекания. Такие граничные условия приводят к возникновению искусственных отраженных волн в окрестности углов расчетной области. В связи с этим сравнение численного и точного решений произведено вдоль линии х = у, где влияние таких волн пренебрежимо мало.

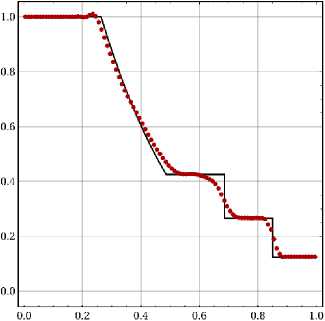
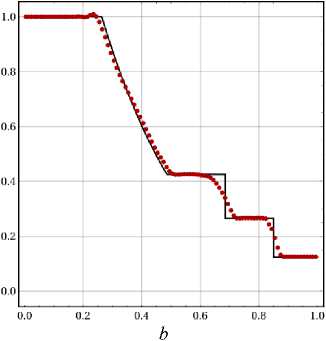
Puc. 2: Задача Сода, распределение плотности в момент времени t = 0.2/ точное (черная кривая) и численное (красные точки) решения. Расчеты с лимитером MUSCL, индикатором KXRCF и численными потоками LF (а) и HLLC (Ь)

Fig. 2: The Sod problem, density’ distribution in the final moment of time: the analytical solution (black line) and numerical solution (red dots). The calculation with MUSCL approach, KXRCF indicator and numerical fluxes LF (a) and HLLC (b)

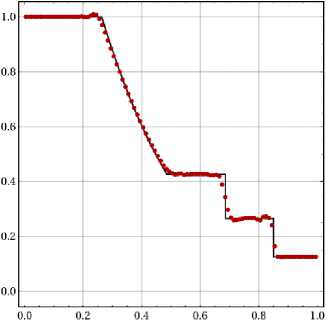
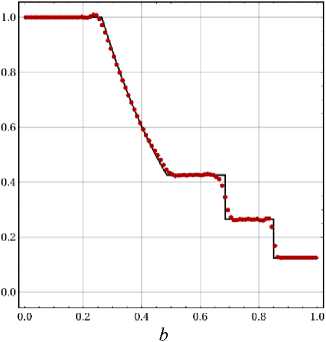
Puc. 3: Задача Coda, распреЬеление плотности в момент времени t = 0.2/ точное (черная кривая) и численное (красные точки) решения. Расчеты с индикатором KXRCF, лимитером WENOS и численными потоками LF (а) и HLLC (b)

Fig. 3: The Sod problem, density’ distribution in the final moment of time: the analytical solution (black line) and numerical solution (red dots). The calculation with KXRCF indicator, WENOS limiter and numerical fluxes LF (a) and HLL (b)

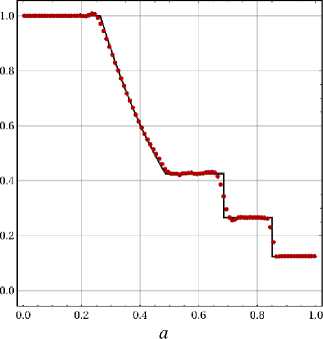
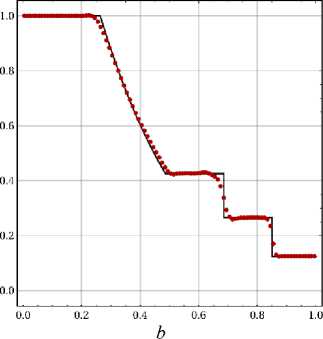
Рис. 4: Задача Сода, распределение плотности в момент времени t = 0.2/ точное (черная кривая) и численное (красные точки) решения. Расчеты с лимитером WENOS численным потоком HLLC и индикатором KXRCF (а) и лимитированием по всем ячейкам (Ь)

Fig. 4: The Sod problem. The density distribution in the final moment of time: the analytical solution (black line) and numerical solution (red dots). The calculation with WENOS limiter and numerical fluxes HLLC. Two situations: KXRCF indicator (a) and with limitation all the cells (b)

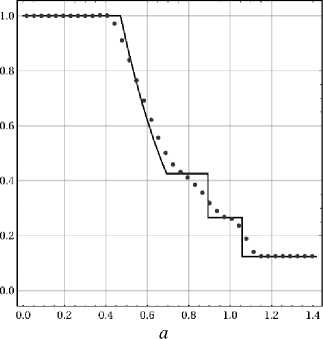
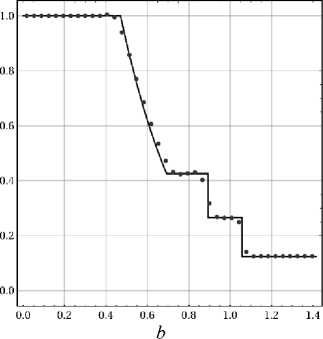
Puc. 5. Задача Сода, распределение плотности вдоль линии х = у в момент времени t = 0.2/ точное (черная кривая) и численное (красные точки) решения. Расчеты с численным потоком HLLC и лимитерами MUSCL (а) и WENO S (b)

Fig. 5. The Sod problem, density’ distribution along the line x = у in the final moment of time: the analytical solution (black line) and numerical solution (red dots). The calculation with numerical flux HLLC and limiters MUSCL (a) and WENOS (b)

Численная схема с лимитером MUSCL имеет высокую численную вязкость (рис. 5, а). Напротив, лимитер WENOS позволяет получить численное решение более приемлемого качества (рис 5, Ь\ Разрешение разрывов соответствует полученным выше результатам для одноосного распространения волн.

5.    Заключение

Рассмотрена реализация алгоритма RKDG метода для решения двумерных задач газовой динамики на структурированных прямоугольных сетках с использованием линейных базисных функций. В разработанном авторами статьи программном комплексе использованы численные потоки Лакса -Фридрихса, HLL и HLLC, индикатор проблемных ячеек KXRCF и лимитеры WENOS и MUSCL. Численное решение тестовой задачи о распространении акустического возмущения хорошо согласуется с аналитическим решением даже на довольно грубой сетке, в отличие от результата применения существенно более диссипативного метода конечных объемов. Эффективность реализации двух рассмотренных лимитеров протестирована на задаче Сода в квазиодномерной постановке. Численная схема с лимитером MUSCL имеет более высокую численную вязкость на разрывах, чем с лимитером WENO S. Показано, что использованный индикатор KXRCF может не определять некоторые немонотонности численного решения.

Работа выполнена при частичной финансовой поддержке РФФИ (проекты 18-01-00252 и 16-02-00656).