Математическое моделирование физико-химических процессов в пористых средах при решении задач создания нанокомпозиционных материалов и влагонаполнения

П онятие «пористая среда» (ПС), как правило, соответствует некоторому объему пространства, в котором присутствуют как твердая субстанция, называемая обычно матрицей или твердой фазой, так и пустоты – поры, заполненные воздухом, газом или жидкостью разной природы. Основными характеристиками ПС являются: ее пористость – отношение объема пор к общему объему области – и реакционная поверхность – площадь твердой фазы в единичном объеме пористой среды. При решении научных и технологических задач, предполагающих исследование процессов в пористых средах, используются как свойства составляющих их пористых материалов, так и механизмы физико-химических гомогенных реакций в объеме и гетерогенных – на поверхности раздела фаз.

В большинстве случаев для решения различных научных, материаловедческих, технологических и инженерных задач требуются экспериментальные исследования макрокинетики процессов и разработка на их основе научных и технологических рекомендаций по использованию процессов в пористых материалах. Однако сложность и трудоемкость системных экспериментальных исследований процессов в ПС определяют необходимость моделирования, в частности, математического моделирования физико-химических реакций в пористых материалах. Математическое моделирование позволяет не только выявить и исследовать определяющие физико-химические процессы в порах и на твердой фазе пористой среды, но и решать задачи по оптимизации и оптимальному управлению процессами посредством выбора наиболее благоприятных условий и режимов решения технологических задач.

Целью работы является математическое моделирование процессов: 1) создания композиционных и нанокомпозиционных материалов; 2) влагопогло-щения в пористых материалах; 3) увлажнения пористых материалов.

Для создания композиционных материалов в различных отраслях промышленности (авиационной, космической, машиностроительной, медицинской, химической и др.) широко используются углеродные волокнистые материалы (УВМ), представляющие собой объемно-пористую среду с различными технологическими свойствами. Использование УВМ для перечисленных задач связано с осаждением на поверхность составляющих их волокон металлов, сплавов или их соединений. Одним из перспективных методов для этого является электрохимический, позволяющий управлять токовым и гидродинамическим режимами электролиза, составом электролита, конструкционным оформлением электродной системы. При этом решается задача нанесения равномерного осадка металла или покрытия УВМ металлом с определенным профилем по толщине материала. Очевидно, что эффективным решением является использование методов математического моделирования и оптимизации процессов осаждения металлов в проточном трехмерном электроде (ПТЭ) на основе УВМ.

Задачи влагопоглощения и увлажнения пористых материалов возникают при реализации различных технологических процессов в материаловедении, в промышленной и строительной экологии. Как и в предыдущем случае, эффективными методами расчета оптимальных условий физико-химических процессов увлажнения-влагопоглощения являются методы математического моделирования процессов в пористых средах, опирающиеся на физикохимическую теорию пористых сред, современные численные методы и вычислительные технологии.

Задача математического моделирования распределения относительной влажности кондиционированного воздуха в пористой среде, в частности, в объеме компактно сформированного текстильного полуфабриката, является актуальной как для разработки теоретических положений, так и для совершенствования технологических процессов влаго-поглощения-увлажнения материалов. Значимость решения научных и технологических задач увлажнения – влагопоглощения различных материалов определяется необходимостью улучшения физикомеханических свойств увлажняемых волокон, таких как разрывность, упругость и прочее. Как отмечается в литературных источниках, исследование процессов влагопоглощения-увлажнения, в том числе и методами математического моделирования, способствует развитию теоретических положений и позволяет определять технологические параметры, обеспечивающие наибольшую эффективность процесса [1–7].

МАТЕРИАЛЫ И МЕТОДЫ

Математические модели физико-химических процессов в объемно-пористых псевдогомогенных средах

При построении математических моделей процессов в ПС будем использовать идею академика Б.Я. Зельдовича [8], когда пористая среда представляется как псевдооднородная, в каждом элементарном объеме которой протекает кинетическая реакция, соответствующая определенному физикохимическому процессу. Естественно, кинетические и другие параметры, например, такие как коэффициент диффузии, константа скорости адсорбции, удельная реакционная поверхность, коэффициент пористости и прочие при таком подходе должны иметь некоторые усредненные значения. При этом,

СТРОИТЕЛЬНОЕ МАТЕРИАЛОВЕДЕНИЕ

исходя из теоретических представлений об описании электродных, диффузионных и гидродинамических процессов в пористых средах, приведем математические постановки в виде краевых задач для систем дифференциальных уравнений и методы их решений для конкретных технологических задач.

Электрохимическая металлизация углеграфитовых волокнистых материалов

При создании композитных и нанокомпозитных материалов на основе УВМ необходима организация процесса нанесения электрохимического покрытия твердой фазы – пористого материала, обеспечивающего равномерный осадок на углеграфитовых нитях, составляющих проточный трехмерный электрод (ПТЭ), или осадок определенного профиля по толщине электрода. Для определения наиболее благоприятных условий электроосаждения использование математического моделирования позволяет ставить и решать задачи оптимизации и оптимального управления процессом металлизации [9].

В большинстве электрохимических систем реализуются теоретические законы миграции и конвекции заряженных частиц, описываемые системами дифференциальных уравнений в частных производных [10, 11]:

а также зависимость концентрации металла в объеме ПТЭ от времени меняется медленно в процессе осаждения и, в первом приближении, этими изменениями можно пренебречь. В таких условиях, в соответствии с правилами построения математических моделей процессов в ПТЭ, описанными, например, в работе [9], в конечном итоге дифференциальное соотношение (1) может быть преобразовано к следующей системе обыкновенных дифференциальных и алгебраических уравнений:

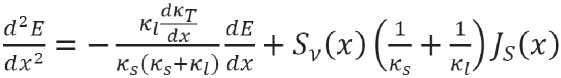
dC dx

—JsM

vzFJ5V '

с граничными условиями:

c(o) = co, ^(0) = ^/, ^(Ц = ^у, (4)

JM =jo

ехрОоиР^Е-ф^/КП^ехр^а-А^РОЕ-ф^ l+;₀ ехр(агР(Е-ф_к)/КТ)/гРК_тС

, (5)

^ = -Ч.^ЕС^Е + C^ , dt

где z_i , C_i , u_i – заряд, концентрация и подвижность i -го электроактивного компонента в псевдогомоген-ной среде; V E – градиент потенциала электрического поля; v – вектор скорости конвективного переноса раствора; t – текущее время процесса; F – число Фарадея, 7 • – дивергенция вектора.

Система дифференциальных уравнений (1) может быть преобразована с учетом псевдогомогенности среды, когда в каждой точке электродного пространства протекает реакция осаждения ионов металла на твердой фазе среды и, как следствие, не наблюдается электронейтральность раствора, присущая для гомогенных электрохимических систем при отсутствии реакций в объеме электролита. Это влечет за собой неравенство нулю производных от концентраций электроактивных веществ (ионов осаждающихся металлов) в любой точке с координатой x по толщине ПТЭ, ∂ C_i /∂ x ≠ 0. Учтем также, что для большинства задач металлизации УВМ достаточно рассмотреть электролит с одним компонентом – металлом покрытия, i = 1, а также случай, когда процесс металлизации можно моделировать одномерным стационарным дифференциальным уравнением, полагая, что во всех сечениях ПТЭ горизонтальными и вертикальными плоскостями происходят одни и те же электрохимические процессы,

где J – габаритная плотность тока, подаваемого на ПТЭ; S_v – удельная реакционная поверхность; C ₀ – концентрация металла на входе в электрод; κ _s , κ_l – удельные электропроводности твердой и жидкой фаз, j ₀, α, φ_R – соответственно плотность тока обмена, коэффициент переноса и равновесный потенциал электрохимической реакции; R – универсальная газовая постоянная; T – абсолютная температура процесса; K_m – коэффициент массопереноса.

В зависимости от выбранных режимов нанесения металлического осадка на УВМ, некоторые электрохимические параметры процесса и системы могут быть зависимы как от времени процесса, так и от координаты по толщине электрода. Это такие величины, как удельная электропроводность твердой фазы системы – углеграфитового волокнистого материала, удельной реакционной поверхности и коэффициента пористости материала электрода. Методы расчета перечисленных динамических параметров разработаны нами и опубликованы, например, в монографии [11].

Относительно удельной реакционной поверхности необходимо особо заметить следующее. Зависимость S_v = S_v ( x ), рассматриваемая как функция от координаты по толщине электрода, может быть выбрана в качестве управляющего воздействия при постановке задачи оптимального управления металлизацией УВМ. Это обусловлено, во-первых, существенным влиянием величины S_v на результирующие показатели процесса, такие как равномерность распределения осадка или общее количество осажденного металла и, во-вторых, возможностью обеспечить необходимую удельную поверхность ПТЭ в раз-

СТРОИТЕЛЬНОЕ МАТЕРИАЛОВЕДЕНИЕ личных вертикальных сечениях электрода за счет искусственного сжатия-растяжения материала катода (УВМ) [9]. При таком подходе задача (2)–(5) может быть преобразована к виду, необходимому для реализации принципа максимума Л.С. Понтрягина [12, 13], применение которого позволяет рассчитывать наиболее эффективное, по заданному критерию равномерности, распределение Sv(x).

Увлажнение пористого материала влажным воздухом

При построении математической модели процесса увлажнения пористого материала кондиционированным воздушным потоком с учетом принятых ранее допущений будем считать, что в каждом элементарном объеме пористого пространства, принимаемом за точку в объеме среды, происходит реакция адсорбции влаги, которая имеет свои микроскопические закономерности.

Кроме того, допустим, что температура воздуха во всех точках технологической зоны процесса увлажнения материала одинакова. Это естественно в случае, когда подаваемый кондиционированный воздух не меняет температуру с течением времени, что часто реализуется в рамках технологических требований реальных процессов увлажнения пористых материалов. В случае если перепады температур в различных областях увлажняемого материала существенны, предлагаемый подход к математическому описанию изучаемого процесса не меняется, добавляются уравнения теплопередачи и сохранения тепла, что приводит к усложнению математической модели, но не меняет принципов моделирования и расчета.

Очевидно, важнейшими движущими силами проникновения влажного воздуха к внутренним, труднодоступным участкам пористого материала являются принудительный поток воздуха и диффузионный механизм. При этом учет скорости микроскопической реакции увлажнения среды должен производиться в соответствии с теорией и практикой зависимости влагосодержания материала от относительной влажности воздуха и теплопроводности среды.

Исходя из закона сохранения вещества, в каждой точке рассматриваемой среды изменение влажности ϕ во времени t подчиняется уравнению [14]:

• "^ - ^-^*Ucon + Jdif) + jsou . (6)

Здесь jcon = ϕ•w – принудительный поток воздуха, обусловленный наличием начальной скорости подачи воздуха в пористую среду; w = (w1,w2,w3) – вектор скорости движения кондиционированного воздуха сквозь пористую среду; jdif = D7(ϕ) – поток, обусловленный диффузией влаги; D – усредненный коэффициент диффузии; jsou = kFS f(ϕ) – от- рицательный источник, вызванный потерей влаги из увлажняющего воздуха за счет адсорбции влаги в каждой точке объема псевдооднородной среды; k – константа скорости адсорбции на единицу поверхности; FS – удельная поверхность единицы объема пористой среды.

Поскольку рассматривается псевдооднородная модель пористой среды, то значение D , естественно, не является истинным коэффициентом диффузии влаги в однородной среде, а представляет собой некоторый рабочий параметр, позволяющий с определенной степенью точности описывать процесс диффузии влаги в пористой среде.

Плотность источника поглощения влаги из увлажняющего воздуха f ( ϕ ), очевидно, зависит от механизма увлажнения материала и определяется формой связи влаги с влажным материалом [7, 14]. Для описания такого механизма существует множество моделей, например [3], которые описывают частные физико-химические процессы и неудобны при математическом моделировании. Нами разработан оригинальный подход к описанию кривой адсорбции влаги в виде функциональной зависимости f ( ϕ ), представленный ниже.

Моделирование кривой адсорбции влаги

Адсорбционная кривая в рассматриваемом случае представляет зависимость равновесной влажности волокон W ( x ) в любой точке псевдогомогенной среды от относительной влажности воздуха ϕ ( x ). Экспериментально полученные адсорбционные кривые изображены на рис. 1.

Анализ вида кривых, представленных на рис. 1, позволяет выделить для описания экспериментальной зависимости аналитической функцией два участка: при 0 <  ϕ ( x ) <  ϕ_c (60–70%) – участок выпуклостью вниз и при ϕ_c <  ϕ ( x ) < 100% – участок выпуклостью вверх; ϕ_c – некоторая усредненная константа, имеющая определенное значение для каждого вида пористого материала. На каждом из выделенных участков установим аналитическую зависимость равновесного влагосодержания от влажности воздушного потока , при этом используем следующие рассуждения.

На первом участке кривой скорость роста объема адсорбированной влаги пропорциональна как ее значению при данной влажности W , так и разности ( W_M – W ), где W_M – предельное влагосодержа-ние пористого материала. Это обусловлено тем, что, во-первых, осаженные молекулы влаги создают дополнительные центры адсорбции, что способствует ускорению увлажнения, а во-вторых, возможности роста W до точки насыщения W_M . Итогом приведенных рассуждений является уравнение:

dW / dϕ = kW ( W_M – W ),

СТРОИТЕЛЬНОЕ МАТЕРИАЛОВЕДЕНИЕ

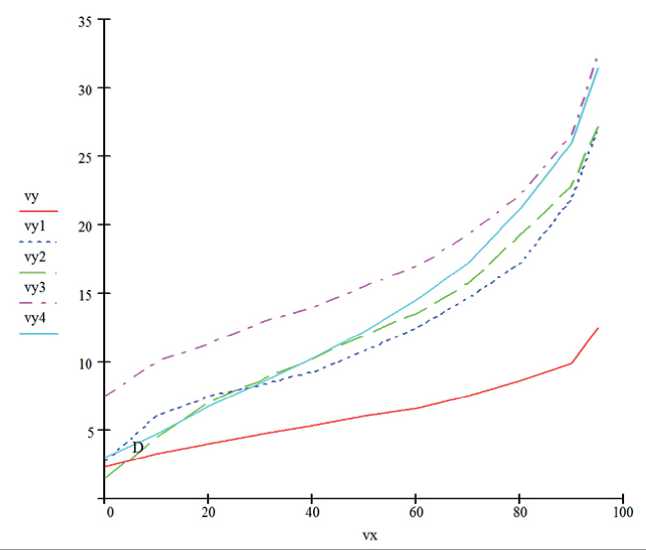
Рис. 1. Зависимость равновесной влажности волокон: vy4 – вискоза, y3 – пряжа, vy2 – шерсть, vy1 – ровница, vy – капрон

где k – некоторый коэффициент пропорциональности.

Зная начальную равновесную влажность волокон W_n , нетрудно получить решение этого уравнения:

w =

Wn

1+(И^_г/И/_м — l)*exp(— кф) ^.

На втором участке изменения ϕ при ϕ ≥ ϕ_c механизм влагонаполнения капилярнопористой среды имеет мономолекулярный, а затем и капиллярный характер [13], что определяет экспоненциальный рост W при возрастании ϕ :

W = k ₂• exp ( k ₁ ( ϕ – ϕ_c )), (8)

пористого материала. Объединение кривых (7) и (8) приводит к описанию зависимости W от ϕ в виде алгебраической функции

W = k₂ ехр(к^ф - 0J) + 7—7-77^7------. (9)

.()

Соответствующие данным рис. 1 теоретические и экспериментальные кривые приведены на рис. 2.

Параметры кривых (9), рассчитанные по методу наименьших квадратов, приведены в табл. 1.

Математическая модель распределения влажности в объеме пористой среды

Уравнение (6) с учетом представлений (7), (8) в развернутом виде выглядит следующим образом:

dt     V¹ dx ^W2 dy^Ws dz)    \dx² dy² dz²)    s/(0). (10)

Будем считать также, что поток кондиционированного воздуха через границу пористой среды позволяет упростить уравнение (10) до одномерного. Это возможно, например, когда линии движения воздуха, проходящего через плоскую границу пористой среды, параллельны или когда уравнение (10) можно записать в цилиндрических или сферических координатах, что часто реализуется в реальных технологиях увлажнения. Сделанные предположения не ограничивают общности математической модели, но позволяют избежать громоздких преобразований при описании решения задачи.

В рамках принятых допущений уравнение (10) преобразуется к виду:

^Ф         d-ф • dw d ф у p г , ч /11 \

Tt ⁼ -^Tx" *Tx"^D^^^k^W . (11)

где k ₁, k ₂ и ϕ_c – некоторые эффективные параметры, значение которых можно определить методом наименьших квадратов для каждого конкретного

Начальное условие для задачи (10) очевидно:

ϕ (0, x ) = ϕ ₀.

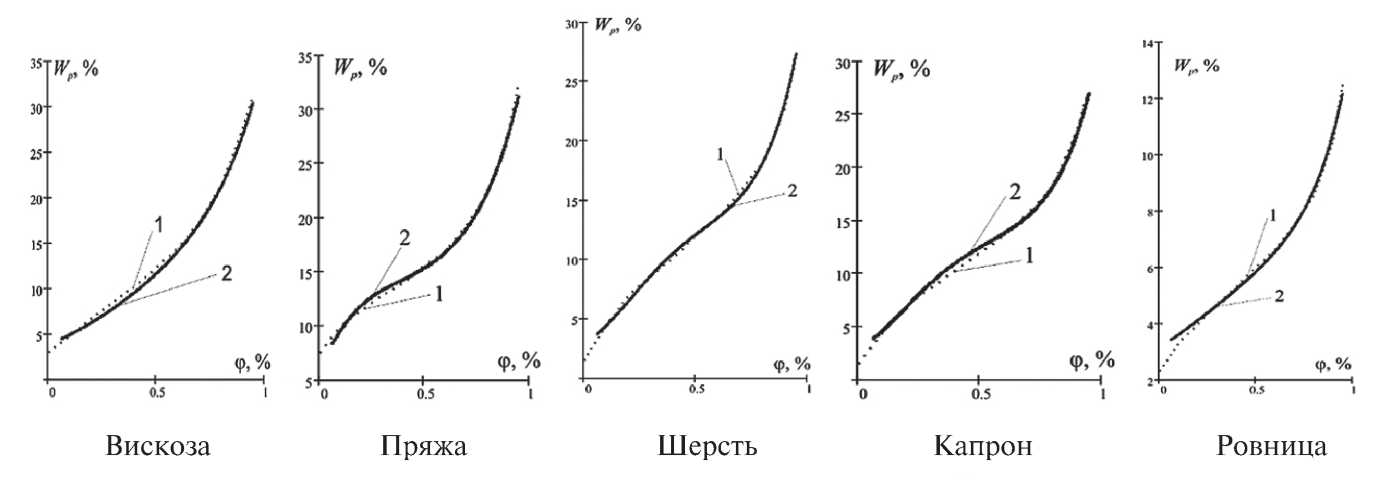
Рис. 2. Адсорбционные кривые: 1 – экспериментальные, 2 – расчетные

СТРОИТЕЛЬНОЕ МАТЕРИАЛОВЕДЕНИЕ

Таблица 1

Вид материала	W n	W	k 2	k 1	k	ϕc	S 2
Вискоза	14,9	3,5	3	4,4	3,3	0,55	2,5
Пряжа	13	6	3	4,5	10	0,55	1,8
Шерсть	13	2,7	2	6,6	6,5	0,65	1,9
Ровница	13	2,7	2	6,5	7	0,65	2,4
Капрон	8,5	31	0,9	5,95	23	0,66	0,84

Очевидно также, что в точке x = 0 (на границе пористой среды – поверхности), через которую осуществляется увлажнение, влажность соответствует влажности подаваемого в технологическую зону кондиционированного воздуха - ϕ ₁:

ϕ ( t ,0) = ϕ ₁. (13)

Для решения задачи (11)–(13) необходимо знать граничное условие для производной dϕ (0)/ dx в точке x = 0. Выделим элементарный объем в пористой среде единичной площади сечения и малой толщины V_m и рассмотрим изменение влагосодержания воздуха при прохождении его сквозь пористую среду заданного объема.

Относительная влажность воздуха в этом объеме ϕ ( x ) будет меняться по мере движения сквозь среду. Так, после прохода в толщу среды на расстояние ∆ _x влажность воздуха изменится до Φ _∆ за счет сорбции влаги, следовательно,

ϕ0–ϕ∆ = (Qp0–Qp∆)/Qmax, где Qp0,Qp∆ – количество водяного пара в единице объема влажного воздуха, соответственно, до и после увлажнения объема Vm пористой среды; Qmax – максимальное количество водяного пара в единице объема влажного воздуха. Следовательно, величина Vmax (ϕ0–ϕ∆ )•Vm/Ve равна количеству влаги, адсорбированной в порах среды объема Vm (Ve – единичный объем).

В каждой точке пористой среды влага осаждается согласно закону адсорбции, то есть кривой адсорбции, зависящей от физико-химических характеристик среды: W ( x ) = f ( ϕ ( x )), где W ( x ) – удельное влагосодержа-ние твердой составляющей пористой среды в точке х . Тогда количество адсорбированной влаги в объеме V_m среды будет равно ρS_m ∫₀^{∆ x} ( f ( ϕ ( x ))– W ₀) dx , где S_m – площадь, занятая твердой фазой, ρ – плотность пористого материала, W ₀ – удельное влагосодержание материала до увлажнения. Таким образом, получаем:

Q_max ( ϕ ₀– ϕ _∆)•( V_m / V_e ) = ρS_m ∫₀^{∆ x} ( f ( ϕ ( x ))– W ₀) dx .

Поделим обе части этого равенства на ∆x и перейдем к пределу при ∆x → 0. При этом логично положить, что после предельного перехода область Vm будет представлять собой часть единичной поверхности Sm, соответствующей площади пор, т.е. ε•Se, где ε – коэффициент пористости. А Sm, соответственно, является частью единичной поверхности, занятой твердой фазой среды, т.е. Sm = (1–ε)•Se. В результате получим условие для производной функции ϕ(x) в точке х = 0

^^-^.^(/■(фСО))- И/g). (14) сгл                c xmax

Таким образом, математическая модель увлажнения пористого материала путем воздействия продуваемого сквозь него влажного воздуха в общей постановке представляет собой нестационарную краевую задачу для уравнения в частных производных (10)–(14).

Исходя из реальных технологических условий рассматриваемого процесса увлажнения пористого материала, можно предположить, что в ряде случаев зависимость влажности волокон от времени в толщине среды можно считать кусочно-постоянной, так как изменение условий влагопоглощения происходит достаточно медленно, и, следовательно, для больших промежутков времени процесс распространения влаги в объеме пористой среды носит квази-стационарный характер, следовательно, в каждом из таких промежутков d_ϕ / d_t = 0, и уравнение (11) преобразуется к стационарной форме:

гх А ф      Аф , Aw .        ~ z lx

D — + w — + ф— = к ■ F_s ■ /(ф).

Ах2 Ах Ах           j x-rv

Уравнение (14) с начальными условиями (12), (14) представляет собой задачу Коши для обыкновенного дифференциального уравнения [15] и может быть решено различными способами, например, конечно-разностными.

В соответствии с представлением зависимости влажности волокон от времени в виде кусочно-постоянной функции, весь временной интервал процесса [0, T ] разбивается на подинтервалы точками T_i , и в каждом из подинтевалов [ T_i , T_{i +1}] используются специфические значения физических параметров пористой среды, коррекция которых необходима для каждого следующего подинтервала из-за изменения

СТРОИТЕЛЬНОЕ МАТЕРИАЛОВЕДЕНИЕ свойств материала в результате осаждения влаги объемом m на твердые волокна объема среды, их разбухание и, как следствие, увеличение радиуса волокон, что, в свою очередь, приводит к изменению пористости εm, реакционной поверхности среды FS,m и линейной скорости движения воздуха vm. Используя классические выражения для определения удельной реакционной поверхности волокнистого материала и ее пористости, а также измеряемого среднего радиуса волокна d и плотности увлажняющей жидкости ρ:

. (16)

Для проведения расчетов по уравнениям (12), (13), (15), (16) использовался метод Рунге-Кутта с автоматическим выбором шага интегрирования.

Влагопоглощение в известковых композитах

Проникновение влажного воздуха к внутренним участкам пористого композита осуществляется, в основном, диффузионным механизмом. Движение воздуха, обусловленное принудительной или естественной конвекцией, в данном случае, по-видимому, менее существенно из-за достаточной плотности материала и его пористости, составляющей менее 50% от общего объема материала.

В процессе влагопоглощения в каждой точке пористого пространства происходит реакция адсорбции влаги в соответствии с макро- и микроскопическими закономерностями. С учетом принятых ранее допущений, все кинетические параметры, в том числе и коэффициент диффузии, имеют усредненные значения, которые могут отличаться от истинных и определяются, как правило, экспериментально.

Механизм реакции влагопоглощения, как и в случае увлажнения пористого волокнистого материала, определяется кривой адсорбции влаги, конкретная форма которой зависит, естественно, от свойств материала. При этом математическая модель адсорбционной кривой, способ моделирования и все выводы относительно ее свойств, сделанные выше, справедливы и для рассматриваемого процесса.

Аналогично тому, как это было сделано для предыдущей задачи, получено математическое описание адсорбционных закономерностей влагопоглощения кривой зависимости равновесной влажности материала W от относительной влажности воздуха ϕ :

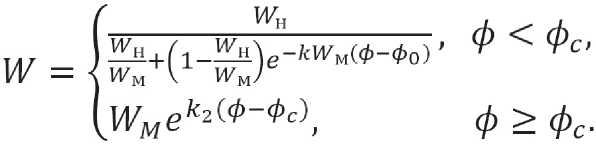
Здесь Wn – начальное значение влагосодержа-ния; WM – предельно возможное влагосодержание материала; k1, k2 и ϕc – рабочие параметры, значение которых определяется посредством математической обработки экспериментальных кривых с использованием метода наименьших квадратов.

Как и ранее, будем считать, что процесс влагопо-глощения, в первом приближении, является одномерным по пространственным координатам, и будем исследовать его закономерности, используя одномерную математическую модель.

Исходя из основного уравнения массоперено-са влаги в пористой среде (10), с учетом сделанных предположений и допущений, математическое описание процесса влагопоглощения может быть записано в следующем виде:

^ = D^-kSf№ . (18)

Здесь D – эффективный коэффициент диффузии; S – удельная поверхность единицы объема материала; k – некоторая константа; 0 ≤ x ≤ L , L – толщина пористого материала.

Решение уравнения (18) получено с использованием функции источника [16], при этом считается, что за пределами массива увлажняющегося материала x ≤ и x ≥ L , f ( x ) = 0:

. (19)

В случае, когда процесс увлажнения можно считать стационарным, уравнение (18) упрощается:

D^-kSf^ = 0. (20)

При значительных начальных показателях влажности воздуха ϕ ≥ ϕ_c можно рассматривать только вторую часть адсорбционной кривой (выпуклостью вверх)

kSf(ϕ) = WM e(k2 (ϕ-ϕc)), что позволяет записать уравнение для расчета влажности пористой среды в виде

D^-W_Me^k^"^ =0.

dx2 11

Будем считать известными значения влажности воздуха на границах раздела сред воздух – пористый материал: ϕ (0) = ϕ ₀, ϕ ( L ) = ϕ_L .

Решение дифференциального уравнения (21) затруднения не вызывает и представляет собой следующую систему алгебраических выражений:

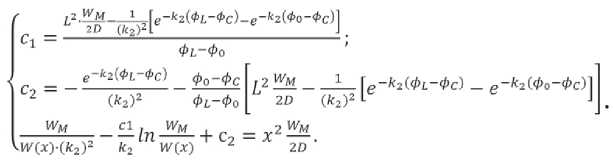
СТРОИТЕЛЬНОЕ МАТЕРИАЛОВЕДЕНИЕ

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Металлизация углеграфитовых волокон

С целью улучшения свойств композиционных и нанокомпозиционных материалов, создаваемых на основе УВМ, выполнено математическое моделирование и оптимизация процессов осаждения металлов в ПТЭ.

Верификация полученных моделей проводилась на основе экспериментальных исследований, выполненных В.К. Варенцовым [17, 18], предполагающих модификацию поверхностных свойств УВМ определенной марки с целью получения равномерных осадков при металлизации материала электрохимическим способом. При этом использовались тканые, нетканые и комбинированные углеродные материалы, отличающиеся удельной электропроводностью, реакционной поверхностью, пористостью [19–22]. Электрохимическую модификацию УВМ осуществляли в растворах различных электролитов анодной поляризацией, или последовательно катодной-анод-ной поляризацией, или их различной комбинацией. Показано, что в результате электрохимической обработки существенно улучшаются гидрофильные свойства материала, что обусловлено возрастанием количества поверхностных кислородсодержащих групп. Показано также, что электродная обработка УВМ в кислотных и щелочных растворах существенно влияет на адгезию осадка с поверхностью углеграфитового материала, что повышает эффективность процесса осаждения металла на УВМ [17, 18].

Опыт разработки технологических процессов электроизвлечения благородных и цветных металлов из промышленных растворов на УВМ показал, что осаждение металлов на предварительно электрохимически обработанные материалы позволяет рассчитывать оптимальные режимы электроосаждения, что дает возможность получить равномерно распределенные осадки металла по толщине электрода, улучшить структуру, морфологию и состав осадков, следовательно, и свойства композиционного материала (рис. 3).

В качестве иллюстрации работоспособности использования метода математического моделирования при решении задач по определению эффективных технологических режимов металлизации УВМ выбрана задача покрытия УВМ марки ВВП-66-95 гальваническим осадком серебра из сернокислого тиомочевинного раствора со следующими параметрами электрохимической системы: толщина электрода – 1 см; плотность тока – 0,2 А/м2, скорость протока раствора – 0,56 см/с; удельная поверхность – 255 см2/см3, удельная электропроводность – 0,03 См/см, пористость – 0,95; удельная электропроводность раствора – 0,1 См/см; время электролиза – 60 мин; состав электролита: H2SO4 – 0,5 моль/л, тиомочевина – 50 г/л, серебро – 76 мг/л. Результаты расчетов распределения металла по толщине ПТЭ по математической модели (2)–(5) и, для сравнения, экспериментальные данные распределения серебра представлены на рис. 4.

Особо отметим, что на поверхность волокон УВМ можно электролитически осаждать наноразмерные частички металлов, что позволяет получать плотные покрытия углеграфитовых волокон с заданным профилем. В качестве иллюстрации приведем фотографии морфологии осадков платины на углеграфитовые нити (рис. 5).

Соответствие представленных на рис. 4 экспериментальных и расчетных кривых распределения серебра по толщине ПТЭ с катодом из выбранного УВМ подтверждает эффективность использования приведенных математических моделей и алгоритмов расчетов, описанных выше и в других наших работах, например, [9, 11, 13 и др.] для проведения численных

Рис. 3. Микрофотографии осадков меди на исходном (а) и электрохимически модифицированном (б) УВМ

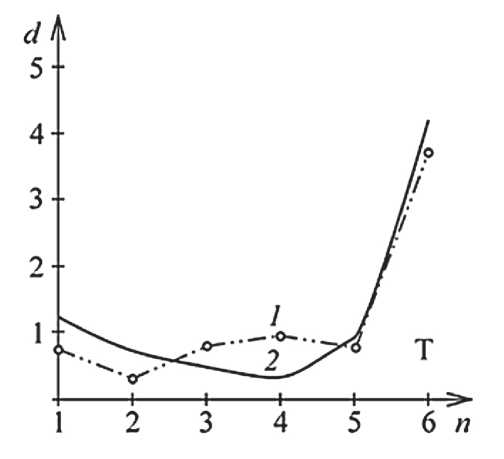
Рис. 4. Распределение осадка серебра по толщине электрода: 1 – эксперимент, 2 – расчет; d – отношение массы металла к массе УВМ; n – номер слоя; T – тыльная сторона электрода

СТРОИТЕЛЬНОЕ МАТЕРИАЛОВЕДЕНИЕ

Рис. 5. Микрофотографии осадков платины на УВМ

исследований процессов электроосаждения металлов при создании композиционных материалов с определенной морфологией и распределением осадка металла по поверхности волокон УВМ.

Следует отметить, что композиционные каталитические материалы на основе металлизированных платиной, серебром или их сплавом углеграфитовых волокон обеспечивают большую эффективность каталитических процессов окисления Се(III) в сернокислом растворе и окисления алифатических спиртов и альдегидов, а также сложных минерально-органических конденсатов в водных растворах [9, 11, 17]. Кроме того, такие катализаторы более удобны при их использовании в электрохимических реакторах различных конструкций, чем обычно используемый для этих целей активированный уголь.

Принудительное увлажнение компактно сформированных текстильных волокон

Представление увлажняемого материала как ограниченной пористой среды с распределенными по объему основными эффективными характеристиками позволило разработать математическую модель в виде краевой задачи математической физики, позволяющую рассчитывать распределение относительной влажности в объеме пористой среды при ее увлажнении влажным воздушным потоком.

В качестве иллюстрации работоспособности алгоритма на рис. 6 представлены результаты расчета изменения относительной влажности воздуха в объеме пористой среды при линейном законе изменения скорости движения увлажняющего воздуха w ( x ) = γx + µ .

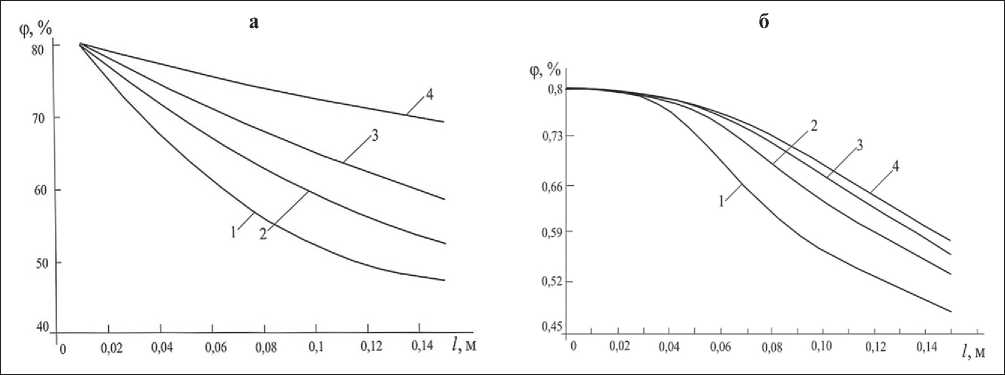
Рис. 6. Влияние начальной скорости потока воздуха v на распределение относительной влажности воздуха в объеме ПС с учетом линейного падения скорости в объеме среды: а – расчетные, б – экспериментальные кривые (1) – (4), соответственно, при v = 2, 4, 6, 8 м/с

СТРОИТЕЛЬНОЕ МАТЕРИАЛОВЕДЕНИЕ

Результаты расчетов и экспериментальные данные показывают их достаточную корреляцию. Как из расчетов, так и из экспериментов следует, что увеличение скорости движения увлажняющего воздуха способствует более равномерному распределению влаги в объеме увлажняемого материала. В то же время, очевидно, что увеличение интенсивности продувки влажным воздухом компактно сформированного текстильного материала требует либо увеличения мощности вентиляционного устройства, либо увеличения пористости материала. Даже такой простейший анализ показывает, что задача выбора технологического режима увлажнения может быть сформулирована в виде задачи оптимизации технологических параметров, влияющих на процесс увлажнения. Очевидно, что решение такой задачи невозможно без применения методов математического моделирования, оптимизации и расчета.

Влагопоглощение в пористых строительных материалах

На рис. 7 приведены расчетные (кривые) и экспериментальные (точки) данные влагопоглощения для двух пористых материалов: вспененного вермикулитового песка (1) и микросфер алюмосиликатной золы (2). Для численной реализации математической модели (22) использованы следующие значения параметров, найденные из экспериментальных адсорбционных кривых: k ₂ = 0,016, L = 2 см, ϕ (0) = 100, ϕ ( L ) = 50 и коэффициенты диффузии D ₁ = 7,67×10^–5 и D ₂ = 3,43×10^–5 см²/с для соответствующих кривых [23].

Расчетные и экспериментальные кривые, представленные на рис. 7а, показывают хорошее согласие и, следовательно, эффективность математической модели. Рис. 7б позволяет сделать вывод о достаточных затруднениях проникновения процесса в толщу материала даже при значительно продолжительном времени увлажнения. Очевидно, что задачу по определению значений таких параметров технологического процесса, как толщина материала, его пористость, время процесса и пр., обеспечивающих выполнение поставленной задачи увлажнения, наиболее эффективно решать посредством использования математической модели и численных расчетов.

Анализируя результаты расчетов, можно сделать вывод, что, по-видимому, величина коэффициента диффузии существенно влияет на процесс увлажнения пористого материала и может быть использована в качестве меры возможного влагосодержания композита.

Отметим, что для расчетов были разработаны компьютерные программы с использованием математической среды MathCAD и языка программирования Python с библиотеками/модулями Numpy, Scipy и Matplotlib.

ЗАКЛЮЧЕНИЕ

Таким образом, при выполнении исследований, приведенных в данной работе, использованы методы математического моделирования физико-химических процессов в пористых средах, основанные на теоретических представлениях об электродных, диффузионных, миграционных, адсорбционных процессах и их распределении в псевдогомогенных системах. На основе представления пористого мате-

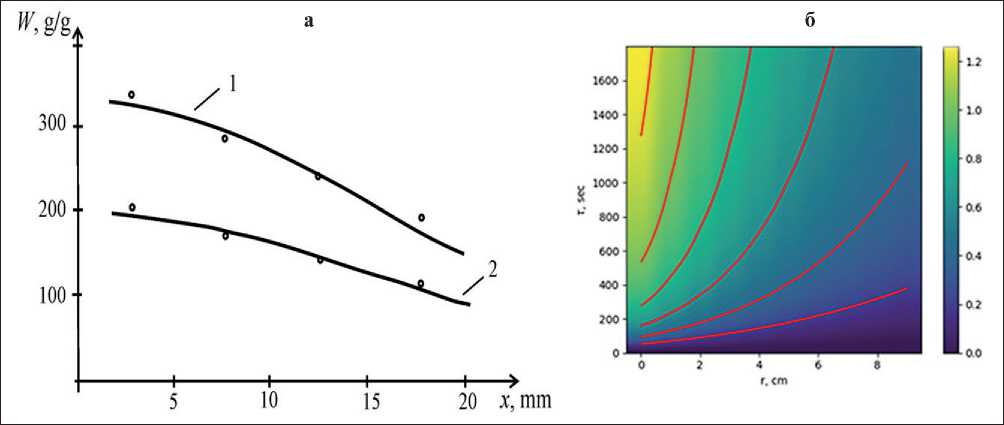
Рис. 7. Распределение содержания влаги в отделочном покрытии: а – расчет во вспученном вермикулитовом песке (кривая 1), в зольных микросферах алюмосиликата (2); точки – эксперимент; б – распределение влаги в объеме пористого материала с течением времени процесса

СТРОИТЕЛЬНОЕ МАТЕРИАЛОВЕДЕНИЕ риала в виде псевдооднородной среды, характеризуемой усредненными физическими и технологическими параметрами, а также на основе физико-математических описаний процессов в пористой среде построены математические модели и сформулированы краевые условия для расчета распределения физикохимических процессов в объеме рассматриваемой пористой среды при решении задач: 1) металлизации углеграфитового материала при создании на его основе композитных и нанокомпозитных материалов; 2) увлажнения волокнистого материала принудительным потоком кондиционированного воздуха; 3) поглощения влаги пористыми строительными материалами.

Имеющиеся в описании математических моделей некоторые характеристики ПС и кинетические параметры (например, удельная реакционная поверхность S_v , коэффициент пористости материала ε ) могут меняться как в течение процессов металлизации, так и влагопоглощения-увлажнения пористого материала, причем как в сторону увеличения, так и в сторону уменьшения своих значений. Изменения могут претерпеть и другие динамические характеристики процессов, например, линейная скорость движения электролита или увлажняющего воздуха сквозь пористую среду и др. Необходимые коррекционные выражения технологических и кинетических параметров в процессе физико-химических реакций в пористой среде приведены в каждом конкретном рассматриваемом случае.

В работе приводится математическое описание зависимости равновесной влажности пористого материала известкового композита от относительной влажности воздуха в виде кривых адсорбции влаги в исследуемом материале; построена математическая модель процесса увлажнения сухой строительной смеси на основе представления некоторого элементарного объема известкового композита в виде объемно-пористой среды с усредненными физикохимическими параметрами. Приведено сравнение теоретических и экспериментальных кривых, показано их хорошее соответствие.

Выполнены расчеты и проведен некоторый анализ влияния основных параметров процессов металлизации УВМ, увлажнения компактно сформированного текстильного материала и процесса влагопоглощения в известковом композите на распределения процессов в объеме пористой среды, составляющей реакционную псевдогомогенную область.

Представленные математические модели при заданных значениях параметров процессов, участвующих в соотношениях, определенных экспериментальным или расчетным путем, вполне адекватно описывают закономерности распределения физикохимических реакций в рассматриваемой пористой среде и могут быть использованы для теоретических исследований закономерностей, а также для расчета оптимальных значений технологических параметров рассматриваемых процессов.