Математическое моделирование формирования структуры при термообработке в элементах конструкций

Для описания изотермического распада аустенита в перлит использовано уравнение Авраами [1], а для бейнитного превращения более сложное уравнение, учитывающее ускорение хода превращения под нагрузкой и снижение предельной степени распада n (t)

V_Б ( τ ) = { 1 - exp [ - K_Б ( t ) ⋅ ( Ω ( σ_i ) ⋅ τ ) ^Б ] } ⋅ A ( t ) ⋅ B ( σ_i ) ⋅ V A^Б     (1)

где VБ, VAБ — удельные доли бейнита и аустенита, сохранившегося к началу бейнитного превращения соответственно; А — предельная степень превращения аустенита в бейнит при данной температуре. Коэффициенты КБ и nБ можно определить по изотермической диаграмме превращений переохлажденного аустенита. Зная для каждой температуры времена начала τНБ и конца превращения τКБ, а также соответствующие им объемные доли перлита VБН = 0,01 и VБК = 0,99, получаем n (t) = lg

ln(1 - V H ) /lg Th_ ln(1 - V k )     t .

, K ( t ) =

ln(1 — V_H ) ( τ н ) n

Подставляя в эти выражения τ Н^Б и τ К^Б , можно получить коэффициенты К s

и n Б для любой температуры бейнитной области.

Расчет структурного состава ведется шаговым методом. Плавная кривая изменения температуры в каждой точке валка заменяется ломаной, то есть принимается, что на каждом n-ом шаге по времени ∆τ n температура мгновен-

но меняется с t n-1 на t n и остается постоянной на данном шаге.

Согласно теории изокинетических реакций переход от изотермической

VБ (I,) =j 1 - exp - Кб (tn )[o(o,n-1 )(тБ + ^t, )]

nБ(tn)

^ VA A(tn) B(on-1)

кинетики распада аустенита к неизотермическим условиям осуществляется на основании правила аддитивности [4]. Уравнения для определения удельной доли бейнита на n-ом шаге имеют вид [4]

ТБ =         • n    ^(on-1) In ( 1 - v;-1/(Vf • A(t,) • B(on-1))' Пб(tn) _                   K (tn)                 J            (3) где Ω, В — эмпирические зависимости, учитывающие ускорение хода превращения и снижения предельной степени распада под нагрузкой; σi — интенсивность напряжений.

Выражения для расчета удельной доли перлита получаются из уравнений (1)–(3), при замене индекса «Б» на «П» и значениях V A^Б , А, В и Ω равных единице.

Для описания атермического мартенситного превращения использованы зависимости удельной доли от температуры, полученные в ходе дилатометрического исследования, проведенного в работе [2].

Таким образом, описанная методика расчета структурного состояния позволяет определять в каждой точке валка в каждый момент времени вектор удельных долей аустенита, перлита, бейнита и мартенсита соответственно — {V} = { VA, VП, VБ, VМ }. По данной методике была создана программа расчета на ПЭВМ. Исходными данными для программы являются: шаг по времени, температура и структурный состав на предыдущем шаге, температура на текущем шаге. Выходными данными — структурный состав, свободная деформация и суммарный коэффициент линейного расширения, учитывающий как чисто температурные деформации, так и деформации, связанные со структурными превращениями.

Адекватность математической модели структурных превращений аустенита подтверждалась посредством сравнения экспериментально полученной в работе [3] ТКД для стали 90ХФ с ТКД, прогнозируемой при использовании правила аддитивности. На рис. 1 штриховыми линиями изображены границы перлитной и бейнитной областей, определенные путем численного расчета, а сплошными линиями экспериментальные кривые. Следует отметить, что для хорошего согласования опытных и расчетных данных в бейнитной области использована методика, изложенная в работе [4], согласно которой производится смещения бейнитной области на ИТД вверх путем подстановки в уравнения, описывающие ИТД, скорректированного значения температуры tБ = aБ∙t (4) где t — температура, aБ = 0,75 — коэффициент, полученный в ходе численного эксперимента.

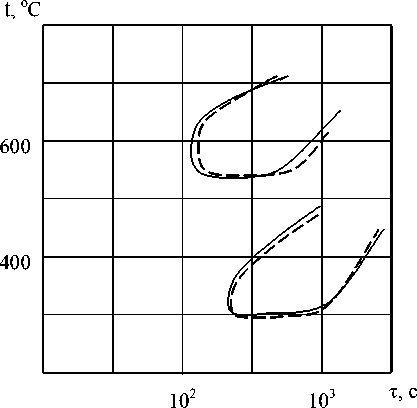
Рис. 1. Экспериментальные [5] (сплошные линии) и расчетные (штриховые линии) термокинетические диаграммы стали 90ХФ

Остановимся теперь на задании теплофизических характеристик, зависящих от структуры. Коэффициент теплопроводности гетерогенной структуры можно определить, исходя из правила смеси

λ = λ y ∙V A + λ α ∙(1-V A ) (5) где λ y , λ α — коэффициенты теплопроводности аустенита и продуктов его распада соответственно.

Использование для перлита, бейнита и мартенсита одной зависимости λα объясняется несущественным отличием их коэффициентов теплопроводности [5], обусловленного единой основой α — железа для этих структур. Коэффициент теплопроводности стали в аустенитном состоянии слабо зависит от химического состава, исходя из этого, λy принимался по усредненным значениям.

Коэффициент теплоемкости считался зависящим только от температуры и принимался по работе [4] в виде

C = 450 + 0,167∙t, Дж/кг·К

Тепловые выделения при различных структурных превращениях рассчитывались по следующей конечно-разностной формуле

S         ∆VS qV = ρ ⋅ LS ⋅ ∆τ где Ls — удельная теплота структурного превращения, Vs — объемная доля продукта распада.

Предполагая, что объемные деформации, связанные со структурными пре- вращениями, так же, как и чисто температурные, происходят изотропно, плотность можно определить по свободной деформации [4]

ρ = ρ0/(1 + εТ), где εТ — свободная деформация, зависящая от температуры и структуры; ρ0 = 7,8·103 кг/м3 — плотность инструментальной стали в перлитном состоянии при температуре 20оC [6].

Кроме отмеченного, вычисление структурного состояния стали в каждой конкретной точке элемента в каждый момент времени необходимо для расчета суммарного коэффициента линейного расширения, учитывающего как чисто температурные деформации, так и деформации, связанные с формированием другой кристаллической решетки при структурных превращениях. Этот коэффициент можно определить по следующей формуле

α n = (ε Tⁿ — ε T^n-1 )/∆t n                                          (6)

где ε Tⁿ , ε T^n-1_— свободные деформации на текущем и предыдущем шаге.

На основании правила смеси свободная деформация гетерогенной структуры ε T может быть определена по свободным деформациям составляющих структур пропорционально их удельным долям [4]

ε T = ε T^A V A + ε T^П V П + ε T^Б V Б + ε T^М V М , (7) где ε T^A , ε T^П , ε T^Б , ε T^{М —} свободные деформации аустенита, перлита, бейнита и мартенсита соответственно, которые можно определить по дилатограммам этих структур.

Принимая во внимание, что коэффициенты линейного расширения перлита, бейнита и мартенсита, имеющих в основе α -железо [5], должны отличаться незначительно, ε T^Б полагалась равной ε T^П , а зависимость для ε T^М получалась посредством смещения перлитной дилатограммы параллельно самой себе в точку со свободной деформацией мартенсита при 20 ^о С. Зависимости ε Т^А , ε Т^П , ε Т^М для стали 90ХФ принимались согласно работе [6], в которой было проведено дилатометрическое исследование валковой стали 90ХФ

ε_Т^А = 1,37 ⋅ 10 - ¹² t ² + 2,21 ⋅ 10 - ⁵ t - 8,18 ⋅ 10 - ³ ,

εТП =2,05⋅10-14t2+1,31⋅10-5t -2,61⋅10-4,               (8)εТМ=2,05⋅10-14t2+1,31⋅10-5t+1,03⋅10-3 .

При использовании численного метода расчета по температуре данного шага по формулам (8) можно рассчитать свободные деформации составляющих структур, а по выражению (7), зная структурный состав, свободную деформацию гетерогенной структуры. Далее по формуле (6) можно определить суммарный коэффициент линейного расширения.