Математическое моделирование характера распределения контактного давления между внутренней поверхностью конического уплотнителя и стенкой цилиндра

Постановка и решение задачи

Уплотнение цилиндрической поверхности трубы в ряде случаев приходится осуществлять уплотнительным элементом, имеющим форму усеченного конуса (рис. 1). Это происходит из-за разности наружных диаметров трубы и соединительной муфты, которая проходит через отверстия уплотнительного элемента, что приводит к увеличению зазора между внутренней поверхностью уплотнительного элемента и уплотняемой стенкой цилиндра. А это, в свою очередь, приводит к осложнению достижения герметичности поверхности цилиндра. Для достижения герметичности стенки цилиндра меньшей осевой нагрузкой и улучшения герметизирующей способности уплотнительного элемента он выполняется в форме усеченного конуса. При приложении осевой нагрузки усеченный конус, скользя наружной поверхностью по корпусу, сужается во внутрь, уменьшая при этом свой внутренней диаметр. Это приводит к более равномерной деформации внутренней цилиндрической поверхности уплотнительного элемента, что сильно влияет на характер распределения контактного давления между стенкой цилиндра и внутренней поверхностью уплотнителя.

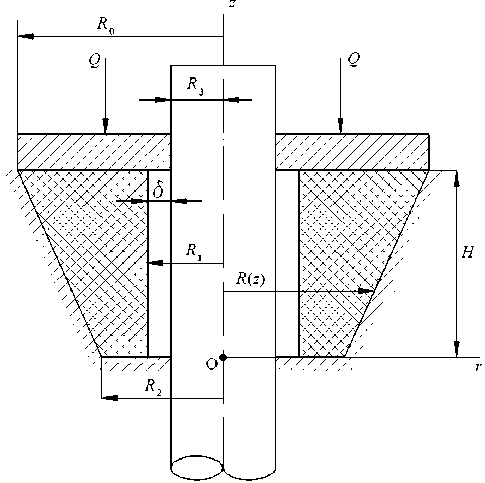
Рис. 1. Расчетная схема.

Изучению герметизации стенки трубы уплотнительным элементом имеющей форму усеченного конуса, посвящен ряд работ [1–10]. Однако в них не учтены краевые эффекты и сильно упрощена математическая модель расчета уплотнительной способности герметизирующего элемента. Поэтому исследование и изучение герметизирующей способности уплотнительного элемента, имеющего форму усеченного конуса, и на этой основе разработка эффективных мер для улучшения его герметизирующей способности имеет как практическое, так и научное значение.

Рассмотрим уплотнительный элемент, надетый на цилиндр с зазором 5 , упирающим конической наружной поверхностью к стенке корпуса (рис.1). Герметичность поверхности корпуса и стенки цилиндра достигается путем одностороннего осевого сжатия уплотнительного элемента. Решение задачи выполним в два этапа. Первый этап – сжатие уплотнительного элемента до соприкосновения его наружной поверхности со стенкой цилиндра, а второй – достижение герметичности.

Первый этап. Поскольку материал уплотнительного элемента является однородным, то в данной задаче его деформацию можно принять осесимметричной. Тогда можно принять и гипотезу плоских сечений и предположить, что осевая деформация уплотнительного элемента зависит только от координаты z в осевом направлении.

Начало координатной системы поместим в центре нижнего сечения уплотнительного элемента, координатную ось z направим вертикально вверх, а ось r – в сторону увеличения радиуса, как показано на рис.1.

С учетом вышепринятых допущений деформацию уплотнительного элемента w в осевом на- правлении можно принимать в виде w = f (z),                    (1)

где f ( z ) - неизвестная функция, зависящая от z и подлежащая определению [1, 6, 7].

Принимая материал уплотнительного элемента несжимаемым, будем иметь

1 s u) w = о ,           (2)

r dr    dz где u ( r, z ) - деформация уплотнителя в ради- альном направлении.

Из выражения (2) с учетом формулы (1) получаем

1 8(ur) = —f( z).(3)

r 9 r

Интегрируя выражение (3), получаем

u(r, z) = - rf (z) + —, где cо - постоянная интегрирования.

Граничное условие

Ц r = R ( z ) = ⁰ .

Тогда из выражения (4) с учетом граничного условия (5) получаем

1 u =

Г R iC i ) V ^r

- r I f' ( z ) .

Потенциальная энергия уплотнительного элемента после его деформации с учетом осесим-метричности будет иметь вид [1]

HR(z) r                   1     A           H , n = 4nGj j I £2 + Eg + £z2 + -/rz Irdrdz-JQ■ f (z)dz

0 R i ^{V                     2}     V              0

где H – высота, R ₁ , R ₂ – соответственно внутренний и наружный радиусы уплотнителя, Q – осевая нагрузка для поджатия уплотнителя до первого соприкосновения его внутренней поверхности со стенкой цилиндра, ε _r , ε_θ , ε _z и γ _rz – соответст-

x | 1   nz | ,      • nz f (z) = c, I , — cos----I + c, sin----

’ I 2 H J 2    2 H

+ c ³ z ,   (14)

H

где

c ₁ , c ₂ , c ₃

–

Постоянное

постоянные.

c ₃ определяется

из граничного

венно радиальная, тангенциальная, осевая и сдвиговая деформации [1, 11].

условия (13)

ε _r

д u

5 r

u e9 =   ’ ^z

r

d w

, γ _rz 5 z

c 3

—

2 δ H R ₁ π

.

R ₂ ² — R , ²   2 ²

Тогда из выражения (7) с учетом формул (1), (6) и (8) получаем:

Подставим выражение (14)

в уравнение

(10) и после этого поочередно умножим на _cos ^πz

2 H

¹ R ⁴( z )ln R ( z ) - ³ R ⁴( z ) + ¹ R ²( z ) R 2 - ¹ R ⁴ | f ^,2( z ) +

2            R ,     8          2             8 ¹ J

H

П = 2 nG J

+1 2 R ³ ( z ) tga In Rz ) - R ³ ( z ) tga + R ,² R ( z ) tga | f ’( z ) f '( z ) + V                ^R i                            J

+ | R ²( z ) + 7 R ²( z )ln RS- + 2 R4z ) tg2a In Rz ) + V 8          R                  R

dz

и sin πz и полученное выражение проинтегрируем 2H по z от нуля до H . Тогда получим алгебраические уравнения относительно постоянных c1 и c2 . Ре-

шая это уравнение, для c ₁ и c ₂ получим

₊ 9_ R ⁴( z )

32 R ₁ ²

- 32 R 2 | f ' ² ( z )

-

2 nG ( R ₀ ² - R ,² ) ^{f (} z⁾

где G – модуль упругости сдвига материала уплотнителя.

Из функционала (9) на основе уравнения Эйлера [7,12] будем иметь

Г R ⁴ ( z ) In Rz ) - 3 R ⁴ ( z ) + R ² ( z ) R ,² - 1 R ,⁴ ^ "  ( z ) +

c ₁

A 1

B₂ — ^П B₃

B, — ^^T-A 2 — П 2 A 3

2 8 HR ,	B 3 V	B 2
R 22 — R ,2
		A 2
		r
— H ( R 02 П v	- R )	1
V		V

—

—

—

B 2

π _{A 3}

— ^П Въ

—

A , • c !

A 3

—

J

π _B

A 2 — П A 3 2 J

I

• q

,

J

c 2

A 2

—

^П A <^Jv2 2 ³

Г 28HR ,

R ² — R ,

—

--^{( R} 0 ^— R , ) • q I ’ n             J

+ I 4 R ³ ( z ) tga In^( - ) - 2 R ³ ( z ) tga + 2 R ( z ) R² tga 1 ^ '( z ) +

V                   R ,                               ' J

+ 2 R2 (z) tg 2 a In R(z) — R2 (z) tg 2 a + R2 tg 2 a R1                       1 — 7 R 2( z )ln R(z) — 2 Rl(z) + 41R2 v 4           R,    ,6 R,2     ,6 * — 2R 2 (z ) J ^(z)+ + 2 q (R О — R,2 )= 0, (10) где ^(z) = f' (z) , q =---- 6---- . 4 nG (R o2 — R 2) Граничными условиями будут MQ\z=H = 2nG JYzrrdr ’ R1 (11) w\z =0= 0 ’ (12) u (r, z) z=0 = —8 , 1 r=R, (13) где

H

A 2 = J

H

A = J

/

—

π ³          π z

----g , ( z ) sin — +

16 H ^{3 1} H

n . . . nz

+--- g ₃ ( z )sin —

/

—

π ²           π z

---7 g ₂ ( z )cos --- + 4 H ^{2 2}       2 H

π         πz g (z)cos2

8 H ^{3 1}        2 H

П z x 2 П z +--- g ( z )cos --- I 2 H ³       2 H

—

1 ^H         πz

A = — [ g ₂ ( z ) cos--- dz ,

3 H ₀ 3       2 H

I

dz ,

J

^П — / x • ^П z , ---  g , ( z )sin--- +

8 H ^{2 2} H

dz ,

J

где µ – коэффициент трения между шайбой и торцом уплотнителя.

Полученное уравнение (10) является дифференциальным уравнением с переменными коэффициентами. Его решения осуществимы приближенным методом Ритца. Для этого решение дифференциального уравнения (10), удовлетворяющего граничные условия (12), выберем в виде

H

S , = J

B

n / x • 2 nz --  g. ( z )sin ---- +

8 H ³ *       2 H

П         2 П z

+--- g ₃ ( z )sin ---

I 2 H ³       2 H

/

H

-2= J

—

π3         πz g (z) sin 16H3 1 H

n . . . nz

+--- g ₃ ( z ) sin —

—

П ²      , X . nz , ¹

---  g, ( z )sin--- +

8 H ^{2 2} H

dz ,

J n2 z x ■ 2 nz I ---7 g2 (z)sin ---+

4 H ^{2 2}       2 H

dz ,

J

1 H         π

B. = — I" g. ( z )sin ^-^dz, 3 H ₀ 3       2 H

где

a =

4 HR ₁ λ ₂

gi(z) = R4(z)ln RR^- 3 R4(z) + R2(z)R2 -iR, g, (z) = 4R3 (z)tga In^z) - 2R3 (z)tga + 2R(z)R2tga ,

• 2                            _{R 1}                                 1

g з ( z ) = 2 R ² ( z ) tg² a In Rz ) - R ² ( z ) tg² a + R²tg² a -

R ₁

.

• - 2 R 2 ( z ) - 7 R 2 ( z )ln R ( z ) - — R l^ + 41 R 2

4          R1    16 R1216

Радиальное напряжение в любой точке уплотнителя может быть определено по формуле

Or = G (28 + S),(18)

где s – функция гидростатического давления [1].

Найдем s из граничного условия

О * m = 0,(19)

rr = R , ( z )

где ^R i^{( z} ) = ^R i ⁺ u i⁽ r , ^z V_R .

r <1

Тогда из условия (19) с учетом выражений (6) и (18) получаем s J R^z) +1)f'(z).               (20)

V R i² ( z ) J

Осевая нагрузка Q для поджатия уплотнителя до первого соприкосновения его внутренней поверхности со стенкой цилиндра может быть определена по формуле

ПR02 - Ri2 0z|z=H = Q .(21)

С другой стороны o = G (28 z + s ).(22)

Из выражения (21) с учетом выражений (14), (15), (16), (17), (20) и (22) получим q = f R, . +3 'I f ‘( h ),

V r i2 ( h )

где q = —r Q .

nG ( R 0 - R i² )

С другой стороны, из граничного условия (11) будем иметь

2 R 0 - R о R i - R³           2 R о tga            ,₂₄₎

q =               f ^{( H} ) ⁺ f ^{( H} ) . ⁽⁾

6 ^ ^{( R} 0 ^{+ R} i )            M\^R 0 ^{+ R} i )

Приравнивая выражения (23) и (24), определим q в явном виде

^ 2 2 ( a 5 ^-( ⁱ + a 4 ) a 2 )

π

—

-

πλ

¹ aa

2 H ²⁴

-

-

— a ₃ + a,

+

+

n | 2 2 ( a 5 - ( i + a ₄ ) a ₂ )

n2 ( a ₃

—

a _i a ₄ )

-

-

πλ

—^L ( aa

2 H ^{2 4}

-

—

2 H I 2 2 ( a 5 - ( i + a 4

) a 2 ) ^- |H ( a 2 a 4

—

a ₅

-

^{2 2} i ⁽ a 2 a 4

-

a ₅

a ₁

-

π

— a 3 + a₍

+ R i

2 з I 2 2 ( a 5 - ( i + a 4

) a 2 ) ^- Пн ( a 2 a 4

-

a ₅

b =

X

—

a 5 — ( i + a 4 ) a 2

πλ ² ₃ 2 H

i2 2 2 1 ^П ( i + a ₄ ) a _i

—

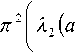
( i + a ₄ ) a ₂ ) - ^П *²- ( a ₂ a ₄

2 2 ( a ₃

—

a i a ⁴ ) ( H ( П 2 ^{( i +} a 4 ) a i

—

π

— a , + a,

2 3     6

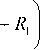
² 2 ^{( a} 5   ^{( i + a} 4 ) a 2 ) 2 H ⁽ a 2 a 4

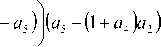
π a^

-

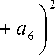
a ₅

) )

-

π

^- — ^a 3 ^{+ a} 6

+

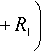
² 3 I ² 2 ^{( a} 5   ^{( i + a} 4 ) ^a 2 ) .„( ^a 2 ^a 4

V                 2 H

+

—

__________________ R i² 2 2 - R 0² _________________

^7П_н13Г V ² 2 ⁽ a 5 ^{-( i +} a 4 ) a 2 ^)— nH ⁽ a 2 a 4 ^- a 5 )

I П           П i6H Ri221 —(i + a4)ai - — a3 + a6

-

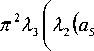
( i + a 4 ) a 2 ) - ^{П 1}- ( a 2 a

(

-

a ₅

)

) ⁾

π

) a i — —a 3 + a 6

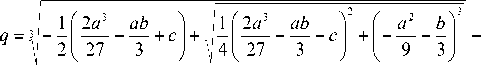
a

^c = 7----/-----\—72 x

( a 5 ^- ( ^{i +} a 4 ) a 2 )

^П 2-1 2 ( a ₅ - ( i + a ₄) a ₂) - ^П ^( a₂a₄

V 8 H ² V                 2 H ^{2 4}

—

+

I ^{п            n}

^{2 R} i ² 2 I у ^{( i +} a 4 ) a i - "2 a 3 ⁺ a 6

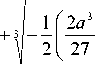
ab )   / i I 2 a³ ab ) 2 ( a ² b I

3 ⁺ c J 44 V 27   3 ⁺ c J +V 9 ⁺ 3 J

—

⁺ „ 3₃ /---------------------- Ta------------

—— | ² 2 ^{( a} 5 ^{- ( i + a} 4 ) a 2 ^{) —     (} a 2 a 4 - a 5

8 H V                2 H

+

8 Л 2 I — ( 1 + a ₄ ) a 1

—

π

2 ^a з + a 6

+

^П I к ⁽ a 5 ^{—( 1 +} a 4 ) a 2 ^)— 2 H ⁽ a 2 a 4

—

—

—

Х 1 ( a 3

—

, n i

I a i —    a з + a 6 I + R

,

Z^ ( 7 ⁽ a 5 ^{—( 1 +} a 4 a 2 ) 2 H к

—

πλ

^{( a} 2 ^a 4 ^—

2 H

a 1 =

B 1

—

B₂ — ⁿ в

π

AA

₃     R 2²

A 1

2 δHR ₁

—

R 1²

B 3

B 2

—

—

π_B 2 ³

A

к

^A 2 ^—

π_A 2 ³

A 3

,

a2

H ( R 0 — R ) π

/

a3

B 2

Bi —

A 2

A 3

—

—

π _B

2 ³ A 1 π _A 2 ³

к

B 2

—

A 2

a 5 =

A 2 — П A 3 R 2

2 δHR ₁

—

^R 1²

,

H ( R 0 — R 1 ) π

,

a

A 2

—

π_A 2 ³

Из выражения (25)

— ⁿ Bi

—

,

^П А з- 2   7

a ₄ = —

A 2

A 1

—

π _A 2

—

⁶      R 2 ²

2 δHR ₁

—

^R 1 ²

.

,

определяется величина

осевой нагрузки, необходимой для поджатия уплотнительного элемента до первого соприкосновения его наружной поверхности со стенкой цилиндра.

Второй этап. Теперь определим величину осевой нагрузки, необходимой для полного соприкосновения наружной поверхности уплотнительного элемента со стенкой цилиндра. Начало координатной системы также поместим в центре нижнего сечения уплотнительного элемента, ось z направим вертикально вверх, a ось r – в сторону увеличения радиуса, как показано на рис. 2. Принимая гипотезу плоских сечений и, соответственно, предполагая, что осевая деформация уплотнительного элемента зависит только от координаты z в осевом направлении_, можно также принять

w 1 = f 1 ⁽ z ) .

где w₁ – осевая деформация сечений уплотни-

тельного элемента, f₁ (z) – неизвестная функция,

зависящая только от z .

Тогда из условия несжимаемости (2) с учетом формулы (26) получаем

u1

1 г 7 з ^C 4 ^— - rf 1 ⁽ z ) ⁺ — .

2 r

где c ₄ – постоянная интегрирования.

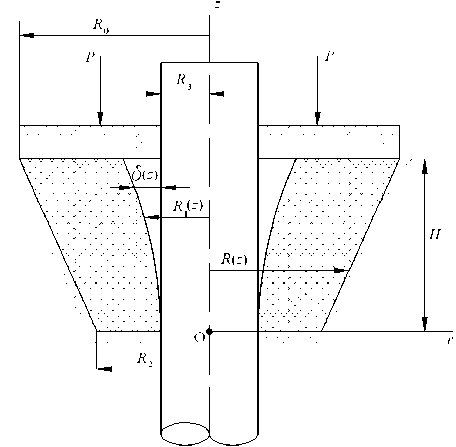
Рис. 2. Расчетная схема.

Граничное условие u\ =0 . 0 ■                     (28)

• ¹    l r = R ( z )

Тогда из выражения (27) с учетом граничного условия получаем

1 f R ² ( z )     A ' \                   f7Q1

Ui ,             r I f . ( z ) ■                   ⁽²⁹⁾

• ²    к ^r 7

Для потенциальной энергии уплотнительного элемента после его деформации с учетом осесим-метричности будем иметь h R(z)                              i                           h , n = 4nGI I I er2 + s^g + £^2 + -/2z I rdrdz — |P• f1(z)dz

0 R ₃ ^{к                    2 7}             0

(30) где P – осевая нагрузка необходимая для полного соприкосновения наружной поверхности уплотнителя со стенкой цилиндра, R ( z ) = R ₂ + z • tga ,

tga = R^HR^ , h = H —^ , A = f ( H ) ■

Подставляя выражение (29) в формулу (8), а полученные результаты в выражение (30), а далее интегрируя его по r , из полученного функционала на основе уравнения Эйлера [6, 12] будем иметь

I R 4( z )ln R(z) — 3 R 4( z) + R 2( z) R2 —1R,1 к (z) + к          R3    4                 3 4 3 J

+1 4R3 (z)tga In R(z) — 2R3 (z)tga + 2R(z)R2tga Ik (z) + к              R 3                            7

+

2 R ² ( z ) tg 2 a In RRz) — R ² ( z ) tg 2 a + R 2 tg 2 a —

—

к

2 R ²( z ) — 4 R ²( z )ln R(z)

R ( z ) 9 R ⁴ ( z ) 4 1 2

-----1-- R

16 ³

+ 1 p ( R ²( h ) — R 2 ) = 0 ,

где ^ i⁽ z ) = f i ⁽ z ) ■

16 R ² ₃

^ i^{( z} ) ⁺

Граничными условиями будут

R(h) gP\z = h = 2nG J Yzrrdr , (32) 3 u 1 lr=R1(z) = —§ (z) , (33) ^- z=0 = 0 , (34) где R(z) = R + u (r, z)| r=R , §(z) = § + u (r, z)| r=R .

где h 3                            2

.i     fl ⁿ i , . . ⁿ i , .       2 Л2      ⁿ i , , . Ж I ,

A, = I-- 7 g ,( z )sin +-- 7 g A z )cos —+-- g A z )sin— I dz

¹ J к 16 h³          h   4 h²           2 h 4 hh J

h

^A 2 = J

n     1, .      2 nz    n     1 , . . nz

--7- g ,( z )cos--- gg ₂( z )sin — +

8 h ^{3   1}            2 h   8 h ^{2   2} h

dz ,

Полученное уравнение (31) является дифференциальным уравненем с переменными коэффициентами. Поэтому решение его осуществима приближенно методом Ритца. Для этого решение дифференциального уравнения (31), удовлетворяющего граничные условия (34), выберем в виде

I        n I п c f, (z) = C, 1 - cos  + C, sin+ — z,     (35)

^{J 5} к         2 h J 6     2 h h

, П 1 , .      2 nz

+ g з( z )cos — к 2 h           2 h

h

A¹ = — [ g i ( z )cos — dz , ³ h ^J ₀^S3V '     2 h

h

^{B 1} = J

J

где c ₅ , c ₆ и c ₇ постоянные, подлежащие определению.

Постоянное c ₇ вычисляется из граничного условия (33)

^C 7

—

2 h δ ( z ) R ₁ ( z )

R ²( z ) — R i ²( z )

—

π   πz c sin

5 2    2 h

—

c ^π cos ^{π z} . (36)

6 2    2 h

Подставим выражение (35) в уравнение (31) и после этого поочередно умножим на cos ^{π z} и 2 h

sin π z , полученное выражение проинтегрируем по 2h z от нуля до h . Тогда получим алгебраические уравнения относительно постоянных c5 и c6 . Ре-

шая эти уравнения для c ₅ и c ₆ , получим

A

A

—

—

π   πz

A ₃ ¹ cos

к

—

B

—

—

i

i

c ₅

к

к

A

к

^c 6 =

A

B

—

π

—

к

B

—

2 h _B 1

1 π    πz

B ₃ ¹ cos

—

2 hδ ( z ) R ₁ ( z )

R ² ( z ) — R । z )

—

2 h

πz

J

π   πz

A ₃ ¹ cos

—

B 1

B

₁ π π

B ₃ ¹ cos

—

I

|h h ( R ² ( h ) — R3>P nz n

2 h J

1 π   πz

B ₃¹    sin

I

I

J

—

sin

к

2 h _{A 2}1 B ₃ ¹ π cos π^z

πz

2 h

π   π z

B ₃ ¹ cos

2 h

—

—

B 1

—

B

2 h

J

πz

π   πz

B ₃¹    sin

I

—

2 h

π   πz

B ₃ ¹ cos

2 h

cos

πz

2 h

A

J

J

( 2 h 8 ( z ) R i ( z )

X

R ² ( z ) — R 2 ( z )

—

к

B ₃

—

B 1

—

nl ⁿ • ⁿ I B 3 — sin— p c

2 h

—

h ( R ²( h ) — R з² ) • p π

J

П 1 . . . 2 nz П 1 . . . nz --Г g 1( z )sin --- + Г g ₂( z )sin--- + 8 h³¹       2 h  8 h²²      h

^{П         n z}

+ g з( z )sin --- к 2 h ³        2 h

dz ,

h

^B 2 = J

—

π        πz g1(z)sin

16 h ^{3 1} h

П 1/ ₄ - nz +77 g з^{( z )si}n-r-к 4 h         h

J

π        πz

--n g ?( z )sin --- +

4 h ^{2 2}        2 h

dz ,

J

B 3 =1J g 3(z )sin nhdz, g 1 (z) = R4 (z) In RR(z) — 3 R4 (z) + R2 (z)R32 — 4 R34, g 1(z) = 4R3(z)tga In R(z) — 2R 3(z)tga + 2R(z)R32tga ,

^{2                          R} 3                               ³

g 3 ( z ) = 2 R ² ( z ) tg 2 a In R ^ z ) — R ² ( z ) tg ² a + R 3² tg ² a — R ₃

— 2 R ²( z ) — 7 R ²( z )ln R I z ) — 2 R !( z ) + 41 R ₃2

4           R ₃    16 R ₃ ²     16 ³

.

Осeвое усилие, необходимое для деформации уплотнительного элемента до полного соприкосновения его наружной поверхности со стенкой цилиндра, может быть определено по формуле

^{n ( R 2( h} ) ^{— R} 3² )^ z| z = _h = ^P ,

где σ _z – осeвое напряжение в любом поперечном сечении уплотнительного элемента.

После полного соприкосновения наружной поверхности уплотнительного элемента со стенкой цилиндра граничное условие на верхнем сечении его будет

CT r = R 3 = 0 . ^r z = h

Тогда из выражения (18) с учетом граничного условия (40) получим

s =

I R^h к R 3

+ 1 | f 1 ' ( h ) .

Из выражения (39) с учетом выражений (22) и (41) получим

/

P =

к

R 2     ।

-T + 3 / 2 ( ^h ) , _ R 0 J

‘

где p = —i—P ----1.

nG ( R ²( h ) — R ₃ ² )

С другой стороны, из граничного условия (32) будем иметь p = 1R (h) — RоR3 — -R3 f "(h) + 1R(h)tga f'(h) . (43)

^P     6 ^ ( R ( h ) + R ₃ ) ^{J1 ( }} A( - ( h ) + - ₃ ) ⁷¹ °

Тогда из выражения (42) и (43) с учетом формулы (35) и выражений c ₅ , c ₆ и c ₇ получим

ν ₂

—

—

π ²

(

p =— ^v

ν ₀

V

5 ( h ) R ( h )        5 '( h ) R ( h ) + 5 ( h ) R ( h )

+                     +

¹ R ²( h ) — R 1² ( h )     ²       R ²( h ) — R 1² ( h )

^{+ V} 3

‘

5 ( h ) R 1 ( h )    R ( h ) tga — R 1 ( h ) R 1 ( h )

R ² ( h ) — R 12 ( h )

R ² ( h ) — R 12 ( h )

— 2 hv 4

5 "( h ) R i ( h ) + 2 5(h ) R 1 ( h ) + 5 ( h ) - 1 ( h )

R ² ( h ) — R 1² ( h )

+

"

+ 4 _{h v}     5 ( h ) R 1 ( h )    tg ²a — R 1² ( h ) — R 1 ( h ) R 1 ( h ) +

⁴ R ²( h ) — R 1² ( h )          R ²( h ) — R 1² ( h )

‘

+ 8 h v ₄

5’(h ) R 1 (z ) + 5 ( h ) R 1 ( h ) R ( h ) tg a — R 1 ( h ) R 1 ( h )

R ² ( h ) — R 1² ( h )

R ² ( h ) — R 1² ( h )

—

-1т ^ 6 1 2 h $ 2

B 2    V

—

_ 2 B 3 e ¹

n 5 i I —

B 2   J

A^f B 1 — B 1 ^п I A ² 5 — 2 h |

В 1³ I ^{1       3} 2 J ^{6 3} I

B ₂

,

I                         1

v₃ = 27- a I 2 h5 — n² B 3 5 J + 1 n ²-Y I B ; — B 1 ⁿ I a 5 +

3            1    6          2               1    3                    13       1        3          63

B 2 V          B 2 J      B 2 V

- f     R1 1 R1 f

+ 8 A — 2 n ²| 1 — B ³ J B ³ A + 4 h | 1

⁴ V    B 1 J B 1 ⁴ V

V 4 = -11 A 6 5 3 + A 4 1 1 —

B 2           V

A =

2 R ( h ) tgα

A 6 =

I A 1

^ ( R ( h ) + R 3 )

^A 3^{1 B} 2¹

^A 7 = 7

I A 1

—

B 3 U -

I A ,

B 2 J ⁵

—

—

π _A 1 2 ³

—

B

B

J , _A = 2 R ²( h ) — R 0 R 3 — R 3²

1 2 J    ⁴       6 ^ ( R ( h ) + R ₃ )

R ² ( h )

—

^R 3²

^A 2^{1 B} 3¹

— 3 ,

B 1 — B 1 ^п I A ^{1     3} 2 J B.

A 2 — B 1

π _A 1 2 ³

^B 1^{1 —}

,

^, 2¹ 1

,

D1 ^{П 1} A 2

B I

³ 2 J B 2

_{- 1},.      5 ( h ) R ( h ) V R ( h ) t ₈ ^{a -} R 1( h ) R 1 ‘( ^h )У '

^V4 R ² ( h ) — R 1² ( h )      ( r ² ( h ) — R 1² ( h ) ) 2

,

A = 7------

I A 1 — ⁿ A 1

V ¹     2 ³

^{A 31 B 31}

_{B 1} 1 _—

,

D1 ^{П 1} A 2

B l I 1

³ 2 J B 2

J

где v о = 4r (R 02 — R 32 )x

B 2¹

5 1 = J ²

4 h

f                    ¹

ⁿ 1 1 — B ³-1 A +

2 h V    B 2 J 4

+±

B 1

v ²

—

A

J

X

π

~ -rl 5

4 B 1¹

—

V

^П B 5 II B 1 h B Г³ JV ¹

—

π _B 1 2 ³

—

n, Y

7 ⁵ 3 ^A 6 ⁺

4 _J

5 =_— ⁿ L ^f1 ²      2 h B 1 V

B

—

B

' 3 I ^f D1 D^{1 П 1} , Й" JI B 1 ^— B 3 A J ^A 4 ⁺ ' 2 JV ² J

+ 5 1 he 2 π

—

ⁿ 2 e I 1 , ⁿ Is

1 ^A 8 ⁵ 3 I ^X 7 ⁺ л I ⁵ 2

16 h J 4 V

—

n ² B L 1

Г 5 з Аб +

2 hB 2 J ⁶

11. n

+ 1

VV 2

—

^B 2¹

B 1 — B 1 ⁿ || A

^{1       3} 2 J J ⁵

+ ^{П f П} A + A J B 1

4 I 2 h ^{4     5} J ³

—

П ^{f 1} X 4 + X 5 J B 2 4 V h J

3           12

_— —X B3- _— 8 h ⁴ B ₂ ¹

I A ,

—

π ² 1 16 h B ₂ ¹²

,

, 1 f R ²( h )   _D

5 ( h ) = 5 + -| —— — R

2 V - 1        ¹

π    πhc c,---sin---+ c,---cos+ —

1 2H   2H

π

2 H H

² «1 f

V, = —г A l 2 h5 3 1 4 h5

¹ B\ ⁶ 1       ¹ 8/i B\ (      ²

—

B ¹    11   ,r⁴

П 5 J l+ ?AA5

B 2 ³ JJ 16 hB 1^{2 6}^ ³

R ( h ) = R , +^{1 f} R -( h ) — R, 1 2 V R 1        1

πhc c,---sin---+ c,---cos+ —

1 2H   2H

π

πh

π

—

2 H

2 H H

π 2 1

8 h B ₂ ¹³

R 1

4 5 — n -1 5 3 B 1

B 2 J ^V

— ⁿ B 1 | a^ 2 ³ J ⁶

2 π ³ 1      2

⁺i h B^{2 л} ‘ ⁵ 3 ^—

R ' ( h ) = 1 1 R 7( h )

2 V R 1

—

R 1

π ²

πh

c cos

¹ 4 H ²    2 H

—

n ² . nh | c,---- -sin---- +

² 4 H ²    2 H J

.

—

П 4 1 f B - 8 h B 2⁵ V ¹

—

2      41

ⁿ B 1 1 A³ 5 + 3 ⁿ —т I B 1

2    3     6 3      8 h ₁ 4     1

B ₂

^— B 3 A ] ^A 6^{2 5} 3 ⁺

B ₃

■

B

-1 f

π ²

2 h

V

^f 1 — — B^{1 f} 1 — B^ J J a + ^f — ^f 1 — B ¹ )- 2 ) A 1 , V 2 B 2 V B 2 J ^{J 4} V 2 V B 1 J ^{J 5} J

R ( h ) tga I n . nh      n     nh c, 1

+--- c.--- sin--- + c, cos--- + —

R 1 V 1 2 H 2 H 2 2. H   2 H H J

Контактное давление между наружной поверхностью уплотнительного элемента и стенкой цилиндра после полного их соприкосновения можно определить по аналогии балки на упругом основании

^ r ⁽ z ) = k 0 • u 0⁽ z ) ,

где k ₀ – коэффициент постели.

u 0 ^{( z} ) = ^R 1 - R 3 + u ⁽ r , z ^ _R ■ ⁽⁴⁶⁾ Г R

Если при этом не обеспечивается герметичность стенки, тогда продолжают сжимать уплотнительный элемент. Тогда на расстоянии z от нижнего основания уплотнителя выделим кольцевой элемент высотой dz и составим для него уравнение равновесия n (R2(z) - R32 )| a, - a —d: | + T • 2nR dz +

3 zz3

x            V          5z    )

+ T 1 • 2 nR ( z ) - dz - + N sin a • 2 nR ( z ) - dz- — 0

cosαcos

Обсуждение результатов

Результаты численных расчетов представлены на рисунках 3, 4, 5. Как видно из рис. 3, величина осевой нагрузки, необходимая для первого соприкосновения наружной поверхности уплотнителя со стенкой цилиндра с увеличением высоты уплотнителя, сначала растет, а потом стабилизируется и в некотором значении высоты перестает расти. Осевая нагрузка, необходимая для полного соприкосновения наружной поверхности уплотнителя со стенкой цилиндра, с увеличением высоты уплотнительного элемента также растет (см. рис. 4).

где τ , τ ₁ – касательные напряжения, c другой стороны, с учетом несжимаемости материала уплотнителя закона теории скольжения получим [7]

t — ц • a r ; N — a r cos a ; T 1 — ц • N ; ^ — ^V~ a ’ r 1 - v ^z

(48) где µ – коэффициент трения, ν – коэффициент Пуассона.

Подставляя выражение (48) в уравнение (47) и проинтегрировав полученные выражения с учетом граничного условия a — a , получаем ^z z — h      ⁰

2µν a — a0 •(R (z) - R3 Г * '" (R 2( z) - R3 )1-v cos“,     (49)

где σ0 – осевое напряжение в сечении уплотни- тельного элемента, где приложена сила сжатия.

Распределение контактного давления между внутренней поверхностью уплотнителя и стенкой цилиндра может быть определено из выражений (45) и (49) следующим образом a — a-              (50)

r 1 - v z тогда из выражения (50) с учетом формул (45) и (49) получим

2 µν

(1-v *tga                         V cos a ar(z) — у-vсто •(R(z)- Rз)      (R^(z) - R32)1-v     +

⁺ k 0 • u 0 ( ^z )

Величина σ ₀ может быть определена из условия герметичности

2 µν

Va 0 •(R(z) -R 3 *( *g (R2(z) -R 32 ^C0Sa + k 0 • u 0 (z *^ P * 1 - v где P* - давление среды.

Произведен численный расчет по формулам (25), (44) и (51) значений осевой нагрузки, необходимой для первого и полного соприкосновения наружной поверхности уплотнительного элемента со стенкой цилиндра, а также характера распределе-

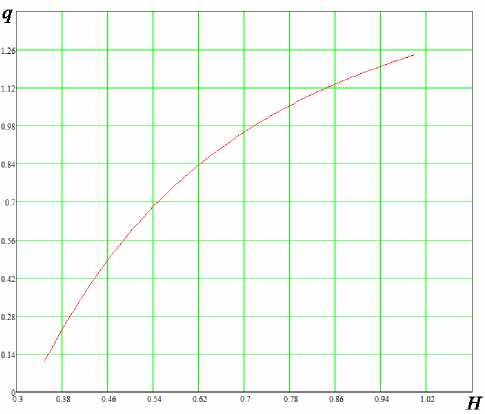
Рис. 3. График зависимости осевой нагрузки, необходимой до первого соприкосновения внутренней поверхности уплотнителя сo стенкой цилиндра от его высоты.

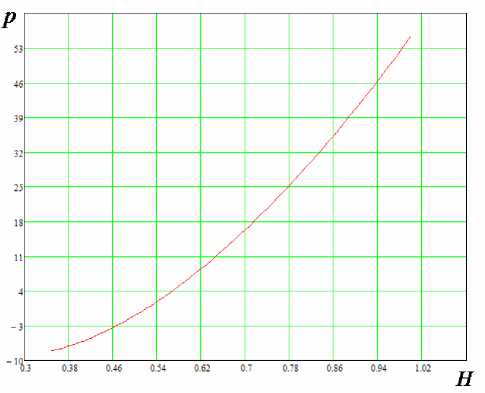
Рис. 4. График зависимости осевой нагрузки, необходимой до полного соприкосновения внутренней поверхности уплотнителя сo стенкой цилиндра от его высоты.

ния контактного напряжения σ _r при следующих значениях параметров: R 0 — 0.118 м , R 1 — 0.04 м , R ₂ — 0.1 м , R ₃ — 0.037 м , 3 — 0.003 м , P *— 2•Ю ⁷ Па , G — 1.3 • 10 ⁸ Па , к ₀ — 6.7 •Ю⁷ Па / м , ц — 0.5 , v — 0.25 .

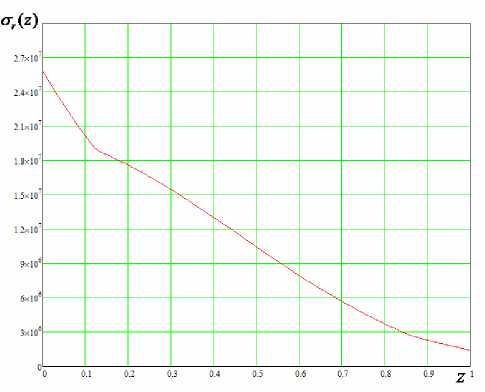
Рис. 5. График зависимости характера распределения контактного давления между наружной поверхностью стенки цилиндра и внутренней поверхностью уплотнительного элемента в зависимости от координаты z .

Из рис. 5 видно, что контактное напряжение между наружной поверхностью уплотнительного элемента усеченной конической формы максимальное значение принимает в его нижнем сечении и с ростом координаты z оно уменьшается и в верхнем сечении, где приложена осевая нагрузка, принимает наименьшее значение.

Заключение

Получено аналитическое выражение (51), позволяющее определить характер распределения контактного давления между внутренней поверхностью уплотнителя и стенкой цилиндра в зависимости от его физико-механических свойств и геометрических размеров с учетом краевых эффектов.