Математическое моделирование и методы детерминации обрыва стержней ротора асинхронного двигателя

Асинхронные электродвигатели с короткозамкнутым ротором благодаря простоте своей конструкции и обслуживанию получили наиболее широкое распространение в качестве электроприводов технологического оборудования металлургической и энергетической отраслей. В процессе эксплуатации асинхронные электродвигатели испытывают значительные нагрузки из-за частых или тяжелых пусков, что снижает уровень их надежности и в дальнейшем может привести к их полному выходу из строя. Как показывает статистика [1, 2], 17 % выхода из строя асинхронных электродвигателей связано с повреждениями обмотки короткозамкнутого ротора, среди которых обрыв стержней достигает порядка 80 % от всех отказов. Своевременная детерминация оборванных стержней короткозамкнутого ротора в самом начале развития повреждения позволяет предотвратить полный выход из строя асинхронного электродвигателя, поскольку длительная работа с оборванными стержнями может привести к задеванию ими обмоток и магнитопровода статора.

Постановка задачи

Используемые на сегодняшний день методы диагностирования обрыва стержней короткозамкнутой обмотки ротора асинхронного электродвигателя в своем большинстве основаны на спектральном анализе токов статора [3–7]. Однако такой подход обладает сложностью оценки полученных результатов, так как в полученном спектре учитываются любые возникающие модуляции, что приводит к снижению точности выявления наличия оборванных стержней короткозамкнутой обмотки ротора. Таким образом, актуальной является цель работы, которая заключается в разработке методов детерминации обрыва стержней короткозамкнутой обмотки ротора по параметрам рабочего режима с использованием математической модели для проверки их эффективности.

Математическое моделирование обрыва стрежней ротора асинхронного электродвигателя

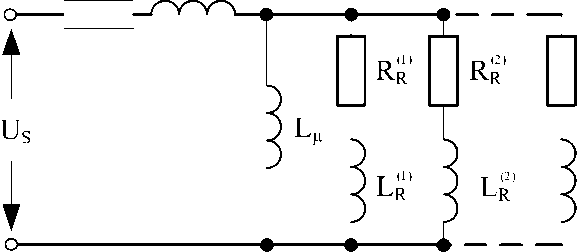
Для составления математической модели примем за основу эквивалентную многоконтурную схему замещения асинхронного электродвигателя, приведенную на рис. 1.

В приведенной эквивалентной многоконтурной схеме замещения (см. рис. 1) каждый стержень короткозамкнутой обмотки ротора описывается отдельной ветвью, содержащей активное сопротивление ( R_R ^{(i )} ) и индуктивность ( L_R ^{( i )} ). Количество таких контуров в математической модели асинхронного электродвигателя будет зависеть от числа стержней ротора ( i ). В отличие от существующих математических моделей [2, 8] в предлагаемой выполнен учёт сопротивлений участков колец, соединяющих между собой стержни короткозамкнутого ротора в его лобовых частях. Помимо активного сопротивления и индуктивностей стержней ротора схема замещения содержит также активное сопротивление ( R_S ) и индуктивность ( L_S ) обмоток статора и индуктивность ветви намагничивания ( L _μ). Для определения параметров математической модели в соответствии с приведенной схемой замещения может быть использована методика, приведенная в [9].

Поскольку существующие методы диагностики обрыва стержней короткозамкнутой обмотки ротора основываются на измерении фазных токов, то математическую модель целесообразно представить в трехфазной системе координат для токов статора. При таком подходе должен быть выполнен учёт зависимости потокосцеплений и индуктивностей электродвигателя от угла положения ротора, поскольку токи ротора остаются представленными в двухфазной системе координат. Таким образом, математическая модель асинхронного электродвигателя, записанная с помощью системы дифференциальных уравнений, в матричном виде будет иметь вид:

R S      L S

_{R R} ( i )

( i ) L R

Рис. 1. Эквивалентная многоконтурная схема замещения асинхронного электродвигателя

Fig. 1. Equivalent multi-loop circuit of an induction motor

d * s dt d * r dt

U S

UR

R S

R R

— = — Г M_B - M _c (с о ) П ; dt   Tj^L вр      ^{c J}

d y

— = ю , dt

■ L ( Y , Ф ) - ¹

* S

T

;

где L ( y , Ф ) - матрица индуктивностей статора и

ротора;

U_S = [ u A , u B , u C ] Т и U_R = 0 - векторы напряжений обмоток статора и ротора;

• * S = [ v A , V B , V C ] T — вектор потокосцепле-ний статора;

(1)     (2)         ( i )     (1)     (2)         ( i ) ^T

^T R = [ ^V R a , ^V R a ’—’ ^V R a , ^V R p , ^V R p ’—’ ^V R p J вектор потокосцеплений ротора;

• ю - скорость вращения ротора;

R_s = diag [ R_s , R_s , R_s ]

и

R r = diag [ R a ¹ ) , R a ²⁾,..., R «, R® R < ²⁾,..., R «J -диагональные матрицы сопротивлений обмоток статора и ротора;

M _вр – электромагнитный вращающий момент

где K _СР – коэффициент, учитывающий количество стержней ротора.

Алгоритм формирования подматриц индуктивностей в зависимости от количества стержней и угла положения ротора подробно описан в [10].

Моделирование обрыва стержней короткозамкнутой обмотки ротора асинхронного двигателя выполняется путем изменения величины активного сопротивления и индуктивности заданного стержня. Предложенная в работе математическая модель асинхронного электродвигателя позволяет задать любое количество оборванных стержней короткозамкнутой обмотки ротора путем указания их порядкового номера, при этом происходит автоматическое перестроение матриц активных сопротивлений и индуктивностей.

на валу двигателя;

M _c - момент сопротивления; y - угол положения ротора.

Для определения величины электромагнитного вращающего момента на валу двигателя на основе токов и потокосцеплений статора может быть использована формула

^M вр = ^ [ ( i B — i C ^ V A — ⁽ V B — V C ) i A J •

Момент сопротивления на валу асинхронного электродвигателя может определяться по следующей формуле:

Mc = Kзагр ■ю2, где Kзагр – коэффициент загрузки асинхронного электродвигателя.

Поскольку математическая модель предназначена для моделирования любого количества стержней в короткозамкнутой обмотке ротора, то в этом случае при формировании матрицы индуктивностей двигателя необходимо учитывать взаимное расположение стержней ротора относительно друг друга. Данный учёт выполняется за счёт определения величины угла между стержнями, которая в зависимости от количества стержней определяется по формуле

.    2 ■п

^Ф = F,

^K СР

Разработка и моделирование способов диагностирования обрыва стержней короткозамкнутой обмотки ротора асинхронного двигателя

Для разработки метода детерминации обрыва стержней короткозамкнутой обмотки ротора асинхронного электродвигателя воспользуемся преобразованием Фурье, с помощью которого любой периодический сигнал может быть представлен в следующем виде:

a   c f (t) =--+ ^a cos(nюt) + b sin(nюt),

2    n = 1 ⁿ            "

где a ₀, a n , b n - коэффициенты Фурье для n -й гар-

моники измеряемого сигнала на интервале измерений T , которые определяются по формулам:

2 t               z        , an =       f(t)cos( n ю t) dt;

t — T

,      2 t bn =       f(t)sin( n ю t)dt • t—T

Длительность интервала измерений токов статора для первой гармоники может быть рассчитана по следующей формуле:

T = f ■

где f – частота измеряемого сигнала.

С помощью коэффициентов Фурье для измеряемого сигнала можно определить его амплитуду и фазу n -й гармоники, используя следующие фор-

мулы:

X n = 7 ^a n ⁺ b n ;

Ф n

= a tan

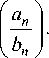
На рис. 2а приведены результаты математического моделирования работы асинхронного электродвигателя мощностью 1700 кВт, используемого в качестве привода циркуляционного насоса на электростанциях с блоками мощностью 200 МВт при исправной обмотке ротора, а на рис. 2b – при обрыве трех стержней.

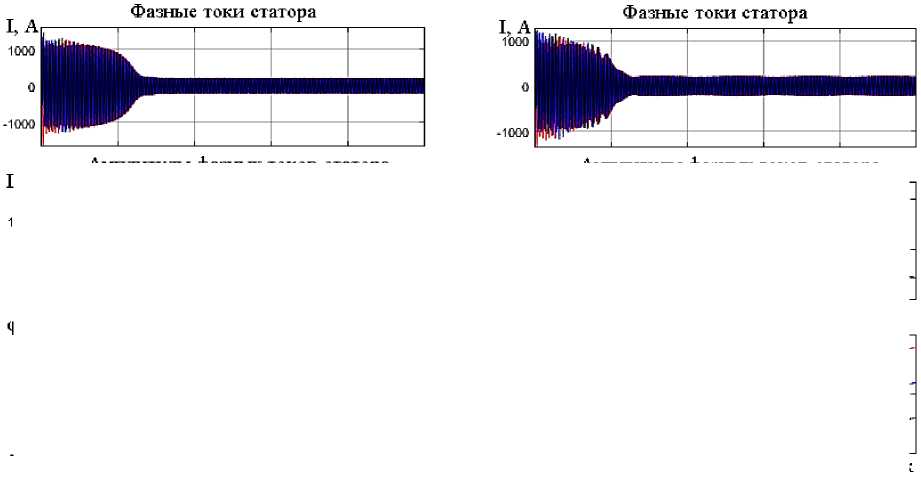
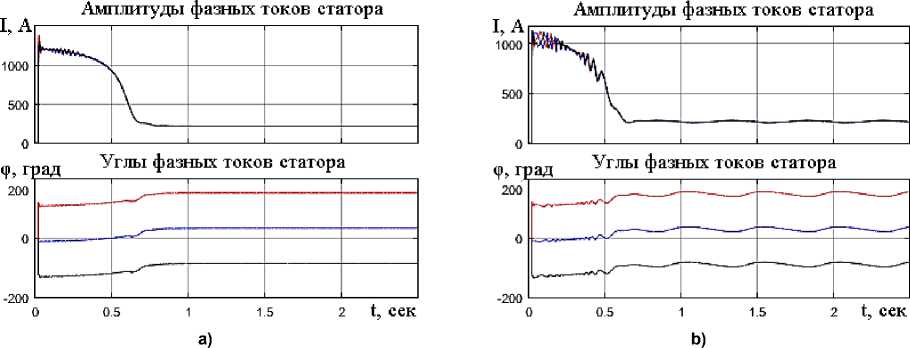
Рис. 2. Результаты моделирования работы асинхронного двигателя: а – при исправной обмотке ротора; b – при наличии одного оборванного стержня Fig. 2. Results of simulating the operation of an induction motor: a – with the rotor winding in good condition; b – with one broken bar

a)

b)

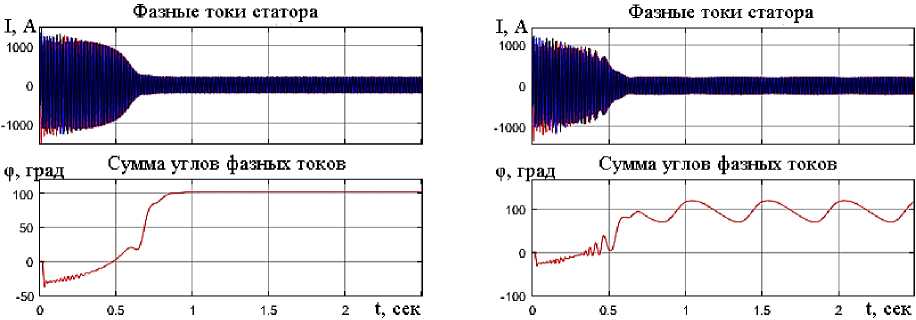
Рис. 3. Результаты моделирования предложенного диагностирующего признака по сумме углов фазных токов: а – при исправной обмотке ротора; b – при наличии одного оборванного стержня

Fig. 3. Results of modeling the proposed diagnostic feature based on the sum of phase current angles: a – with the rotor winding in good condition; b – with one broken bar

Как видно из рис. 2а и 2b, при исправной обмотке ротора величина амплитуды и угла измеряемых фазных токов остается постоянной, а в случае обрыва одного стержня в короткозамкнутой обмотке ротора происходит колебание величины амплитуд и углов измеряемых токов статора с постоянной периодичностью вследствие возникающего переменного магнитного потока, вызванного обрывом стержней короткозамкнутой обмотки ротора. Причем стоит отметить, что колебания величины углов фазных токов являются более выраженными, чем колебания амплитуды фазных токов статора.

Таким образом, полученные результаты сви- детельствуют о том, что в качестве диагностирующего признака для детерминации оборванных стержней короткозамкнутого ротора асинхронного электродвигателя может быть использовано изменение величины углов фазных токов статора с одинаковой периодичностью. Для более выраженного характера изменения величины углов токов статора возможно использование суммы углов трех фаз токов статора. На рис. 3а и 3b приведены результаты моделирования предложенного диагностирующего признака по величине суммы углов фазных токов при исправной обмотке ротора и при обрыве одного стержня короткозамкнутого ротора асинхронного электродвигателя.

a)

b)

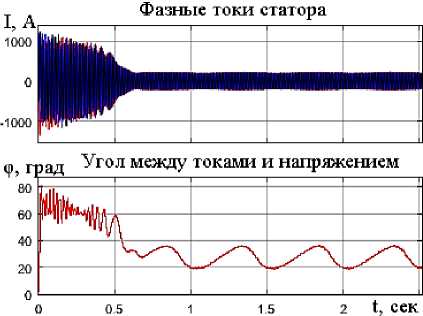
Рис. 4. Результаты моделирования предложенного диагностирующего признака по углу между фазными токами и питающим напряжением: а – при исправной обмотке; b – при одном оборванном стержне

Fig. 4. Results of modeling the proposed diagnostic feature based on the angle between phase currents and supply voltage: a – with the rotor winding in good condition; b – with one broken bar

Использование преобразования Фурье влечёт за собой необходимость тщательного подбора интервала измерений, поскольку отклонение частоты в сети от 50 Гц может привести к появлению погрешности при определении фазы и угла фазных токов статора. С целью предотвращения указанно- го недостатка при использовании предложенного метода диагностирования целесообразно преду- смотреть предварительное определение частоты измеряемых фазных токов статора для корректного выбора величины интервала измерений.

Указанного недостатка лишен предлагаемый в данной работе еще один способ диагностирования обрыва стержней ротора, который основан на измерении угла между фазными токами статора и питающим напряжением сети без использования преобразования Фурье. Определить величину угла между фазными токами и питающим напряжением по мгновенным измеряемым значениям можно по формуле

Ф = arccos

U a * i A + U b * i B + U 1 * i c

4 ⁽ u A ^{+ u} B ⁺ u C ) ■ ( i A + i B + i C)

,

где u_A, u_B, u_c - мгновенные значения питающего напряжения, i_A , i_B , i_c - мгновенные значения токов статора.

С целью отстройки от случайных помех и повышения точности измерений в работе предлагается предварительно выполнить усреднение измеряемых сигналов фазных токов статора и напряжения для центральной выборки при пяти измерениях по следующей формуле:

x ⁽ t 3 ) =     ( x ⁽ t l ) ⁺ x ⁽ t 2 ) ⁺ x ⁽ t 3 ) ⁺ x ⁽ t 4 ) ⁺ x ⁽ 1 5 ) ) ,

An где An – коэффициент усреднения; n – количество выборок измеряемого сигнала.

Поскольку функция синуса является нелинейной, а шаг дискретизации при измерении сигнала остается постоянным, то коэффициент усреднения может быть определен как отношение суммы всех выборок измеряемого сигнала к центральной выборке по следующей формуле:

A n

n - 1

^ sin ( ю* ( t₁ + h ■ n ) + ф )

r = 0

■ C C 7 n — 1 'I      , sin I ю *I t1 + h *        I + Ф| где h – шаг дискретизации измеряемого сигнала.

На рис. 4а и 4b приведены результаты моделирования предложенного диагностирующего признака обрыва стержней по углу между фазными токами статора и питающим напряжением при исправной короткозамкнутой обмотке и при одном оборванном стержне короткозамкнутого ротора соответственно.

Как видно из рис. 4а и 4b, при исправной обмотке ротора величина угла между фазными токами статора и питающим напряжением остается постоянной, а при возникновении обрыва стержней в обмотке ротора происходит изменение его величины с постоянной периодичностью из-за колебаний величин углов фазных токов статора, что может быть использовано в качестве диагностирующего признака для детерминации повреждения стержней в короткозамкнутой обмотке ротора асинхронного электродвигателя в режиме реального времени по параметрам рабочего режима.

Выводы

• 1.    Предложена математическая модель асинхронного электродвигателя, позволяющая моделировать обрыв любого количества стержней короткозамкнутой обмотки ротора асинхронного электродвигателя с целью анализа возникающих переходных процессов в обмотках статора для выявления диагностирующих критериев состояния короткозамкнутой обмотки ротора.

• 2.    Разработаны методы детерминации обрыва стержней короткозамкнутой обмотки ротора асинхронного электродвигателя безразборным способом в режиме реального времени на основе измерений фазных токов статора и питающего напряжения в рабочем режиме, без вывода асинхронного электродвигателя из эксплуатации.

• 3.    С помощью предложенной математической модели выполнено моделирование работы разработанных методов детерминации обрыва стрежней короткозамкнутой обмотки ротора асинхронного электродвигателя и подтверждена эффективность их применения.