Математическое моделирование и расчет многослойных фильтров малой толщины для сорбционной очистки поверхностного стока с загородных участков автомагистралей

В соответствии с действующим законодательством [2] дождевые и талые воды с автодорог и мостовых переходов в водоохранных зонах должны очищаться перед сбросом в водоемы. Автодорога М-18 «Кола» (от Санкт-Петербурга до границы с Норвегией) пересекает множество водоохранных зон. Она имеет следующие особенности: отсутствие электроснабжения; до 40 % территории заболочено или имеются выходы горных пород; чрезвычайно малое (от 0,3 м) превышение полотна дороги над рельефом местности; высокий уровень грунтовых вод. В таких условиях применение локальных очистных сооружений (ЛОС) подземного размещения и с насосной перекачкой стока исключено. Найдено решение [3], которое предусматривает: самотечное движение стока; его сорбционную очистку на многослойном фильтре малой толщины; расположение ЛОС неглубокое или на поверхности земли; «водозаполненное» состояние в рабочем режиме (очистка стоков) и «сухое» в режиме ожидания (включая зимний период).

Вынужденное использование сорбционного фильтра малой толщины (в противоположность нормативно большой) потребовало соответствующего обоснования. Постановочные эксперименты показали: сорбционная очистка на слоях малой толщины имеет право на жизнь; сорбционный фильтр должен быть многослойным, как минимум трехслойным; один из сорбентов должен обладать высокой сорбционной емкостью, но может иметь плохую кинетику; второй сорбент мо

жет обладать невысокой сорбционной емкостью, но должен иметь хорошую кинетику; требуется также третий слой сорбента – страховочный.

Перспективным для фильтра с такими показателями оказалось использование полимерного (пенополиуретан), органического (модифицированный торф) и минерального («Новосорб») сорбентов. Для качественной и количественной оценки возможностей этих сорбентов мы воспользовались методами и средствами хорошо развитой теории динамики сорбции.

КИНЕТИКА СОРБЦИИ НЕФТЕПРОДУКТОВ

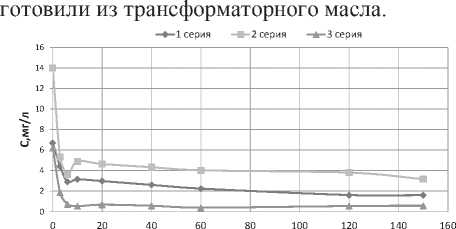
Кинетику сорбции определяли экспериментально. На рис. 1 представлены данные о содержании нефтепродуктов в пробах раствора объемом 400 мл после контакта с сорбентом «Новосорб», d ≥ 1 мм, масса 3 г при t = 20 ºС. Модельный раствор концентрацией 6–133 мг/л

t, мин

Рис. 1. Кинетические кривые сорбции нефтепродуктов на «Новосорбе»

Примерно 20-минутная продолжительность установления равновесия в системе раствор – сорбент свидетельствует о внутридиффузионной природе сопротивления сорбции нефтепродуктов. В близких условиях проведены эксперименты с пенополиуретаном и торфом. Здесь равновесие в системе раствор – сорбент установилось примерно за 40 и 20 мин. соответственно.

РАВНОВЕСНАЯ СОРБЦИЯ НЕФТЕПРОДУКТОВ

Изотермы сорбции «Новосорба» (d ≥ 1 мм, t = 20 ºС, Т = 20 мин.), пенополиуретана (d = 3 х 2 х 1 см, t = 20 ºС, Т = 40 мин.) и торфа (волокна, t = 20 ºС, Т = 20 мин.) показаны на рис. 2.

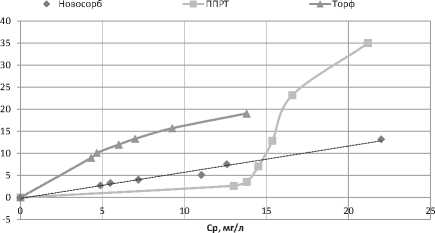
Рис. 2. Изотермы сорбции нефтепродуктов на «Новосорбе», пенополиуретане и торфе:   – торф (волокна, T = 20 мин.); –

«Новосорб» (фракция 5–6 мм, контакт 20 мин.);   – пенополиуретан (фракция 3 х 2 х 1 см, t = 20 ºС, T = 40 мин.)

Вид изотерм свидетельствует о линейной зависимости равновесной сорбции от концентрации нефтепродуктов в изученном диапазоне концентраций. Изотерма сорбции на пенополиуретане имеет вогнутый характер, максимальный коэффициент распределения достигается при максимальной концентрации С _р = 21,2 мг/л. Равновесная величина а = 70 мг/г. ^р

ДИНАМИКА СОРБЦИИ

Лабораторный фильтр высотой 13 см и массой 13,9 г включает слой пенополиуретана (3 см, 1,23 г), торфа (6 см / 5,6 г), еще один разделительный слой пенополиуретана (1 см / 0,38 г), «Ново-сорб» (3 см / 6,7 г).

Со скоростью 1 м/ч фильтровали модельный из объема воды, большей объема сорбента примерно в 10 раз при проскоке на уровне 5 мг/л.

ОЧИСТКА РЕАЛЬНОГО СТОКА НА МОДЕЛИ МНОГОСЛОЙНОГО ФИЛЬТРА

Возможность очистки стока (растопленные образцы снега с придорожного полотна) испытали на модели многослойного фильтра. В пробах исходного и очищенного стока контролировали нефтепродукты, взвешенные, цветность, мутность, рН. Из эксперимента следует, что при скорости фильтрования 4 м/ч и исходной концентрации нефтепродуктов 22,0 мг/л комбинированный слой фильтра обеспечивает очистку до 0,5 мг/л не менее 5 л нефтесодержащего стока. Одновременно удаляются взвешенные (с 1015,0 до 3,0 мг/л), снижается рН (с 7,95 до 7,74), повышается цветность воды (с 67 до 126 градусов).

Из анализа экспериментальных данных можно сделать следующие выводы.

ПЕНОПОЛИУРЕТАН

• 1.    Изотерма сорбции на пенополиуретане имеет вогнутый характер. При вогнутой изотерме имеется стадия «зарядки» – накопления на

  поверхности сорбента монослоя нефтепродукта, когда коэффициент распределения Г мал и отмечаются значительные проскоки загрязнителей. Далее идет аутогезия («самослипание»), то есть

  
  

  способность поглощать загрязняющие вещества (ЗВ) за счет прочной адгезии на поверхности одного и того же вещества. По данным экспериментов на стадии «зарядки», Г = 260, при переходе к стадии аутогезии Г увеличивается до 3300 и выходная концентрация резко снижается.

• 2.    Из кривых кинетики на пенополиуретане следует, что концентрация нефтепродуктов в растворе снижается примерно за 40 мин., тогда как на двух других сорбентах (торф и «Ново-сорб») – примерно за 20 мин.

Таким образом, пенополиуретан проходит стадию «зарядки», пока концентрация нефтепродукта на поверхности сорбента не достигнет порядка 7 мг/г. При этом возможны значительные проскоки нефтепродукта. На следующей стадии ауто- раствор нефтепродуктов с С0 20–40 мг/л. Данные о концентрации на выходе приведены на рис. 3.

гезии коэффициент распределения резко увеличивается, проскоковая концентрация снижается.

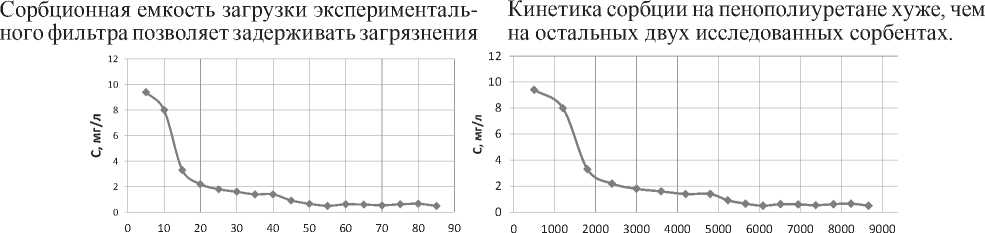
t, мин

V, см3

Рис. 3. Выходные кривые поглощения нефтепродуктов сорбционной загрузкой модельного фильтра: h = 13 см, V = 1 м/ч, C исх нп = 40 мг/л

ТОРФ

• 1.    Изотерма сорбции на торфе в исследованном диапазоне концентраций имеет слабо выраженный выпуклый характер. Если аппроксимировать ее линейной, то коэффициент распределения Г равен 1380, что в 2,4 раза меньше, чем для пенополиуретана на стадии аутогезии.

• 2.    Кинетика сорбции для торфа значительно лучше, чем для пенополиуретана.

Сделаем сравнительную оценку величин кинетического коэффициента для этих сорбентов, исходя из внешнедиффузионной модели сорбции. Для объема раствора V и массы сорбента m условие материального баланса сорбируемого вещества имеет вид:

VC + ma = VC ₀,              (1)

где С – концентрация в растворе в момент времени t , a – концентрация в фазе сорбента в момент времени t , C ₀ – концентрация в растворе в начальный момент времени t = 0.

Уравнение кинетики сорбции запишем для случая больших коэффициентов распределения Г, когда можно пренебречь влиянием сорбционного торможения в сорбенте (это эквивалентно случаю прямоугольной изотермы):

da

— = р С , если a <  a ₀, dt

где а ₀ – емкость сорбента.

Вместе с уравнением баланса (1) получим систему, исключая из которой а , получим обыкновенное дифференциальное уравнение:

^^^^^s

V dС

--= р С, если a <  a ₀, m dt

Эта величина определялась для m = 2,1 г, поэтому для расчета на 0,8 г сорбента пенополиуретана мы примем величину 0,41 х 0,8/2,1 = 0,16.

Поскольку Р _пп/ Р _т = 2, то р пп = 0,08 с^-1.

«НОВОСОРБ»

• 1.    Изотерма сорбции близка к линейной, причем коэффициент распределения, равный отношению равновесных концентраций в сорбенте (измеренный в мг/г) к равновесной концентрации в растворе (измеренный в г/мл, что эквивалентно отношению г/г), равен 560.

• 2.    Кинетика сорбции, как следует из кинетических кривых, аналогична кинетике на торфе, то есть примерно в два раза лучше, чем на пенополиуретане.

Таким образом, минеральный сорбент «Но-восорб» обладает самой малой емкостью из трех изученных сорбентов, однако имеет хорошую кинетику сорбции, поэтому может быть использован как «финишный» сорбент в многослойном фильтре.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ПРОЦЕССА ДИНАМИКИ СОРБЦИИ ПРИ ПРЯМОУГОЛЬНОЙ ИЗОТЕРМЕ

Лимитирующим компонентом избран нефтепродукт. Для большей математической ясности рассмотрен предельный случай – динамика при прямоугольной изотерме, лимитирующая стадия кинетики – внешняя диффузия. Модель динамики сорбции при прямоугольной изотерме имеет вид [1]:

решение которого при условии C (0) = C ₀ имеет вид:

6 С 6 a „ v — + — = 0, 6 x    6 1

С = С ₀ехр(- Р mt / V) ,           (4)

которое представим в виде:

ln( C / C 0 ) = - p mt / V.            (5)

Отсюда следует, что если для достижения фиксированного отношения C/C0 для двух сорбентов (сравниваем пенополиуретан и торф) требуется разное время (в наших опытах для пенополиуретана требуется 40 мин., для торфа – 20 мин.), то величина p для пенополиуретана должна быть в два раза меньше, чем для торфа, а именно р пп/рт = 40/20 = 2.

Таким образом, торф обладает емкостью в 2,5 раза меньшей, чем пенополиуретан, но в 2 раза лучшей кинетикой сорбции.

Воспользуемся данными кинетических опытов для расчета р _пп и р _т.

Для времени сорбции 20 мин. С = 2,6 мг/л, при С ₀ = 36,6 из формулы (5) при V = 400 мл и m = 2,1 г получим:

Р т = 0,41 с^-1.

6 _a  J P C , если a <  a ₀

6 1   [ 0, если а = а ₀

Здесь (6) – уравнение баланса в слое сорбента, (7) – уравнение внешнедиффузионной кинетики.

Введены следующие переменные: С ( x , t ) – концентрация сорбируемого компонента в растворе, а ( x , t ) – концентрация сорбируемого компонента в сорбенте (в неподвижной фазе), х – координата вдоль слоя сорбента, х = 0 – входное сечение, t – время ( t = 0 – начало процесса сорбции), β – внешнедиффузионный кинетический коэффициент, С ₀ – концентрация сорбируемого компонента в исходном растворе, а ₀ – емкость сорбента (в расчете на единицу объема слоя сорбента). Концентрации С и а зависят от координаты вдоль слоя сорбента х и t .

Прямоугольный характер изотермы проявляется в том, что поглощение вещества сорбентом происходит с постоянной скоростью до тех пор, пока не будет исчерпана емкость а ₀.

Решение этой системы выполняем при следующих условиях:

C (0, t ) = C 0 ,                    (8)

C ( x , 0) = a ( x , 0) = 0.                (9)

Первое условие означает, что во входное сечение слоя сорбента поступает раствор, содержащий сорбируемый компонент в постоянной концентрации C 0 , по второму условию сорбент свободен от сорбируемого компонента в начальный момент времени.

Решение сформулированной краевой задачи известно и имеет вид [1]:

при t <  a ₀ / (вС₀) С = С ₀ exp(- вх / v ), a = PtC ₀ exp(- ex / v ),(10)

при a 0 / ⁽ PC 0 ) <  t <  a 0 / ⁽ PC 0 ) ⁺ xa 0 / ^{( V}C 0 ) C = aC ₀ / a ₀ = C ₀ exp(- Px / v + PtC ₀ / a ₀ - 1),

при t > a₀ / ( PC ₀) + xa ₀ / ( vC ₀) C = C ₀, a = a ₀, (12)

Можно записать это решение в более простой форме, перейдя к безразмерным переменным:

u = С- , q = a , X = ^в , T = aC⁰t .    (13)

C о         a о           v           ^a о

Здесь и и q - безразмерные концентрации в растворе и сорбенте, Х и Т - безразмерные координата вдоль слоя и время. Тогда решение (5)-(7) примет вид:

u ( X , T ) = exp(- X ), q ( X , T ) = T exp(- X ) при 0 <  T < 1, u ( X , T ) = q ( X , T ) = exp(- X + T - 1) при 1 <  T < 1 + X , ⁽¹⁴⁾

u ( X , T ) = q ( X , T ) = 1 при T > 1 + X

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ПРОЦЕССА ДВУХСЛОЙНОГО ФИЛЬТРА

Первый и второй слои состоят из сорбентов емкостью а ₀₁ и а ₀₂, кинетическими коэффициентами в 1 и в ₂, толщинами слоев 1 1 и 1 ₂. Выше отмечалось, что пенополиуретан на стадии аутосорбции обладает самой высокой емкостью, однако его кинетика примерно в два раза хуже, чем у торфа.

Представляет интерес выяснить: является ли двухслойный сорбент более эффективным, чем однослойный?

Поскольку по конструктивным соображениям сорбционные фильтры для автодороги М-18 «Кола» должны иметь слои малой толщины, возможна ситуация, когда уровень проскока, если заполнить весь фильтр 1 первым сорбентом, может не отвечать требованиям глубины очистки: вследствие плохой кинетики (малости коэффициента в ] ) выходная концентрация, в соответствии с (5) равная С = С ₀ехр(- в ₁ 1 / v), может оказаться больше требуемой С _п.

Для упрощения требуемый уровень С _п / С ₀ обозначим через е = С _п / С ₀. В фильтре только из пенополиуретана возможно ехр(- в 1 1 / v ) >  е .

Если фильтр целиком заполнен вторым сорбентом, то, поскольку в ₂<  в 1 , условие проскока может быть выполнено, так как ехр(- в 1 1 / v ) > ехр(- в ₂ 1 / v ), если различие между в ₂ и в 1 будет значимым.

Для приведенных коэффициентов в имеем: в 1 = 0,08 с^-1, в ₂ = 0,16 с^-1.

Если слой в 6 см будет состоять только из пенополиуретана, а скорость равна 0,1 см/с, то уровень проскока будет равен ехр(-4,8) = 0,0074.

Если слой в 6 см будет состоять только из торфа, уровень проскока будет равен ехр(–9,6) = 0,000054.

Поскольку емкость торфа значительно меньше емкости пенополиуретана, используя решение (14), сравним время защитного действия для двух случаев:

• 1.    Фильтр состоит только из торфа толщиной 1 ;

• 2.    Фильтр состоит из пенополиуретана толщиной 1 1 и торфа толщиной 1 ₂.

Для уровня проскока е время защитного действия t з ¹ в соответствии с решением (11) будет равно:

t i = a^i+ +in _e )+ ао^ . (15) ^в 2 C о C о ^v

Во втором случае на входе во второй слой поддерживается постоянная концентрация С ₁₀, данная формулой:

С _ю = С 0 ехр(- р , 1 , / v ). (16)

На рис. 4 представлено распределение концентраций загрязнений по слоям сорбента двухслойного фильтра.

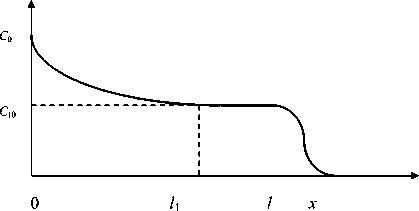
Рис. 4. Распределение концентрации C ( x , t ) по загрузке из двухслойного фильтра

Время защитного действия во втором случае будет даваться формулой:

1 1¹ = a , 2     ₊ ln C p ) ₊ a °₂^{( 1} / J

^J   в C J    Сю    C_m v

.

Входная концентрация во второй слой по (16) будет равна С ₁₀= С₀ехр(- в ₁ 1 1 / v ). Важно знать, при каком соотношении сорбционных параметров отношение t з ¹¹/ 1 з ¹ будет больше единицы.

Обозначим это отношение через т . Используя выражение (17) для С ₁₀, а также полученные формулы (15) и (17), после несложных преобразований получим выражение:

, , ДА вк 1 + in 8 +    + ^2^- т = exp X,

vv

1 + in 8 + в 1

.

v

Поскольку длины слоев l ₁ и l ₂ выбираются из условия обеспечения проскока ε , то должно выполняться условие:

е = exp( - ^ 1 -     ) .            (19)

vv

Заменяя ε в формуле (18) по (19), получим т = exp X1------1------.           (20)

• 1    + X ( ^в - 1)

в

При длине первого слоя 3 см X ₁ = 2,4; поскольку β ₂/ β ₁ = 2, то τ = 3,41.

Итак, комбинированный сорбент, у которого β2 = 2β1, l2 = l1, выходная концентрация в е = exp(—1-1- —2-А) = exp(-7,2) = 0,00063 на поря-vv док меньше, чем для слоя l1 целиком из первого сорбента ε = 0,0074. Увеличивается время защитного действия по сравнению с однослойным вариантом, когда весь слой заполнен вторым сорбентом τ = 3,41.

Эксперимент и анализ модели дали практические выводы:

• 1.    Сорбционные методы очистки дорожных ливневых и талых стоков в целях предотвраще-

• ния загрязнения окружающей среды нефтепродуктами имеют право на жизнь.

• 2.    Равновесие в системе раствор – сорбент устанавливается для торфа и «Новосорба» за 20 мин., для пенополиуретана – за 40 мин., то есть торф и «Новосорб» обладают более высокими кинетическими свойствами, чем пенополиуретан.

• 3.    Наибольшей сорбционной емкостью в изученном диапазоне концентраций обладает пенополиуретан.

• 4.    Двухслойный фильтр из пенополиуретана и торфа эффективнее однослойного: больше время защитного действия, выше кинетика с меньшей проскоковой концентрацией.

• 5.    Трехслойный фильтр (пенополиуретан, торф и «Новосорб») снижает концентрацию нефтепродуктов в 40 и более раз, удаляет взвешенные вещества, снижает pH.

Полученные рекомендации позволили разработать проекты (совместно с ООО «Геолайн»), изготовить (совместно с ООО «Металлист»), смонтировать (совместно с ООО «Технострой») и передать в штатную эксплуатацию около 100 ЛОС в водоохранных зонах мурманского участка автодороги М-18 «Кола» [2].

* Работа выполнена при поддержке Программы стратегического развития (ПСР) ПетрГУ в рамках реализации комплекса мероприятий по развитию научно-исследовательской деятельности на 2012–2016 гг.