Математическое моделирование и расчет распространения направленных импульсов в однородных поглощающих средах

рье от исходного сигнала и представляет собой набор синусоидальных сигналов разной амплитуды и фазы.

ГО

S( О ,j ® ) = F[p(O,t)] = J p( О ,t )e ~ j ® dt =

_               _           -”                  (2)

= iS _X (O, j ® ) + jS ( (O, j ® ) + кS _z (O,j ® )

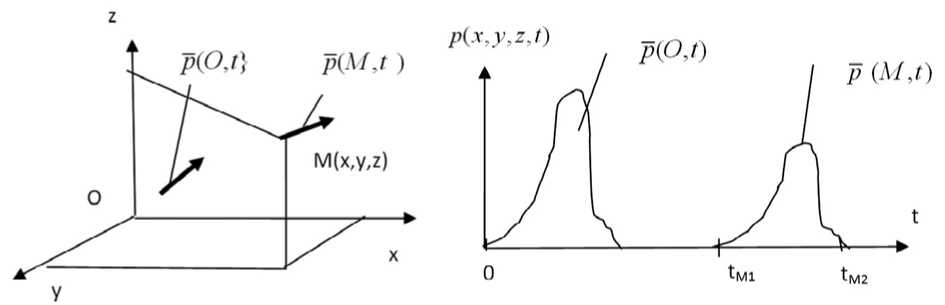
Изменение амплитуды и спектрального состава зондирующего импульса, прошедшего через исследуемую среду, дает информацию о среде или объекте. Распространяясь в среде, импульс можем в общем случае изменять форму и направление, что определяется свойствами среды. Рассмотрим распространение импульса в однородной среде, в которой направление импульса не изменяется.

В работе [5], на основе анализа работ [2,3], получено аналитическое выражение, моделирующее распространение импульса в однородной поглощающей среде, которое имеет вид:

P ( r,t ) = 1- ^ГО S ( O, j ® ) e ^j [ ® t ^{- k ( j} ® ) ^ ^{г ]} d ® = 2 n

-ГО

1 ГО ГО                        Г             _          -I

= 21- j j p ( O,j ® 'y j ^[( t ^-t ) ® ^- k ⁽ j ® ) ^ ^{г ]} d r d ®

-ГО

-ГО

где r = i ( x - x₀ ) + j ( ( - (₀ ) + к ( z - z₀ ) - радиус-вектор заданной точки пространства относительно точки излучения,

а)

б)

Рис. 1. Иллюстрация к постановке задачи распространения импульса в неподвижной среде

к ⁽ j to ) = i X ^{( (} j to ) + jk_y ^{( j} to ) + к k z ^{( j} to ) = = k to ) - jk "( to )

– волновой вектор, kx(jto ) = k((to) + jk "x(to), ky (jto ) = k'y (to) + jk'y(to) , kz (jto )= k Z (to ) + jk "z(to ) k '(to) = ik '(to) + jk '(to) + kk '(to), k"( to) = Tk "(to) + 3k "(to) + kk "(to).

При этом k' ( to ) - определяется фазовой скоростью распространения энергетической волны в среде [2]:

k' ( to ,R ) =

to _ о> к_ф ( to )

V (to) V (to) 2 ;

k"( to ) = a ( to ) — коэффициент поглощения среды.

Здесь и далее следует различать j и к — как орты декартовой системы координат, k - как волновой вектор, j = V—1 ;

r = r | = V ^{( ( - (} 0^{) 2 + (} y ^- y 0^{) 2 + (} z ^- z 0^{) 2} , ⁽⁶⁾

k (jto )• r = (( - (o)kx (jto)++ (У - Уо )ky (jto) + (z - zoo)kz (jto) (7)

– скалярное произведение волнового вектора на радиус вектор заданной точки пространства, т - формальный параметр интегрирования.

Отметим, что в классической теории волновых процессов в не поглощающих однородных средах волновой вектор определяет число длин волн, умещающихся на единице длины [1/м]. В поглощающих средах волновой вектор также имеет размерность [1/м], однако здесь его физическая трактовка больше согласуется с комплексным коэффициентом поглощения пакета энергии распространяющегося в среде, которая по аналогии с электричеством может быть актив- ной, проявляющейся, например, в виде нагревания среды, и реактивной, определяемой электромагнитными или квантово-механическими процессами в зоне следования импульса.

Учитывая (4) можно записать:

to to

p ( _r, t ) = — J J p ( O,T ) e-^{k ,( to}^r e^{j [(} t ^{- т ) to - k} '^{( j to} ) - ^{г ]} dTdto. (8) ^{2 n} -to-to

Отметим, что в общем случае для неоднородных сред волновой вектор является функцией координат, что приводит к тому, что импульс может двигаться по криволинейной траектории и менять свое направление. В однородной среде импульс не может изменить свое г о нап р авления, поэтому вектора p ( O,t ) ,k ( j to ) ,k' ( to ) ,k" ( to ) ,r,p ( r,t ) колле-ниарны, то есть совпадают по направлению. Из коллениарности следует, что k '( to ) • r = k ' ( to ) r , k'' ( to ) • r = | k '' ( to )| r

Тогда для однородных сред выражение (8) можно переписать в виде:

p ( r,t ) = — J to p ( O, T ) e - k^Я'^jt " ^т "' k ^{j )} r ¹ d T d to . (9)

^{2 n} -to-to

Выражение (9) связывает параметры импульса, появившегося в точке “r” пространства c параметрами импульса, запущенного в точке “О” . Оно определяет каждую координатную составляющую импульса:

1 to to px,(y),(z)(r, t) = — J J px(y),(z)(O,т)x

^{2 П} -to -to

- k "to ) r j [ ( t - т ) to -I k '( j to )| r ]

x e e             d T d to

Сигнал, вычисленный по формулам (3), (9), (10) в общем случае является комплексным:

p ( r,t ) = Re ( r,t ) + jIm ( r,t ) . (11)

Как указано в [2, 3], физический смысл следует придавать действительной части выражения (13). Однако при анализе энергетических характеристик импульса не следует отказываться от мнимой составляющей выражения (11).

Прошедший через однородную среду импульс, в общем случае изменяет свою форму, скорость и в точке приема несет в себе информацию о свойствах среды или об объекте. При этом важно знать амплитудный спектр принятого импульса, который определяется как прямое преобразование Фурье:

S ( r , j ® ) = F [ p ( r , t )] .         (12)

Следует отметить, что, как правило, все приемники импульсных сигналов, являются координатно-ориентированными, поэтому важно вычислять координатные составляющие прошедшего через среду импульса и соответствующие им амплитудные спектры S_x ( r,j ® ) , S y ( rr,j ® ) , ^S z ^{( r,}j ® ) .

Приведенные выражения, определяющие в общем виде форму и местоположение зондирующего импульса, прошедшего через среду, являются математической основой для исследования сред и объектов методом импульсного зондирования. Задавая параметры среды, в виде волнового вектора, определяющего коэффициент поглощения и фазовую скорость распространения, с учетом направления излучающего импульса можно численно моделировать прохождение импульса в пространстве или объекте, наблюдать искажение его формы, определять место и время прибытия в какую-либо точку пространства.

Выражение (10) является скалярным и определяет каждую координатную проекцию импульса, пришедшего в заданную точку среды как функцию времени и координат. Формулы (3), (9) и (10) предполагают, что импульс может появиться только в той точке пространства, которая лежит на направлении распространения излученного импульса.

Для простых однородных сред, без частотной зависи мости ( диссипации) волнового вектора k ( ® ) = k ' - jk " выражение (9) примет вид: P ( r,t ) = —— J J P ( О т Y ^[( t -^т ) ®- k ⁽ j ® ) r ^] d i d ® .(13)

-J - J

- kr

Здесь сомножитель e определяет изменение амплитуды сигнала по координатам, все остальное описывает форму импульса во времени в заданной точке r.

Рассмотрим пример расчета распространения электромагнитного импульса в однородной среде, выпущенного из начала координат O(0,0,0). Для электромагнитных сигналов в неограниченной однородной среде волновой вектор является скаляром, зависит от частоты и определяется выражениями [1, 4]:

k ( ® ) = ^ ®р ( ® )p₀ [ ё ( ® £ ₀ ® - j c ( ® ) ] =

= k' ( ® ) - jk'' ( ® )                          ^,(14)

где р0 =1,25663740-6 Гн/м, £0 =8,85416Л0-12 Ф/ м, ^о , Мо , £ удельная электрическая проводимость, относительные магнитная и диэлектрическая проницаемости среды соответственно, рр0®( \С2 + E2s02 ®2 + ££0®)

k = 1------------------------------- коэффициент распространения;

ММ ₀ ® ( \^^: + ^£ 0 ® - ££ ₀ ® )

k =

–

коэффициент затухания.

Фазовая скорость определяется по формуле:

V ф =

® k

2 ®

2     2 2 2 . (17)

ЦЦ ₀( £ ₀ £® + ^ + ££ ₀ ® ) ^х '

Определим вид функции, которая описывала бы форму сигнала в некоторой точке { х,y,z } . Для простоты сделаем допущение, что зондирующий сигнал имеет только одну координатную составляющую p ⁽ O,t ) = iP x ^{( o,t} ) , направленную только вдоль оси х . При расчете воспользуемся формулой (10).

Для проверки полученных выражений рассмотрим простейший случай, когда проводимость среды с т = 0 и волновой вектор содержит только действительную часть:

k ( j ® ) = ®^Р® ,

с – скорость света в вакууме.

Подставив данное выражение в формулу (10), мы приходим к следующей форме записи:

1 J J

Px (r,t )=5“f J Px (O,T )e :n -J-J did® =

J

J

= 4" J J Px ^{( o, t} ) e 2 П

-J

-J

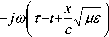
J               ( x

= J P ( О, т ) ® т - t — урё I d i =           (19)

x

-J           V \ c 7 /

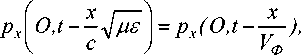
где V o = с /V p£ — фазовая скорость распространения сигнала.

То есть в данном случае сигнал приходит в искомую точку с задержкой, определяемой фазовой скоростью распространения электромагнитных импульсов в рассматриваемой среде, но без затухания и искажения формы, что хорошо известно и вполне очевидно.

Рассмотрим общий случай, когда волновой вектор имеет действительную и мнимую составляющие и описывается выражениями (14)-(16). Функция (10) примет следующий вид:

Учитывая, что k' x (0 ) = 0 и k" x (0 ) = 0 , выражение (25) приводится к виду:

1 го го

Px (r,t) = ^~J I Px (O,T)x

2 ^П -го -го

X e ⁽⁽ t ^T ) ® ^-( k x ⁽ ® ^{)- jk} x ⁽® )) ^x ) d _T d _to

ф_х ( t,0 ) = lim —sin ® t cos0 ® ^ 0 ®     2

V

A t

= 2 . (26)

Таким образом, приближенно интеграл (23) вычисляется по формуле:

Зададим зондирующий сигнал в виде прямоугольного импульса:

An fx(t) ~ - (Tx (t,0)+Ё (Tx (t, iA®)+ n          i=1

0,t <  0,

p x ( O,t ) = « A,0 <  t < A t,

( •.     T ( t,n A® ) + T ( t, - n A® )V (27)

+ T _x ( t, - i A® )) -         ^2^ ¹ l A® .

0,t >  A t.

Подставим это выражение в (10) и после преобразований получим:

1 го At px ( r, . )- П JJ Ae

-го 0

d i d ® =

го

= A!

П

-го

e - k x ( ® ) x

®

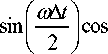
- л го - k ' ( ® ) x jA Г ex' ^п -го ®

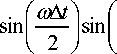
x    ®At ] , t® - k,(®) x--d®+

x

^{2 7}      (22)

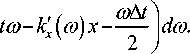
Для определения искомой формы результирующего сигнала используется действительная часть выражения (22):

го

f, ( t ) = A J

П

e

-

- k x ⁽ ® ) x

®

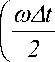
-го x cos

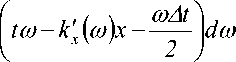
Решение задачи возможно только методами численного интегрирования. Приближенное вычисление значения интеграла в выражении (23) осуществляется по методу трапеций. Обозначим подынтегральную функцию как:

T x ^{( t} , ® ^{) =}

_e ^{- k} x ⁽® ) ^x

®

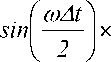
x cos I t ® - k x ( ® ) x -

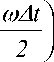
Оценка значения функции (24) в точке ® = 0 определяется через предел:

e - kx(®)x фх (t,0 )= lim-------

® ^ 0   ®

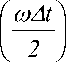
Г           ,   ®A t )           (25)

x cos I t ® - k_x ( ® ) x --I

Из условий допустимой погрешности интегрирования найдем значения n и A® .

Величина шага интегрирования Ato определяет погрешность численного вычисления интегралов периодических тригонометрических функций. Например, для обеспечения погрешности вычисления A <  1% тригонометрической функции с периодом Т достаточно, чтобы шаг интегрирования был равен A® = Т 20 .

Период функции sin ( ®A t/2 ) :

Т sin

4 п

1 7 ■

w                     1.x ,, к      ®At )

Период функции cos I t ® - k_x ( ® ) x — l

определяется через приближенное значение параметра k'x ( ® ) :

k x ⁽ ® ) =

Д^ ₀ ® ( \[^ ² + £ 2 5 02 ® + ББ 0 ® )

ЦЦ0®ОО

—,® <<

V 2££

®^JU ₀ ££ ₀, ® >>  °- . ^££ ₀

Таким образом, оценить период можно для обоих случаев:

T cos ( ® )

2 n

О

t

A t

x

2 n

MHq°

2 ®

, ® <<      ,

^££ 0

t

A t

, ®

°_. (30)

^x №a ^££ 0

^££ 0

Из формулы (29) видно, что шаг интегрирования в общем случае является функцией от частоты:

_Да(_а ) = min l X in T s H ] 20         ^.

Таким образом, выражение (27) преобразуется к новому виду, что означает переход к интегрированию с переменным шагом:

f x ^{( t,n} ) ~ A Фх ^{( t}0 ) + Z ( P x ⁽ t, ^to i - 1 + ^ДА<Р - 1 )) +

^П        i = ¹                     (32)

+ P x ( t. щ - i ^- M^ - i Ш/М м 1 ))

Следующим действием является определение n или границ интегрирования. Для этого необходимо вычислить значение n , после которого вычислением оставшейся части интеграла (23) можно пренебречь. При вычислении значения функции (32) значение n можно не задавать заранее, а определить его по ходу выполнения вычислений.

При достаточно больших значениях а составляющая волнового вектора к Х ( а ) практически не меняется:

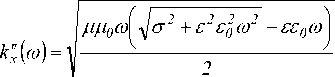
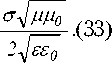
Обозначим Да_т приращение частоты, соответствующее периоду T _sin -T_cos ( а ) и, подставив их, рассмотрим следующий интеграл:

а а + Да

I x ( t ) = A J ^п а

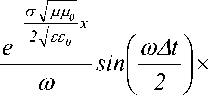
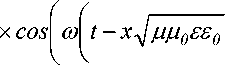
Д )]

^{2 )} )

При бесконечном увеличении значения а интеграл (34) стремится к 0, поэтому ряд (32) сходится при n ^ да и может быть вычислен с заданным требованием точности. Если значения функции (32) практически не отличаются при n и n + Да _т / Да , то интеграл (23) можно считать вычисленным.

Общий алгоритм вычисления формы результирующего импульсного сигнала, прошедшего через среду при зондировании её сигналом с заданными характеристиками имеет следующий вид.

Шаг 1 . Задание границ отображения графика t_l и t _r , определение количества точек m на графике, вычисление шага приращения ^{Д t} = ^{( t}r ^- tl И m ^{- 1} ) .

Шаг 2 . Начальная точка графика t = t_t .

Шаг 3. По формуле (32) вычисляется приближенное значение результирующего сигнала в точке t .

Шаг 3.1 . Задается начальное значение n = 0 .

Шаг 3.2. По формулам (28) и (30) определяются периоды, вычисляется приращение Да по формуле (31).

Шаг 3.3. Рассчитывается значение функции f x ( t,n ) по формуле (32).

Шаг 3.4. Увеличивается приближение n = n + 1 , соответственно а = а + Да .

Шаг 3.5. Если

| fx ^{( t,}n^{2 )-} fx ^{( t,n} )

меньше

| f x ( t,n )

некоего наперед заданного г , то приближенное вычисление точки считается завершенным. В противном случае возвращаемся к шагу 3.2.

Шаг 4. Аналогично шагу 3 вычисляется значение мнимой части в точке t .

Шаг 5. На графиках отмечаются вещественная и мнимая точки, а также величина модуля сигнала в точке t .

Шаг 6. t = t + Д t . Если t >  t_r , то алгоритм завершается, иначе переходим к шагу 3.

Аналогично можно вычислить мнимую часть выражения (22). Спектр исходного сигнала рассчитывается по формуле прямого преобразования Фурье:

+да

Fucx (а )= J Px (0,t )e-j"*dt = да

,^ДД           2 a . аД t ⁽³⁵⁾

= A\e j dt =---- sin ----.

о         aAt 2

Учитывая, что результирующий сигнал не имеет аналитического выражения, его спектр вычисляется по табличным значениям:

m ti+1 /\

Sx (r,jO) =Z J (PRe (r,t) + JPxmi (r,t)e-jаtdt = i=0 ti m            ti+1                m            ti+1(36)

= S p Re ( r,t ) J e ^{- j}"dt + j Z P xm ( r,t ) J e ^{- j а ,}dl^

i=0              ti                   i = 0t где PRe (r,t) и pxm (r,t) - табличные значения действительной и мнимой части результирующего сигнала, соответственно.

На рис. 2 приведены результаты расчета распространения прямоугольного электромагнитного импульса длительностью Дt = 10-7 сек, амплитуды A = 1, через среду с проводимостью (У = 10-17 Сим, относительной диэлектрической проницаемостью £ = 2, магнитной проницаемостью ц = 1 для точек контроля, находящихся на расстоянии 1 м, 50 м и 100 м от точки излучения. Графики иллюстрируют время прихода импульса в заданную точку, затухание и искажение его формы в зависимости от расстояния. При этом действительная часть импульса соответствует его физическому содержанию, которое наблюдается на экране осциллографа. Мнимая часть позволяет с высокой точностью фиксировать временные параметры импульса (момент прихода и длительность), так как на фронтах импульса его мнимая составляющая имеет острый, явно выраженный экстремум. Причем минимум на переднем фронте, максимум - на заднем. Это дает возможность идентифицировать “тело” импульса при периодических импульсных облучениях. Модуль позволяет с высокой точностью определить энергетические характеристики, вычислить полные, активные и реактивные потери, обусловленные движением импульса в среде.

На рис. 3 показаны результаты расчета прохождения электромагнитным импульсом расстояния 100 м при различных значениях диэлектри- ческой проницаемости среды ( £ = 1, £ = 2, £ = 4 ) и ПОСТОЯННЫХ проводимости ( у = 10-17 Сим) и магнитной проницаемости ц = 1.

Анализ графиков показывает, что диэлектрическая проницаемость среды значительно влияет на скорость движения импульса. С ростом диэлектрической проницаемости время прибытия импульса в заданную точку увеличивается, затухание возрастает, что полностью соответствует аналитическим выражениям (16), (17) и подтверждает правильность разработанной методики расчетов.

На рис. 4 показаны результаты расчета прохождения электромагнитным импульсом расстояния 100 м при различных значениях проводимости среды ( у = 10 - ¹⁰ , _у = jq - ⁵ , _у = ю - ⁴ Сим и постоянных диэлектрической £ = 2 и магнитной ц = 1 проницаемостей. Анализ графиков

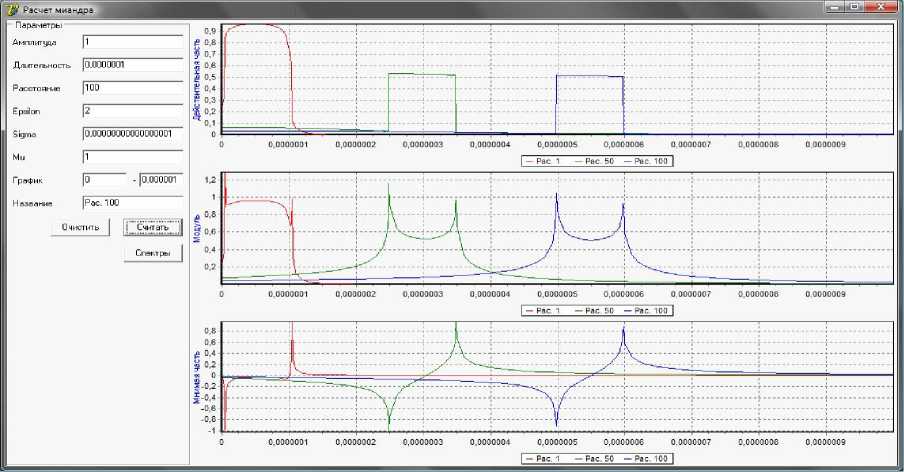
Рис. 2. Составляющие импульса при разных расстояниях до точки контроля

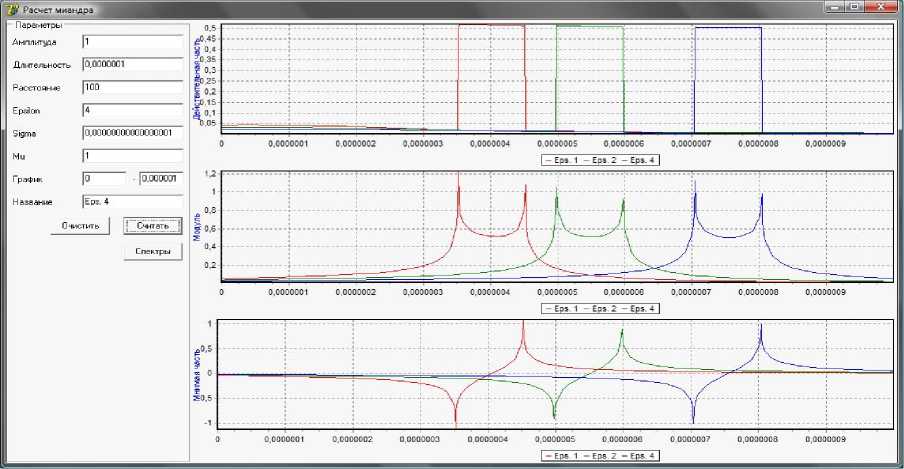
Рис. 3. Составляющие импульса на расстоянии 100 м при изменения £

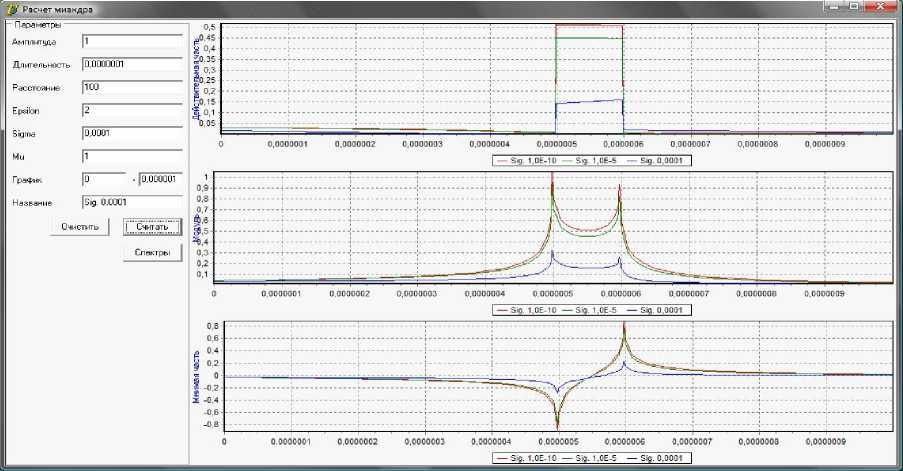
Рис. 4. Составляющие импульса на расстоянии 100 м при изменения σ

показывает, что проводимость среды сильно влияет на затухание сигнала, искажает его форму, но при выбранных значениях практически не повлияло на время прилета импульса, что вполне объяснимо, так как групповая скорость мало зависит от проводимости.