Математическое моделирование и распознавание процессов электрохимической поляризации в системах экспресс анализа металлических сплавов

Электрохимический экспресс-анализ металлических сплавов на основе усовершенствованной импульсной прямой и инверсионной хронопотенциометрии является новым и перспективным методом контроля металлов и сплавов в различных областях техники, технологий, в частности, в машиностроении [1]. Его преимуществами являются экспрессность, простота и высокая информативность. Однако полная реализация преимуществ метода возможна только на основе использования специального математического и алгоритмического обеспечения. Это связано с наличием латентных факторов, влияющих на закономерности протекания электрохимических процессов, лежащих в основе анализа, в частности, сложность структуры металлических сплавов, для которой практически невозможно подобрать адекватную аналитическую математическую модель. В связи с этим представляется необходимым построение специальных математических моделей на основе методов интеллектуальной обработки информации для эффективного решения задач экспресс-анализа сплавов [2-5].

Одной из задач, из общего перечня решаемых при электрохимическом анализе, является предварительный анализ образцов с целью идентификации преобладающего компонента сплава по графику изменения потенциала - хронопотенциограмме. Хронопотен-циограмма является функцией отклика действия

импульсов тока, протекающего в цепи электрохимического датчика и осуществляющего поляризацию образца в импульсном режиме. В настоящей работе рассматривается применение математических моделей компонентного, кластерного анализов, теории распознавания образов, декомпозиционных методов моделирования (ДММ) [2-5] для решения задачи предварительного анализа образцов.

Подходы моделирования процессов при распознавании сплавов. При построении систем распознавания сплавов можно выделить три основных этапа, связанных с математическим моделированием процессов: 1) определение признакового пространства распознавания по обучающей выборке; 2) автоматическая кластеризация выборок хронопо-тенциограмм H j ; 3) выбор решающего правила распознавания сплавов. Первый этап, с одной стороны, связан со снижением размерности пространства представления хронопотенцио-грамм H j =[ h j _Рк, h jn J , но без потери основной информация о сплаве. С другой стороны, с обеспечением наибольшей различимости образов различных сплавов в полученном пространстве. В признаковом пространстве каждый сплав H j , представляется точкой или образом Y. = [ у_; 1 , к , У т J с минимальным числом параметров m < n . Второй этап связан с получением обучающей выборки и определением самой возможности кластеризации сплавов. Третий этап - это определение перечня математических условий, позволяющих с требуемой точностью отнести образ сплава Y . , а, следовательно, и сам сплав к одной из возможных групп (кластеров).

Определение признакового пространства реализуем на основе ДММ, компонентного разложения [3], позволяющего выделить основные составляющие графиков Hj путем преобразования выборки {Hj}, j = 1, N со взаимно коррелированными координатами в образы Yj с линейно независимыми координатами:

Y j = V T H (1)

где V - матрица настраиваемого линейного ортогонального преобразования. Преобразование (1) является декоррелирующим и каждая координата y j образа Y j линейно независима одна от другой, а, следовательно, правомерно предположить, что каждая координата несет свою информацию о форме процесса H j и связана со своей составляющей сплава. Восстановление процесса H j по образу Y j возможно согласно дМм [3]:

Hj=2 y,'V.+ Qj - i=1

где V i - ортонормированные столбцы матрицы преобразования V или настраиваемые базисные функции, по которым разложен процесс H j ; Q j - вектор практически неизменной величины (изменчивость его координат от j мала).

Базисные функции V , i = 1, n вычисляются по выборке { H j } [2, 3, 5], как собственные векторы матрицы выборочных ковариационных моментов K:

КУ=УЛ,          (2)

где Л - диагональная матрица собственных чисел матрицы K:

^ 1 0

...

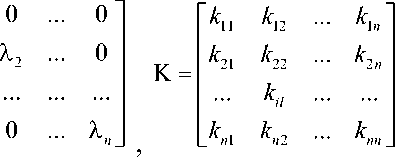
ka=м[(Hj-Hi)(Hj-Hi)] j=1,n ,                     , где M - знак усреднения по индексу j; H i , Hj - среднее значение i и j координат по выборке {Hj}; V=[V1 V2 ... Vn];

Число столбцов матрицы V равно n , однако только малая часть или m из них определяет изменчивость процесса H j . Данные m столбцов матрицы V выбирают по соответствующим наибольшим собственным числам X _i так, чтобы:

nn

^/ V; <_

i = m + 1           i = 1

.

Величина 5 определяет допустимую погрешность распознавания графиков H j или кластеризации. В большинстве практических задач достаточно выбирать 5 = 0,1 ^ 0,02. Использование ДММ для формирования признакового пространства обеспечивает: 1) наилучшую разделимость кластеров (образов) различных сплавов в построенном признаковом пространстве по сравнению со всеми возможными ортонормированными пространствами; 2) адаптивность признакового пространства к изменениям кластеризуемых графиков H j , что позволяет производить настройку системы на распознавание тех или иных сплавов, а также самообучение в процессе работы.

Автоматическую кластеризацию выборок хронопотенциограмм удобно проводить методом k групповых средних [2]. В качестве решающего правила в устройстве распознавания сплавов удобнее всего использовать методы линейных разделяющих функций или непараметрическое правило kNN-ближайших соседей [2, 5]. Эти подходы не требуют знания многомерной плотности вероятности распределения образов в кластерах. При распознавании могут использоваться различные метрики, что улучшает распознавание в случае несферических (эллипсоидальных, плохо разделимых или иных) кластеров. Общий вид линейной решающей функции для двух кластеров ю 1 , ш₂ задается формулой [2]:

m d (Yj ) = 2 w^M wm+1

i = 1

I >  0, если Y. g ш;

= WY. + w J           j ¹

j m [< 0, если Yj g to2, где Wi - весовые коэффициенты, определяемые по стандартным алгоритмам.

Экспериментальные исследования. Экспериментальную проверку изложенных подходов моделирования и распознавания проводили, используя 30 типов сплавов железа, никеля, хрома, меди, титана, молибдена, вольфрама, ниобия, золота, алюминия, цинка, делящиеся по преобладающему компоненту на 19 классов. Цель проверки - выявление работоспособности перечисленных методов при распознавании хронопотенциограмм по преобладающему в сплаве элементу. В результате импульсной поляризации с использованием устройства [1] получили массив H=[H1,...,HN] хронопотенциограмм образцов (рис. 1). Для устранения влияния случайных помех применяли к H медианную фильтрацию 5-го порядка и сжатие массивов, т.е. сокращение числа отсчётов в соответствии со спектральным составом [2]. В соответствии с (2) определили собственные значения Л и собственные векторы V матрицы выборочных ковариационных моментов K (см. рис. 2).

По физическому смыслу V 1 - наиболее значимый собственный вектор, соответствует активному растворению с образованием ионов металлов в электролите, V ₂ и V 3 - пассивации и области транспассивности. Согласно (3), получаем 5 <0,01для 3-х собственных векторов и 5 <0,02 для 2-х, поэтому возможно рассмотрение как 2-х, так и 3-мерного признакового пространства. На рис. 3 приведена кластеризация всех образцов в 2-мерном пространстве собственных векторов V 1 , V ₂. Многие из классов сплавов имеют сложную и взаимопроникающую структуру, что соответствует сложному характеру анодного растворения многокомпонентных сплавов, в котором в зависимости от сочетания компонентов возможны как базовые типы процессов, так и их смесь.

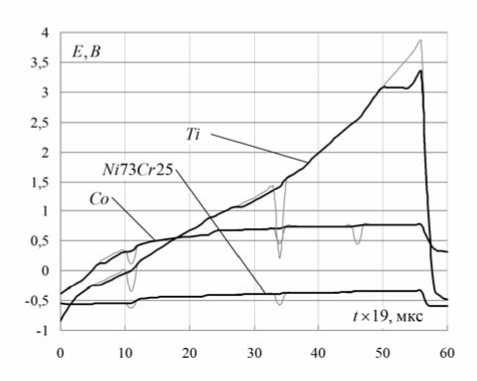
Рис.1. Примеры хронопотенциограмм сплавов

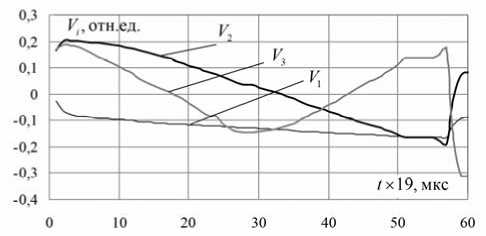
Рис. 2. Три первых собственных вектора матрицы K

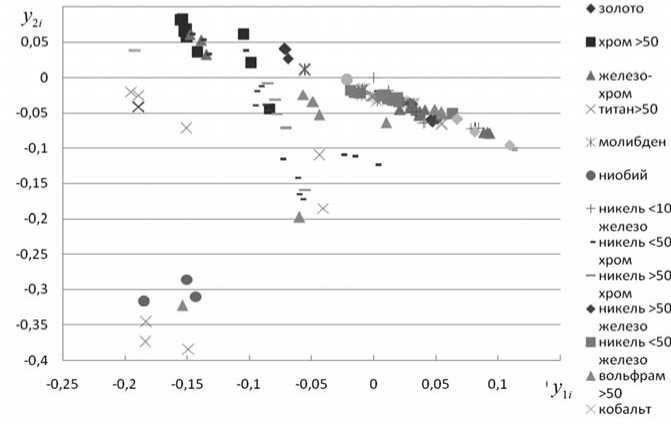
Рис. 3. Образы обучающей выборки в пространстве (у 1 , у ₂)

Для проверки эффективности методов автоматической кластеризации хронопотенциограмм к полученной выборке (рис. 3) применили метод к групповых средних [2,4] с критерием в форме отношения g= dID, среднего расстояния d между центрами кластеров к среднему внутриклассовому разбросу D. Получили оптимальное разбиение на 20 кластеров, что очень хорошо согласуется с реальным количеством распознаваемых сплавов, а именно 19 типов. Проверка показала, что правило распознавания kNN дает 57% правильных рас- познаваний даже в сочетании с лучшей в этом случае метрикой Журавлева:

k dim = 2 ^ где Iijr.

j =1

=

1,| y «

- Ут\ <  ^£ ;

_ 0,| У _у - У т\ ^ £ .

Для улучшения качества классификации был предложен 2-этапный подход: 1) разбиение выборки на классы по методу k групповых средних; 2) разделение полученных классов на фрагменты в соответствии с типом анодного поведения. Этот подход позволяет преодолеть проблему взаимопроникновения классов и дает возможность использовать в кластеризации метод линейных решающих функций. Фрагмент таких решающих функций показан на рис. 4.

ставила 95%, что доказывает его перспективность по отношению к рассматриваемой задаче.

Выводы:

• 1.    Собственные векторы ковариационной матрицы, полученной по выборке измерений на сплавах различной природы, представляют базовые типы зависимостей потенциала от времени. Им соответствуют активное растворение и пассивация.

• 2.    Проблема классификации по обучающей выборке с пересекающимися классами может быть решена использованием двухэтапного подхода.

• 3.    Полученный алгоритм идентификации типа сплава может быть использован в методиках электрохимического анализа конструкционных и специальных сплавов.