Математическое моделирование испаряемости нефти и нефтепродуктов при их аварийных разливах

• ·    невозможность расчета испарения нефтепродуктов (бензина, дизельного топлива, органических веществ, характерных для нефтехимии);

• ·    не учитывается скорость ветра над поверхностью разлива, приводящего к интенсификации испаряемости нефти и нефтепродуктов [4].

В [4].были получены эмпирические уравнения, учитывающие влияние скорости ветра над поверхностью разлива для ряда нефтепродуктов и нефтей.

Сопоставление опытных данных по испаряемостью Туймазинской и Арланской нефти при отсутствии ветровой нагрузки и нормативных материалов [3] свидетельствует о весьма приближенной оценке анализируемого процесса. Относительная погрешность расчета лежит в пределах 5-19% и определяется в первую очередь тем, что величина плотности нефти не является определяющим фактором испаряемости, так как различные нефти при одинаковой плотности могут иметь различный фракционный состав.

По сравнению с [3] более интересен предложенный в [5] эмпирический метод расчета испаряемости углеводородных систем, учитывающий состав и физико-химические свойства нефтепродукта и скорость ветра, в соответствии с которым испарение смеси углеводородов описывается уравнением:

N

G = Z ( 40 • 35 + 30 • 75 U ) * ^Ш 3 * P I * x I * M^ , (1) i = 1

где G - количество испаряющихся углеводородов, г/м^{2 .} ч;

N – число фракций в нефтепродукте,

U – скорость ветра на высоте 20 см над поверхностью разлива, м/с;

P I – давление насыщенных паров каждой фракции, Па;

x _I – мольная доля каждой фракции в испаряющейся углеводородной смеси;

M_I – молярная масса фракции, г/моль.

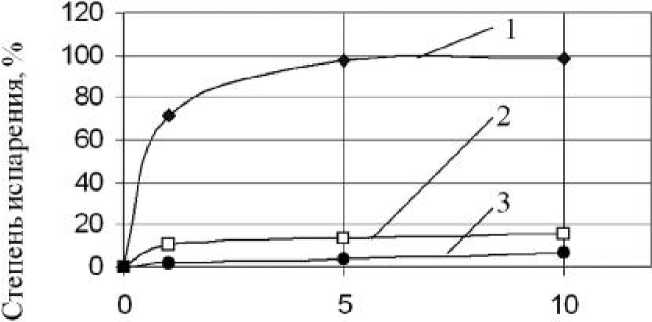
Время, часы

Рис. 1. Испарение во времени разлива автомобильного бензина (1), Туймазинской нефти (2) и дизельного топлива (3) при скорости ветра 0,4 м/с

Недостатком этого метода можно считать принятие постоянства испарения нефтепродукта во времени и отсутствие в [5] данных о погрешности расчета испаряемости.

Оценка приемлемости уравнения (1) как основы для расчета испарения нефтепродуктов выполнена нами в два этапа. На первом этапе выяснялась принципиальная применимость уравнения, на втором предполагалась модификация решения задачи на базе уравнения (1) с учетом постепенного испарения нефтепродукта с изменением его состава.

В связи с этим на первом этапе выполнен анализ применимости уравнения (1) сравнением результатов расчет испарения индивидуальных углеводородов по (1) и по методу Лыкова.

По формуле Лыкова [6] , расчет испарения индивидуальных углеводородов Q в г c поверхности F (м²) за время т (ч) рассчитывается на основе уравнения Дальтона как:

Q = A

MDRT

р _ р'

Ft ж ¹ ж

L

где A – коэффициент, зависящий от величины критерия Рейнольдса Re ;

D – коэффициент диффузии пара испаряющейся жидкости в воздух при температуре Т ( К), м²/ч;

R – универсальная газовая постоянная ( R =848/ М ), л^. атм /(К^. моль);

Р_Ж – давление насыщенного пара испаряющейся жидкости при температуре Т ( К), атм;

Р’_Ж – давление пара испаряющейся жидкости в воздухе, атм;

L – длина пути воздушного потока над поверхностью испарения, м.

При Re менее 20000

A = 0 . 5 Re ^{0 . 58} ,           (3)

при Re более 20000

A = 0 . 85 Re ^{0 . 76 .}           (4)

Сравнение расчетов по испарению индивидуальных углеводородов (н-пентана, н-гексана, н-октана и н-декана) по уравнениям (1) и (2) выполнялось для поверхности испарения 0.0067 м2 [5] при варьировании скорости ветра от 0 до 5 м/с и продолжительности испарения от 1 до 5 часов. Как следует из табл.1, при расчете испарения индивидуальных углеводородов уравнения (1) и (2) дают достаточно близкие результаты за исключением расчетов при скорости ветра, равной нулю, при которой уравнение (2) неприемлемо. Расхождения между двумя вариантами расчетов испарения нефтепродуктов не превышают 2-10 %отн., причем по мере увеличения продолжительности испарения расхождения существенно уменьшаются. Выполнена объективная оценка гипотезы о не значимости расхождений между двумя методами расчета при наличии ветра по статистическому критерию Стьюдента t. Согласно [7] , величина t рассчитывается как

t =

X 1 - X 2

^ 12

Z

Z

где X _I - средний результат расчета испарения углеводорода соответственно по уравнениям (1) и (2);

Z - число расчетных значений испарения углево ₂ дорода по каждому методу расчета;

Q i - дисперсия при расчете испарения углеводорода соответственно по уравнениям (1) и (2), рассчитываемая как

Таблица 1. Зависимость испарения углеводородов от скорости ветра

Скорость ветра, м/с	Время испарения, час	Испарение, г/ час
		н-пентан		н-гексан		н-октан		н-декан
		по [1]	по [2]	по [1]	по [2]	по [1]	по [2]	по [1]	по [2]
0	1	123	0	12	0	4	0	0.3	0
	3	370	0	36	0	11	0	1.1	0
	5	617	0	61	0	19	0	1.8	0
1	1	217	224	21	21	7	7	0.6	0.5
	3	653	672	64	64	20	22	1.9	2.0
	5	1088	1121	107	110	34	36	3.2	3.0
2	1	311	335	31	32	10	11	0.9	1.0
	3	935	1000	92	95	30	32	2.8	3.0
	5	1559	1674	153	159	48	54	4.6	5.0
3	1	406	434	40	40	13	14	1.2	1.0
	3	1218	1270	120	121	38	40	3.6	3.0
	5	2030	2116	200	201	63	68	6.0	6.0
4	1	500	501	49	48	15	16	1.4	1.5
	3	1500	1503	147	143	46	48	4.4	4.0
	5	2500	2504	246	238	77	80	7.4	7.0
5	1	594	570	58	54	18	19	1.7	1.5
	3	1782	1710	175	163	55	55	5.3	5.0
	5	2971	2850	292	272	91	92	8.8	9.0
Критерий Стьюдента при скорости ветра 1-5 м/с		0.05		0.07		0.02		0.19

a

I

ZZ

L x2j |L x.j j=iV j=i

Z - 1 Z (Z - 1)

где X _I,J – результат конкретного J -го расчета испарения углеводорода в г соответственно по уравнениям (1) и (2).

Расчетная величина критерия Стьюдента для всех исследованных углеводородов составляет 0.02-0.19 (табл. 1), она существенно ниже табличного значения критерия Стьюдента для 28 степеней свободы, равного 2.763 [7], что свидетельствует о не значимости расхождений между расчетами испарения углеводородов по уравнениям (1) и (2) при уровне вероятности ошибочности рассматриваемой гипотезы, равной 0.01.

На втором этапе исследования была разработана модель постепенного испарения нефтепродуктов при воздействии ветра при условии изменения состава испаряющейся во времени жидкости на основе уравнения (1), преобразованного в дифференциальную форму dg = L (40.35 + 30.75U)* 10'3 *PI*xI *-xM! * dr, i=1

где dg – количество испаряющихся углеводородов в г/м² за время d т

Решение задачи методом Рунге-Кутта первого порядка представляет собой интегрирование уравнения (7) во времени с шагами j и промежутками времени по шагам Дт с расчетом на каждом шаге ядра решения задачи в форме системы уравнений:

F = F ^х

^Fi,j - 1 F j - 1 ^xi,j - 1

N

^Fj - 1 = L ^Fi,j - 1 i = 1

g_ia = gi j - 1 + ( 4035 + 3075 U)* 10 ^{- 3} *P , ‘x ^ АД! , * Дт

N

Fj = Fj-1 -Lgi,j i=1

F_iH - ( 4035 + 3075 U)* 10 - ³ * P i *x i, _{j- 1} ^M i * Дт xi.i = n

L {F_{uj - 1} - ( 4035 + 3075 U)* 10 - ³ * P i *x i, _{j - 1} *^M i * Дт } i = 1

тj = тj-1 + Дт при следующих начальных условиях интегрирования:

то =0, Fo = Fha4 xi, о = xi,HA4 g, о =0.

В уравнениях (8) и (9):

F и F – соответственно количество неис-парившегос ⁱ я нефтепродукта и его конкретной фракции в разливе, г/м²;

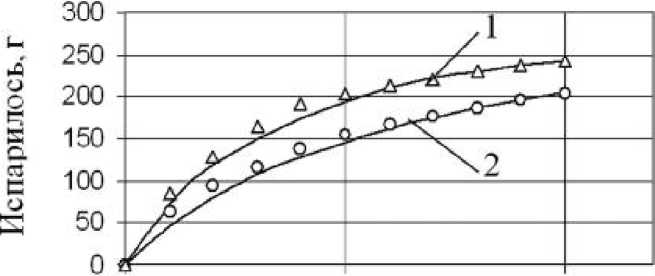
О               5               10