Математическое моделирование эксплуатационной скважины в процессе оптимизации нефтедобычи

Д.В. Коробатов, В.В. Запунный г. Челябинск, ЮУрГУ

* г. Мегион, НДК «Славнефть - Мегионнефтегаз»

Рассматриваются вопросы математического моделирования системы «нефтяной пласт - скважина - насос» на различных режимах её работы, включая режим оптимизации нефтедобычи. Большое внимание уделено технологии моделирования, определено место модели в процессе лабораторно-отработочных и эксплуатационных испытаний автоматизированной системы нефтедобычи, а также в реальных условиях эксплуатации.

Математическое описание процессов разработки нефтяных и нефтегазовых залежей имеет своей целью предсказание локальных и интегральных характеристик пластовой системы при различных условиях воздействия на нее, нахождение оптимальных режимов эксплуатации месторождений. Для математического моделирования процессов нефтедобычи используются различные подходы, основные результаты получены путем гидродинамического описания и анализа динамики пластовой системы с помощью дифференциальных уравнений, решения возникающих краевых задач. Такое описание опирается, обычно, на информацию, получаемую при выполнении поисковых и разведочных работ, бурении и эксплуатации скважин, геофизических исследованиях.

Уравнения, описывающие динамику пластовой системы, в общем случае являются многомерными нестационарными нелинейными уравнениями в частных производных. Возникающие краевые задачи, как правило, очень сложны, решать их аналитическими методами затруднительно, поэтому обычно прибегают к математическому моделированию.

Построение полноразмерной модели натыкается на недостаток достоверной информации о пластовой системе и происходящих в ней процессах для каждой конкретной добывающей скважины. Поэтому от модели потребуем отображения качественных закономерностей и таких количественных показателей, которые устойчивы к вариациям исходных данных. При этом будем исходить из идеи «разумной» точности моделирования. Возможную потерю точности скомпенсируем включением в модель адаптационных механизмов, обеспечивающих гибкую настройку и перенастройку модели под конкретный рабочий режим скважины и изменившийся характер нефтедобычи.

К математической модели системы «нефтяной пласт - скважина - насос» помимо отражения реальных физических процессов, происходящих в нефтяном пласте и скважине при добыче, добав ляются технологические требования, связанные с технологией математического моделирования. Математическая модель должна просто настраиваться и перенастраиваться при изменившихся условиях добычи, параметрах пласта и скважины, должна быть «обозримой» и удобной в работе, легко сопрягаться с другими элементами (блоками) технологического комплекса.

В нашем случае одной из основных целей математического моделирования была отработка аппаратной и программной частей автоматизированной системы управления станком-качалкой (АСУСК) на всех рабочих режимах её работы, включая режим оптимизации нефтедобычи в процессе реальной эксплуатации скважины. Поэтому от математической модели системы потребуем совместимость с АСУ СК (модель становится частью АСУ СК) как при проведении лабораторноотработочных, так и эксплуатационных испытаний автоматизированной системы. Во втором случае используется мобильный вариант модели, который может быть оперативно подключен к АСУ СК для настройки программного комплекса системы. Таким образом, технологический комплекс моделирования и оптимизации нефтедобычи превращается в полунатурный комплекс. Такой подход ведёт к существенной экономии средств, так как большой комплекс задач, таких как отладка аппаратной части, отработка алгоритмической и программной частей АСУ СК, перенастройка автоматизированной системы при изменении условий добычи, проводится в лабораторных условиях без выезда на места нефтедобычи. Постоянно действующая модель системы в условиях неполноты, неточности исходной геологической и промысловой информации, кроме того, становится важнейшим инструментом прогноза и оценки эффективности методов повышения нефтедобычи.

Структура математической модели системы «нефтяной пласт - скважина - насос» представлена на рис. 1. Здесь приняты следующие обозначе- ния: п - число двойных ходов плунжера насоса в минуту, DH - производительность насоса, D - дебит скважины, Рпн - давление на приёме насоса.

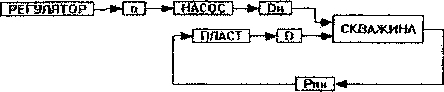
Рис. 1. Структурная схема математической модели системы «нефтяной пласт - скважина - насос»

Модель насоса включает его геометрические параметры, коэффициент подачи насоса и параметры настройки производительности насоса:

°н = 8таип, где 5^ = — с/ш - сечение плунжера насоса (диа метр плунжера выбирается в диапазоне 28-120 мм); / - длина хода штока (0,5-6 м); J - коэффициент подачи (0,7-0,8). Уравнение насоса может быть записано более компактно:

DK=KHn.

Здесь К_н - «коэффициент насоса». Он подбирается исходя из условия обеспечения необходимой пиковой производительности насоса. Регулировка этого коэффициента позволяет менять производительность насоса в широких пределах. При этом необходимо учитывать, что увеличение п выше некоторого уровня снижает коэффициент подачи насоса, так как при быстром качании не успевает заполняться цилиндр насоса, особенно на вязких нефтях.

Модель скважины отражает её геометрию, процессы наполнения и опорожнения за счёт взаимодействия скважины с пластом и насосом:

V^=^D^-D_B^dt ₊ V_Q-, h = V/S; P_m=h_Y; о

^'дин — '^сп — ^> ^заб ~ (^заб — -^сп )У + ^пн > где Ко и К- начальный и текущий объём флюида в рабочей зоне скважины (от приёма насоса до устья скважины); h - высота столба жидкости в рабочей зоне скважины; S = ?г^ -г^ - площадь сечения затрубного пространства скважины (гс и гтр -радиусы скважины и трубы, соответственно); Нзаб - глубина забоя; Ясп - глубина спуска насоса; Н№Н - динамический уровень нефти в сква жине; 7(аб - забойное давление, у - удельный вес флюида. Выходными координатами модели скважины являются давление на приёме насоса и динамический уровень флюида в скважине. ■

Наиболее сложной является модель пласта, отражающая его фильтрационно-емкостные параметры. Исходной информацией для моделирования пласта являются величины пластового давле- ния, глубина забоя, глубина спуска насоса, плотность флюида, продуктивность пласта, его коллекторские свойства. Коэффициент продуктивности пласта является сложной функцией депрессии на пласт и других факторов:

= ^пл -^аб>

Knp^ = KY-K2ZXP, где Р^ - пластовое давление, \Р - депрессия на пласт, Кпр - коэффициент продуктивности пласта; Кх и К2 - комплексные параметры пласта, характеризующие его добывные возможности. Расчёт этих параметров проведём по следующим соотношениям:

„ ~ Dq max        Dq max

AP 2 AP2 штах       ^max где DOmax - максимальная производительность скважины; A/^ - депрессия на пласт, при которой достигается максимальная производительность скважины. Оценочные значения последних величин (О0тах, А/^ ) определяются при гидро динамических расчётах. Здесь Do - установившееся значение производительности скважины, определяется по следующему соотношению:

П0=Хпр(ДР)-АР.

«Динамика» пласта описывается следующим уравнением:

Тс—+D = Dq, с dt 0

где Т_с - постоянная времени скважины (также комплексный параметр модели пласта, зависящий от множества факторов). Постоянная времени может быть оценена исходя из средней продуктивности пласта:

Т = 5

где К*_р - коэффициент «средней» продуктивности пласта. Целью моделирования пласта является определение критических дебитов (предотвращение конусообразования газа и воды) и эффективных максимальных дебитов (оптимальная работа скважины).

В модель пласта включены механизмы временного дрейфа (изменения) параметров пласта, подверженных сезонным колебаниям и изменениям, связанным с характером нефтедобычи. На рис. 2 приведён пример комбинированного (горизонтального и вертикального) дрейфа параметров. В случае необходимости параметры дрейфа могут уточняться в процессе реальной эксплуатации АСУ СК.

Характеристики нефтяного пласта соответствуют Аганскому месторождению компании «Славнефтегаз», г. Мегион:

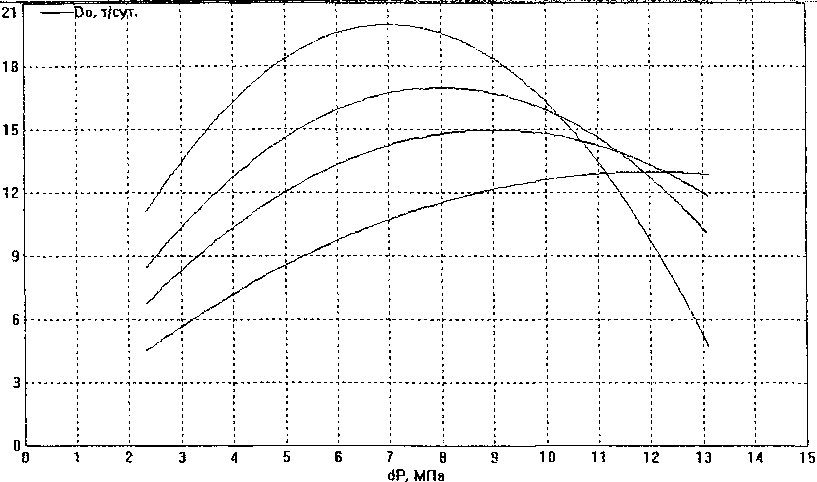
Рис. 2. Изменение производительности пласта в процессе длительной эксплуатации скважины (зависимость стационарной производительности скважины от депрессии на пласт)

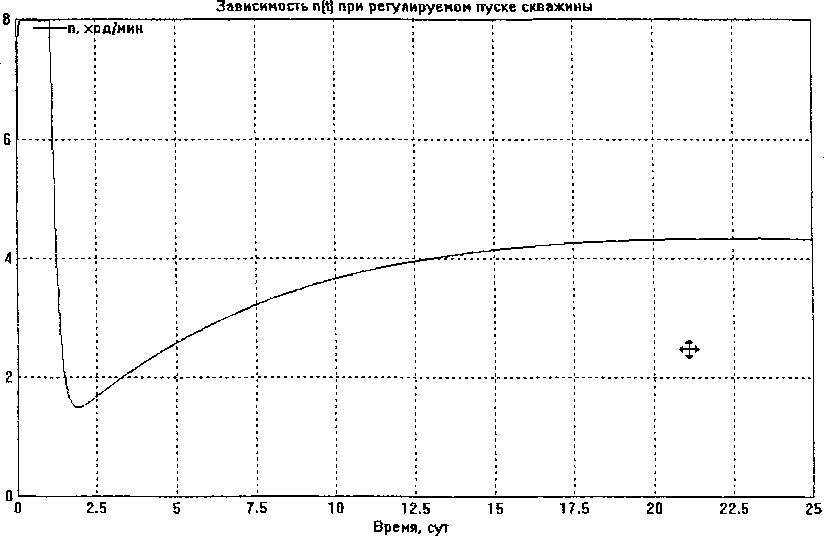
Рис. 3. График регулируемого пуска скважины и её выхода на режим стационарной нефтедобычи

• •    пластовое давление 15-28 МПа;

• •    глубина забоя 1700-2600 м;

• •    глубина спуска насоса 1200-2000 м;

• •    забойное давление 6,5-26 МПа;

• •    давление на приёме насоса 2-17 МПа;

• •    депрессия на пласт 2-21,5 МПа;

• •    удельный вес флюида 850-900 кг/м³;

• •    число двойных ходов плунжера в минуту 1-20.

Математическое моделирование системы «нефтяной пласт - скважина - насос» в режимах опорожнения скважины, восстановления давления,

«запуске» скважины и выходе её на режим добычи подтверждают адекватность динамической модели системы реальным процессам нефтедобычи на Аганском месторождении. На следующем рис. 3 приведён график пуска скважины и выхода её на стационарный режим нефтедобычи. На рис. 4 представлен режим восстановления давления.

На разработанной модели системы проведена отработка алгоритмов оптимизации нефтедобычи. Ниже приведено (рис. 5) семейство фазовых кривых «дебит - давление на приёме насоса», демон- стрирующее поисковый характер оптимизации добычи. Разные кривые соответствуют различным условиям исходной добычи скважины (до оптимизации) во всём рабочем диапазоне давлений на приёме насоса. Система управления обеспечивает устойчивую нефтедобычу на всех режимах работы и выводит скважину на максимально возможную нефтедобычу (для данного случая пиковая производительность скважины соответствует 20 т/сут.). Проведено математическое моделирование систе-

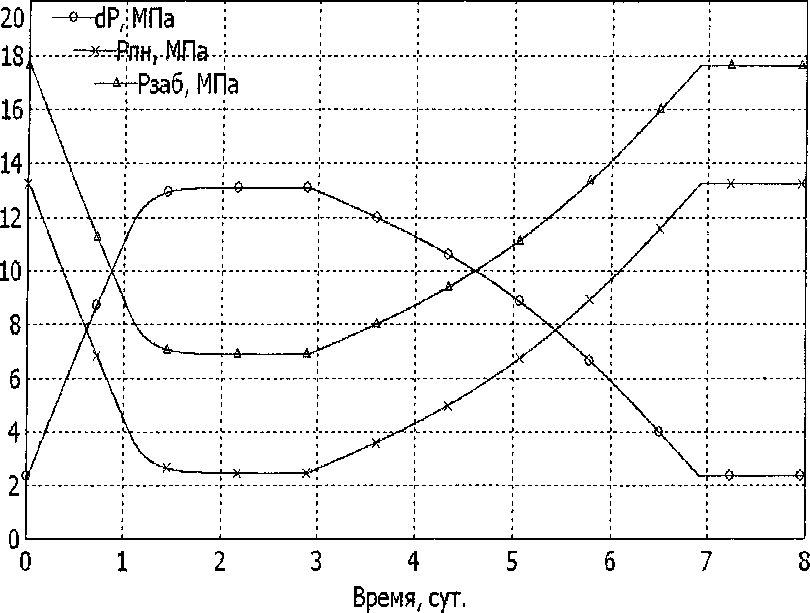
Рис. 4. Г рафик заполнения скважины (кривая восстановления давления)

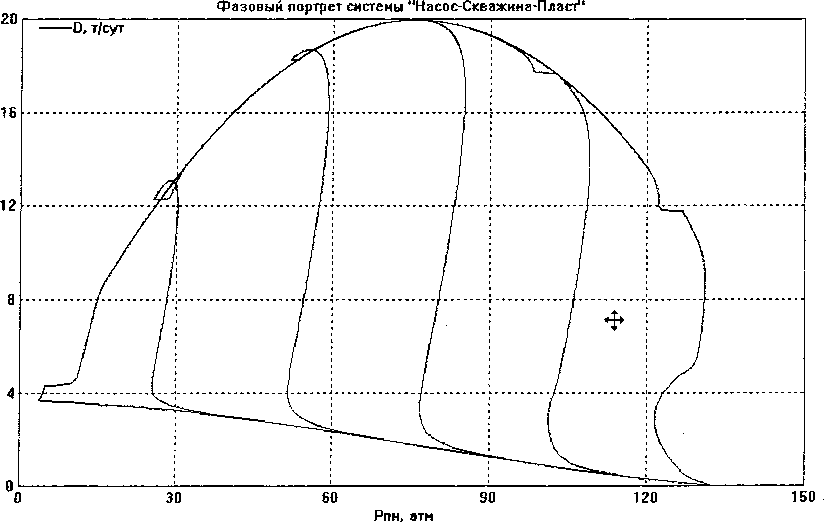
Рис. 5. Зависимость дебита скважины от давления на приёме насоса в режиме запуска скважины, выхода её на стационарный режим добычи и оптимизации нефтедобычи для различных условий добычи

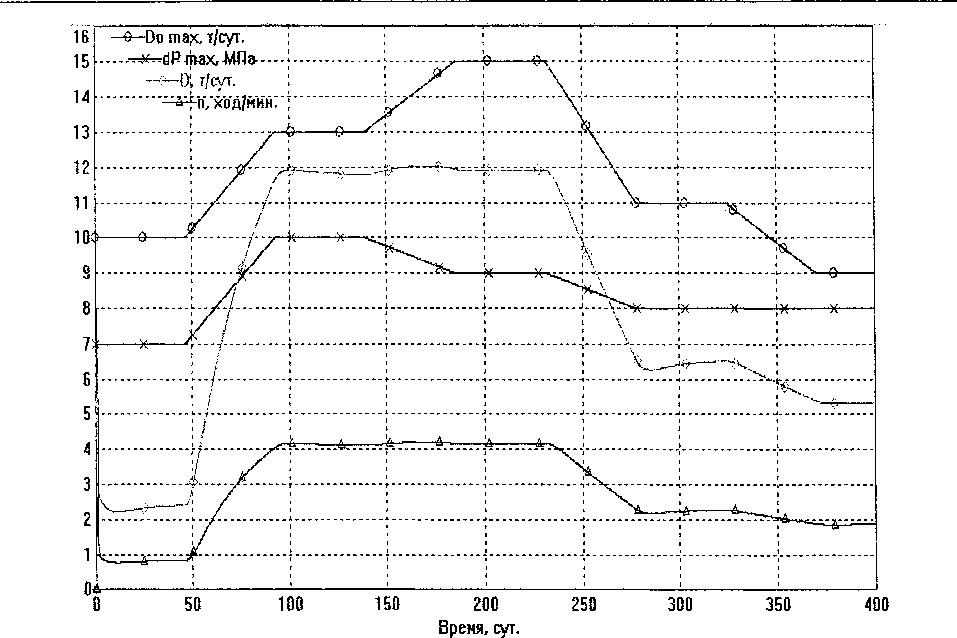
Рис. 6. Моделирование системы «нефтяной пласт - скважина - насос» в процессе длительной эксплуатации скважины (более года) в условиях изменяющейся продуктивности пласта

мы в условиях дрейфа параметров пласта. Разработанные алгоритмы управления и оптимизации нефтедобычи продемонстрировали и здесь свою эффективность (рис. 6).

В заключение хотелось бы отметить, что представленная концепция математического моделирования работы одиночной эксплуатационной скважины в режиме нефтедобычи нашла своё подтверждение на практике. Разработанная математическая модель системы «нефтяной пласт - скважина - насос» широко использовалась для отладки аппаратной и программной частей АСУ СК. С по мощью математической модели отработаны алгоритмы управления станком-качалкой, включая режим оптимизации нефтедобычи. В настоящее время АСУ СК успешно апробирована и находится в стадии внедрения на предприятии заказчика.