Математическое моделирование электро-магнитных процессов в датчиках тока для систем защиты электрооборудования

Введение. В качестве первичных датчиков современных систем токовой защиты электрооборудования используются промышленные трансформаторы тока и датчики Холла, стоимость которых сравнительно высока, а применимость ограничена. Поэтому перспективны альтернативные конструкции, характеризующиеся низкой стоимостью и улучшенными эксплуатационными показателями. Наиболее привлекательным представляется датчик тока на основе охватывающего проводник проводящего ферромагнитного кольца, конструкция которого приведена на рисунке.

Целью данной работы является математическое моделирование электромагнитного процесса в системе «проводник с синусоидальным током, охваченный ферромагнитным проводящим кольцом».

Решение задачи расчета электромагнитного поля в системе с линейным проводником, по которому протекает синусоидальный ток, охваченный ферромагнитным проводящим кольцом, позволяет определить выходное напряжение на сигнальной обмотке кольца (см. рисунок). Поскольку величина тока достаточно мала, т.е. электромагнитный процесс протекает на начальном участке кривой намагничивания, задачу можно считать линейной [1].

Проводящее ферромагнитное кольцо: И-) - первичная обмотка (шина с синусоидальным током); И-? - вторичная или выходная обмотка; м_с - выходной сигнал; 1 - железный (стальной) короткий отрезок трубы или кольцо, выточенное из прутка обыкновенной стали широкого применения

Установим связь между выходным напряжением сигнальной обмотки н_с и током i.

При данной постановке задачи магнитная проницаемость сердечника ц— постоянная величина, не зависящая отН, причем ц>>1. Сердечник обладает электропроводностью у (для стали у»Г107 Ом"1^"1).

Используем цилиндрическую систему координат для случая, когда синусоидально изменяющийся во времени ток направлен по оси Z, а составляющие векторов Е и Н электромагнитного поля внутри железного сердечника не зависят от а и Z цилиндрической системы координат.

Уравнение электромагнитного поля для проводящей среды имеет, как известно, вид [1]:

rotH = 5;

roti) = -усоуцН, где 5 - вектор плотности тока в проводящей среде.

Из (1) и (2) получим rotrotS = -усоуцЗ.

Преобразуя левую часть, получаем grad divS - v28 = -ушуцЗ.

С учетом установившегося режима (div8 = 0)

V28 = усоуцЗ.

Раскрывая V25 в цилиндрической системе координат и учитывая, что 5 от а и Z не зависит, придём к частному случаю уравнения Бесселя:

d²t> , 1 db а _п ------Т "I---77 7 + О — О, d{qry qr d(qr)

Решение уравнения (3) можно записать как

5 = M_YJ₀(qr) +M₂N₀(qr), где Mi и М^ -постоянные интегрирования; Jody) -функция Бесселя нулевого порядка первого рода; ^о (?^г) - функция Бесселя нулевого порядка второго рода.

Функция ^о (?г) обращается в бесконечность при г = 0.

Ясно, что 5 не может обращаться в бесконечность, поэтому в рассматриваемом случае М2 должно быть равно нулю, следовательно t = MYJ0(qry

На основании (2), с учетом раскрытия rotS в цилиндрической системе координат и зависимости 5 только от координаты Z получаем выражение для вектора напряженности магнитного поля в железном сердечнике:

— ^VMiJ^qr^A = —J^qr), q dr             q

где J^qr) -функция Бесселя первого рода первого порядка.

Определим постоянную интегрирования М_х , с этой целью по закону полного тока найдем значение Н_т на внутренней поверхности трубы:

H (г = я) = т 11 тМ         о ■> где Нт и 1т - комплексные амплитудные значения напряженности магнитного поля и контролируемого тока.

Приравняем значение Н _т (г - д) _к правой части равенства (4):

1_т М_л , , _Л> qlm = —JAqrA, тогда Мг = ---——-.

2лд q ^1/1              27tr_xJ_x(qr_x)

После подстановки (5) в (4) получаем:

₉ Л V itor),

Зависимость В_т - \\Н_т для железного сердечника считаем линейной, а уравнение магнитного потока, который пересекает витки сигнальной обмотки, с учетом (6) запишем в виде

Ф„ = /г f vxH_mdr =           f Jx^dr.

Комплексное амплитудное значение выходного напряжения сигнальной обмотки выразим как т J               2KrxJx(qrx) ’

Для определения выходного сигнала рассматриваемого датчика тока по формуле (7) необходимо вычислить интегральное значение функции Бесселя первого рода первого порядка от комплексного аргумента:

где А - глубина проникновения поля в ферромагнитную среду, А = ^/соуц.

Чтобы вычислить функцию Бесселя от этого аргумента, воспользуемся ее интегральным представлением [2]:

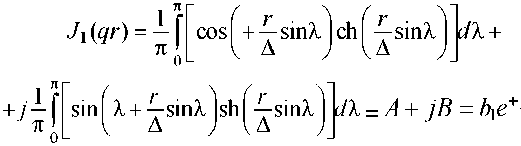
где А - реальная часть комплексного числа Л(^^г); В - мнимая часть комплексного числа

ЬХ=^А2+В2 ;

Pi = arctgS / А.

При допустимых заданных значениях ®, у, ц А, и Pi зависят от геометрических размеров кольца и глубины проникновения А.

После подстановки (8) в (7) определяем:

. _ jtowchyilm т lTO\Jx(qr^

Г1

п

п

Амплитудное значение выходного сигнала при указанных допущениях пропорционально амплитудному значению тока. Кроме того, следует выяснить, какой фазовый сдвиг имеет выходной сигнал относительно первичного тока V . Для этого необходимо определить Pi и аргумент комплексного числа Л(дгА, учитывая, что j = V°°

Расчет U_{m П}о формуле (9) проведен для следующих параметров устройства:

П = 17 мм; h = 17 мм; У =Г10⁷ Ом^-1‘м^-1;    1_т= 30лр2А;

г₂ = 22 мм; ц = 1ООц_о; /=5ОГц; w_c = 220.

С такими конструктивными параметрами был изготовлен экспериментальный образец.

В результате расчета выходного сигнала с использованием программы MathCad по формуле (9) для приведенных выше данных получены зависимости:

J₁(^r₁) = ^ + jB = b_xe^ = -179,1 + /140 = 227, бе⁷¹²⁰”

I" Adr + 7 j Bdr = 0,84 e^jX9TB.

Если изменить полярность выходного сигнала на 180° обратным включением сигнальной обмотки, то выходное напряжение запишем как U_m = 0,84е⁷¹⁷ В, т.е. несколько опережающее по фазе ток первичной обмотки.

Результаты проведенных расчетов показывают, что сдвиг по фазе между выходными сигналами напряжения и тока источника имеет величину порядка 17°.

Выводы. Разработанная авторами методика расчета электромагнитных параметров перспективного датчика тока на основе охватывающего проводник ферромагнитного кольца позволяет существенно облегчить этапы проектирования и доводки подобных устройств. Ввиду низкой стоимости и хороших эксплуатационных показателей рассмотренная конструкция представляется выгодной альтернативой современным датчикам на основе токовых трансформаторов и чувствительных элементов Холла.