Математическое моделирование как способ управления затратами на предприятии

На современном этапе развития российской экономики для многих предприятий проблема снижения затрат является одной из ключевых.

В нынешних непростых экономических условиях нашей страны управление затратами рассматривается как средство получения предприятием высокого экономического результата, поскольку в общем виде он определяется разностью дохода от продажи продукции и затрат на ее производство и сбыт. Производственные затраты занимают основное место в структуре затрат предприятий, концентрируя в себе результаты всех направлений их деятельности.

Классические проблемы управления производственными затратами затрагивают решение вопросов планирования, учета, анализа, контроля затрат, снижения себестоимости продукции. Вместе с тем, становление рыночных отношений требует изменения взглядов на управление производственными затратами с учетом особенностей переходного к рыночной экономике периода, значительных новаций, происходящих в технологии производства, в потребительских предпочтениях, в конкурентной среде.

Термин "управление затратами" как самостоятельное понятие используется в нашей стране сравнительно недавно. Это объясняется тем, что при жесткой регламентации хозяйственной жизни в условиях централизованно управляемой экономики затратного и государственного ценообразования интерес к информации о действительных издержках носил достаточно условный характер, да и сама информация в условиях государственной собственности не могла иметь подлинной значимости и полезности. Проблемами ценообразования продукции занимались государственные структуры, сами цены устанавливались исходя из совокупных затрат на производство и реализацию продукции. Поэтому у руководителей предприятий не было реальных стимулов к снижению издержек через управление ими. К сожалению, данная тенденция сохраняется и по сей день, когда рентабельность работы предприятия обеспечивается за счет достаточно высоких отпускных цен, а не за счет экономии в расходовании производственных ресурсов. Однако в современных условиях цену диктуют законы спроса и предложения, таким образом возникает необходимость достижения такого уровня затрат на производство и реализацию продукции, который был бы ниже возможной рыночной цены, обеспечивая необходимый уровень рентабельности.

Таким образом, уже сейчас следует четко определить не только роль и функции управления затратами, но и весь инструментарий приемов и методов, которые позволяют выполнять эти функции наиболее эффективным образом.

Среди многочисленных методов управления затратами существуют экономико-математические методы (производственные функции, моделирование, линейное программирование). Экономико-математические методы представляют собой сочетание экономических, математических и кибернетических методов. Центральным понятием методов этой группы является оптимизация, т. е. процесс нахождения наилучшего варианта из множества возможных с учетом принятого критерия.[4]

Одной из типичных задач линейного программирования является так называемая транспортная задача. Она возникает при планировании наиболее рациональных перевозок грузов, а также при организации и планировании производства.

Если рассматривать, например, оптимизацию перевозок груза или товаров, то наилучшим приемом будет транспортная задача. С её помощью мы можем составить план перевозок, при котором общая стоимость доставки продукции будет наименьшей.

Допустим, нас интересует оптимизация логистических затрат - такие затраты есть практически у любого торгового или производственного предприятия. Логика решения проблемы оптимизации транспортных затрат вполне применима и для других, более существенных статей.

Предположим, что предприятие имеет два складских помещения, откуда товар поступает в пять магазинов, разбросанных по всему городу. Магазины в состоянии реализовать определенное количество товара. Каждый из складов имеет ограниченную вместимость. Оптимизация управления затратами подразумевает, что следует определиться, с какого склада в какие магазины нужно доставлять товар, чтобы минимизировать общие транспортные расходы. Другими словами, определить оптимальные маршруты и объемы поставок. Конечно, мы несколько упрощаем условия, но если речь будет идти не о нескольких магазинах, расположенных в одном городе, а о сотнях или тысячах торговых точках по всей стране, схема решения будет основана на тех же принципах. Разберем их подробнее.

Оптимизация затрат предприятия: поиск решения

В математике задачи выбора оптимального маршрута по нескольким точкам относят к классу так называемых транспортных задач (Vehicle Routing Problems, VRP). И конечно же, давно разработаны способы их решения. [1] Excel предоставляет пользователю один из них – надстройка «Поиск решения» (Solver) в меню «Сервис» (Tools). Перед началом оптимизации затрат предприятия необходимо будет составить несложную таблицу в Excel – нашу математическую модель, описывающую ситуацию (см. рис. 1).

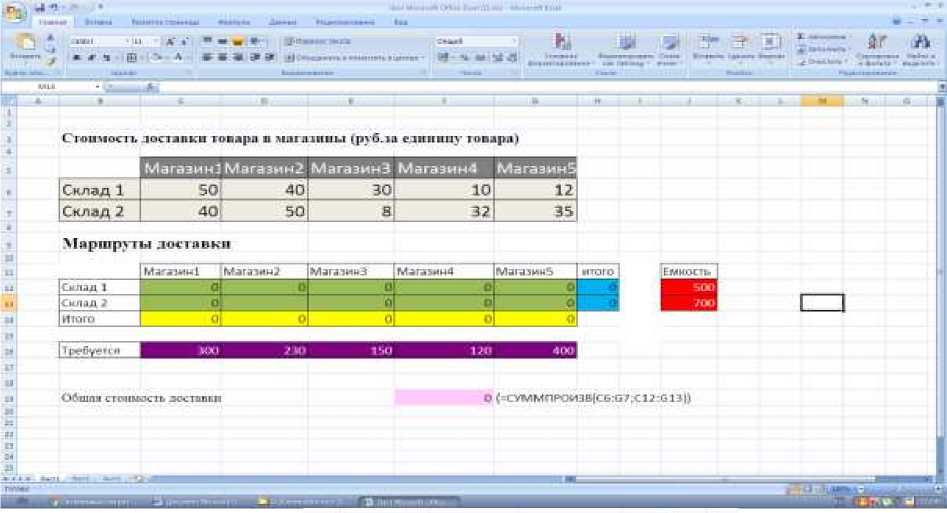
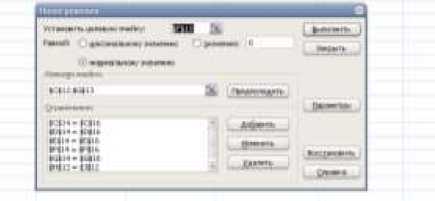
Рисунок 1. Исходные данные для оптимизации транспортных затрат

Подразумевается, что:

– серая таблица (B3:G5) описывает стоимость доставки единицы товара от каждого склада до магазина;

– лиловые ячейки (C14:G14) описывают необходимое для магазинов количество товаров на реализацию;

– красные ячейки (J10:J11) отображают емкость каждого склада – предельное количество товара, которое склад может вместить;

– желтые (C12:G12) и синие (H10:H11) ячейки – соответственно суммы по строке и столбцу для зеленых ячеек;

– общая стоимость доставки (E17) вычисляется как сумма произведений количества товаров на соответствующие им стоимости доставки.

Таким образом, наша задача сводится к подбору оптимальных значений поставок в магазины, которые будут отражены в зеленых ячейках.

Причем так, чтобы общая сумма по строке (синие ячейки) не превышала вместимости склада (красные ячейки) и при этом каждый магазин получил необходимое ему количество товаров на реализацию (сумма по каждому магазину в желтых ячейках должна быть как можно ближе к требованиям – лиловым ячейкам).

Настройки оптимизации затрат предприятия

Чтобы выполнить оптимизацию затрат, нужно открыть меню «Сервис»

(Tools) и выбрать команду «Поиск решения» (Solver). После этого откроется одноименное диалоговое окно, в котором потребуется задать следующие настройки:

• •    «целевая ячейка» (Target cell) – здесь необходимо указать конечную главную цель нашей оптимизации, то есть розовую ячейку с общей стоимостью доставки (E17). Целевую ячейку можно минимизировать (если это расходы, как в нашем случае), максимизировать (если это, например, прибыль) или попытаться привести к заданной константе;

• •    «изменяемые ячейки» (By changing cells) – здесь нужно задать зеленые ячейки (C10:G11), варьируя значения которых мы хотим добиться требуемого результата – минимальных затрат на доставку;

• •    «ограничения» (Subject to the Constraints) – список ограничений, которые надо учитывать при проведении оптимизации. В нашем случае это ограничения на вместимость складов и потребности магазинов. Для добавления ограничений в список нужно нажать кнопку «Добавить» (Add) и ввести условие в появившееся окно. Кроме очевидных ограничений, связанных с физическими факторами (вместимость складов и средств перевозки, ограничения бюджета и сроков и т. д.), иногда приходится добавлять ограничения «специально для Excel». Например, нужно будет добавить условие, что объем перевозимого товара (зеленые ячейки) не может быть отрицательным (то есть больше или равно нулю). Для человека такое само собой очевидно, но для компьютера это надо прописать явным образом.

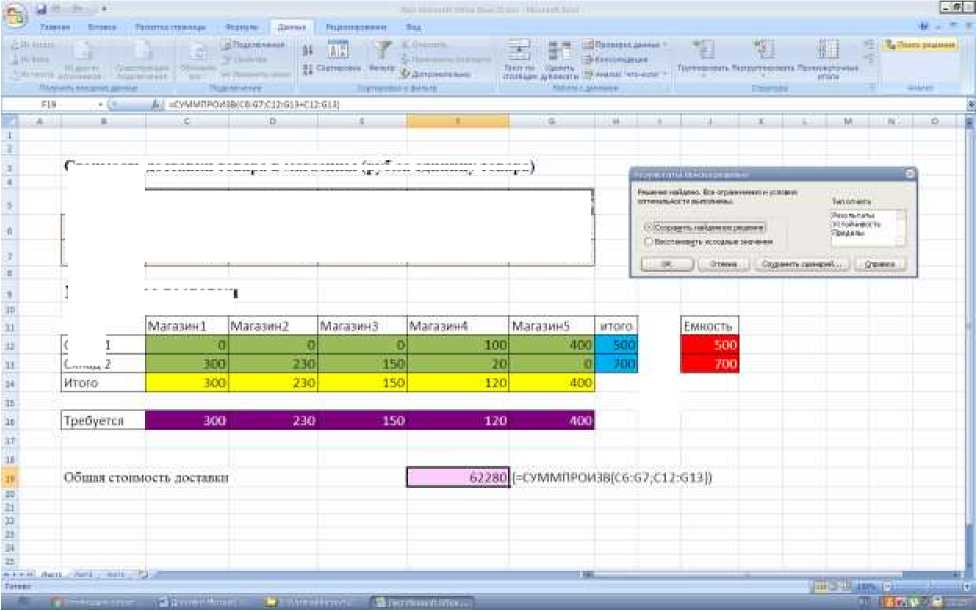
Теперь, когда данные для расчета введены, останется нажать кнопку «Выполнить» (Solve) - начнется оптимизация затрат предприятия. В тяжелых случаях с большим количеством изменяемых ячеек и ограничений нахождение решения может занять продолжительное время, но описываемая задача для Excel проблемы не составит – через пару мгновений результаты будут готовы (см. рис. 2).

	Магазин]	Магээмн2	МагэзинЗ	МагазинД	Магазин 5
Склад 1	50	40	30	10	12
Склад 2	40	50	8	32	35

Млршрчы доставки

Склад 1

Склад 2

Рисунок 2. Результаты оптимизации транспортных затрат Универсальная оптимизация затрат предприятия

Описанный пример, конечно, предельно прост, но может быть легко масштабирован под решение гораздо более сложных нелинейных задач. Логика, в основе которой поиск решения с учетом существующих ограничений, вполне подходит, например, для оптимизации:

• •    распределения финансовых средств по статьям расходов в бизнес-плане или бюджете проекта компании. Ограничениями в данном случае будут являться объемы финансирования и сроки выполнения проекта, а целью оптимизирования - максимизация прибыли и минимизация расходов на проект;

• •    расписания сотрудников с целью минимизации фонда заработной платы предприятия. Ограничениями в этом случае будут пожелания каждого сотрудника по графику занятости и требования штатного расписания;

• •    инвестиционных вложений - необходимость грамотно распределить средства между несколькими банками, ценными бумагами или акциями предприятий с целью опять же максимизации прибыли или (если это более важно) минимизации рисков.

В данной статье рассмотрена простейшая задача, цель статьи — побудить экономистов использовать в расчетах инструмент Excel «Поиск решений», который удобен и прост в применении. Освоив и поняв данный инструмент, можно будет переходить к более сложным задачам.