Математическое моделирование кавитационных процессов при кондиционировании промышленных сточных вод

Одними из факторов эффективной безреагентной очистки промышленных сточных вод являются эффекты гидротермодинамического кавитационного воздействия, возникающего в суперкавитационном реакторе (СК-реакторе). В связи с этим требуется разработать комплексную математическую модель возникновения эффектов кавитации с параметрированием показателей возникающей при этом энергии и физико-химических процессов модифицирования загрязняющих веществ. Динамику кавитационных микропузырьков представляют условно как два взаимосвязанных процесса – рост и последующее схлопывание. Так как процесс гид-ротермодинамической кавитации происходит в водной среде, то при возникновении и динамике каверны формируются гидродинамические течения, а при схлопывании выделяется энергия, способствующая как модифицированию молекул воды, так и реакционному цепному преобразованию химических примесей.

Целью исследований является математическое моделирование кавитационного процесса, происходящего на границах раздела фаз в исследуемой среде и подбор оптимальных режимов кавитационной обработки сточной воды с целью ее эффективной очистки.

Изменение физико-механических свойств жидкости при гидротермодинамическом кавитационном воздействии основано на высокой концентрации (кумуляции) энергии в очень небольшом объеме газообразной и жидкой среды с последующим ее высвобождением в критически малом временном периоде.

Физические характеристики жидкости оказывают различное влияние на интенсивность кавитационного воздействия, увеличивая или уменьшая скорость кумулятивных струек вблизи твердых границ потока. Особенно сильно это влияние сказывается на последнем этапе схлопывания пузырьков, когда их размеры очень малы. Увеличение вязкости и плотности снижает интенсивность кавитационного воздействия; силы поверхностного натяжения ускоряют коллапс пузырьков; наличие растворенных и нерастворенных газов в жидкости замедляет этот процесс, демпфируя соударение стенок пузырька. Поэтому дегазация жидкости служит одним из способов интенсификации кавитационного воздействия.

Изменение условий проведения технологических процессов также может существенно влиять на интенсивность кавитационного воздействия, а следовательно, и на скорость протекания соответствующего процесса. Например, снижение температуры и давления насыщенных паров повышает интенсивность кавитационного воздействия. Повышение давления увеличивает скорость кумулятивной струйки при схлопывании пузырька, однако при значительном повышении статического давления трудно получить режимы развитой кавитации.

Время кавитационной обработки также неоднозначно влияет на конечный результат. Не всегда увеличение времени обработки ведет к увеличению технологического эффекта. Поэтому, применяя гидродинамическую кавитацию, необходимо учитывать не только физические свойства жидкостей, но и условия проведения конкретного технологического процесса: давление, температуру, длительность обработки, степень турбулентности потоков, наличие твердых частиц и т. д.

Влияние сил вязкости и сил поверхностного натяжения на скорость схлопывания кавитационных пузырьков при условии сферического схлопывания возможно оценить интегрированием уравнения движения границы пузырька

2 2 lR We

RR +— R +----1---+1 — 0,

3 Re R η где R – максимальный начальный радиус кавитационного пузырька перед схлопыванием; t – время; ρ – плотность жидкости; R – критический радиус; R – текущий радиус, т.е. расстояние в тепловом пограничном слое (примыкающем к поверхности раздела фаз), отсчитываемое

R

от центра пузыря; P 0 = P ∞ – P d – разность давлений на бесконечности и насыщенных паров ;

R P ρ                       2σ

Re = — --- число Рейнольдса; We =--число Вебера ( ц - коэффициент динамической

4μ                       P0R вязкости; σ – коэффициент поверхностного натяжения). В частном случае для воды эти параме- гн тры равны: р = Г10-3 Па^с; р = 1—3; Pd = 2.4'104 Па; о = 7,5 -10 2 — при Т = 20 °С.

см ³                           м

Если пренебречь вязкостью Re → ∞, но учесть действие сил поверхностного натяжения, то уравнение (1) удается проинтегрировать. На конечной стадии смыкания пузырька, которая в основном определяет технологические результаты, скорость смыкания при R <<  1

■         2 J 3     1

R ≅ R ^{- 3} 1 + We .

R → 0

V 3 I 2     )

Отсюда силы пове хностного натяжения величивают ско ость движения границы пу-

'      3        Л ¹/²

1 + ^ We I раза.

зырька R на последних этапах его схлопывания в

Для о енки влияния сил вязкости можно по ставить асимптотическое значение скорости

³ D-3 замыкания для идеальной жидкости R = J— ( R

1) , т. е. незначительной вязкости жидкости.

Проинтегрировав (2), получим уравнение движения границы пузырька

/

R =

2/ з x 3

-(R - 1) 1 + 3We ■

3'          ) l -

1 - R2 -V6 1 - R1/2) ■

1 - R³    Re  1 - R ³ J

.

Этот результат показывает, что влияние вязкости приводит к уменьшению скорости смыкания. Существуют условия, при которых влияние вязкости и сил поверхностного натяжения будет взаимно компенсироваться. На последних этапах смыкания при R → 0 скорость смыкания

/2 Г7 3 "г ГТ R r _ 0 =_A 2 R -| 1 + -We - 2V6 • —I . \ 3 V 2           Re )

Условие компенсирования указанных сил выполняется при соблюдении равенства и не зависит от начального размера пузырька

We =

4 2 ₃ Re ^.

Для жидкости с заданными физическими свойствами равенство «отрицательных» сил вязкости и «положительных» сил поверхностного натяжения наступает при вполне определенном значении внешнего давления P 0 , величину которого легко получить из (5):

P = 2,34 - 10 ^{- 2 p о}

Например, для воды P ₀ ≅ 1,3 ⋅ 10⁵ Па при Т = 20 ºС.

Таким образом, на последних стадиях схлопывания кавитационных пузырьков в воде силы поверхностного натяжения будут уравновешиваться силами вязкости при давлении в жидкости P _∞ = 1,54 × 10⁵ Па. Необходимо отметить, что область решения (3) ограничена условием

Re >  2V6/ ( 1 + 3 J We.                                           (7)

Очевидно, что влияние сил поверхностного натяжения и вязкости будет малым при выполнении неравенства

3_We - 2^6 <<  1.                                             (8)

2 Re

Так, для воды в диапазоне изменения внешнего давления 10⁶ > P 0 > 2·10⁵ Па скорость замыкания пузырька с радиусом R_max = 1 мкм уменьшается из-за действия сил вязкости всего на 20 %.

При давлении P ₀ большем, чем (6), на последних этапах преобладают силы вязкости, уменьшающие скорость смыкания, при меньшем – силы поверхностного натяжения, увеличивающие скорость схлопывания. Однако, как показывают вычисления, даже при замыкании пузырька с начальным радиусом R = 0,1 см при P 0 = 10³<< 1,3·10³ Па скорость замыкания от действия сил поверхностного натяжения увеличивается всего на 10 %. Поэтому наибольший практический интерес представляет учет влияниия сил вязкости и сил поверхностного натяжения для жидкостей со значительно большей вязкостью и поверхностным натяжением, чем у воды. При этом для вязких жидкостей уравнение приобретает вид

R = Re ( R + We ).                                                     (9)

Для жидкостей, близких по этим свойствам к воде, вязкость и поверхностное натяжение можно не учитывать.

Значительно большее влияние на скорость коллапса кавитационных пузырьков, особенно на последних стадиях, оказывает газосодержание, которое выражается удельным объемом растворенного газа, приведенным к атмосферному давлению

V ga

xA

Vm либо концентрацией – массой растворенного газа в единице объема жидкости m g

V , связными между собой (следуя закону Бойля - Мариотта Рд • Vg = Рй • Vga) соотношением

P

C = ^аР g • рт , ^g

Ощутимое количество газа δ > 0,5∙10-3, проникающее вследствие диффузии в кавитационные пузырьки, может содержаться лишь в очень маленьких пузырьках R < 1 мм, смы-– 373 – кающихся при малых значениях внешнего давления (P0 < 0,1 Pа). Поэтому растворенные в исследуемой сточной воде газы при нормальных условиях оказывают незначительное демпфирующее действие на скорость схлопывания пузырька. Наоборот, наличие в сточной воде твердой фазы, а именно взвешенных веществ, образующихся в результате окислительновосстановительных реакций частиц нерастворимых солей, увеличивает интенсивность кавитационно-кумулятивного воздействия, по-видимому, из-за увеличения степени турбулентных пульсаций в таких потоках.

Исследования воздействия гидротермодинамической кавитации позволяют получать наиболее адекватные результаты по воспроизводимости условий эксперимента, а также дают возможность проведения измерений физических параметров в кавитационной области. Заметим, что физико-химические эффекты идентичны независимо от способа возбуждения кавитации, что, безусловно, важно при решении вопроса о выборе СК-реакторов для определенных технологических решений.

Доказано [1 – 5], что в условиях гидротермодинамической кавитации протекают сложные физико-химические процессы, классифицируемые следующим образом:

• •    окислительно-восстановительные реакции с участием присутствующих в водной среде органических и неорганических веществ за счет образования в растворе Н₂О₂ и ОН;

• •    цепные реакции в растворе, инициируемые продуктами расщепления присутствующих в растворе примесей;

• •    деструкция макромолекул и инициирование деполимеризации полимерных соединений;

• •    реакции между растворенными газами внутри кавитационных пузырьков.

Для полученных математических моделей кавитации разработана математическая модель, связывающая параметры кавитационных эффектов с преобразованием примесей сточной воды и, как следствие, ее очистки. Для исследуемых режимов кавитации при газосодержаниях δ < 0,003 получена регрессионная модель, связывающая длину каверн L k , скорости вращения кавитационной крыльчатки W , давления P _∞, времени кавитационного воздействия t и снижение концентрации примесей С %. Чтобы увеличить при неизменной длине каверн все три параметра W , P _∞, С %, необходимо увеличить и загромождение потока – отношение площади сечения кавитатора к площади сечения потока – F k / F py . Анализ экспериментальных данных представлен в табл. 1, а регрессионная модель – на рис. 1.

Согласно литературным данным [1–7], в условиях гидродинамической кавитации можно условно выделить три зоны, где происходят химические реакции окисления:

• •    термодеструкция летучих соединений и образование ОН-радикалов на границе раздела жидкость – газ;

• •    термодеструкция летучих соединений и образование ОН-радикалов в газовой среде образовавшегося пузырька;

• •    зона в объеме жидкости, куда диффундирует небольшое количество ОН-радикалов, температура при этом на несколько порядков ниже температуры внутри пузырька.

Инициация радикально-цепных реакций окисления субстратов (химических загрязнителей органического происхождения) возможна при добавлении небольшого количества окислителя в зону кавитации, однако активация и кавитационное разложение молекул воды со- – 374 –

Таблица 1. Эффективность очистки сточной воды (модельный сток) при различных режимах кавитации

Показатель	Исходная концентрация, мг/дм3	Концентрация примесей после кавитационной обработки
		3000 об/мин			7000 об/мин			10000 об/мин
		30 с	60с	90с	30с	60с	90с	30с	60с	90с
pH	8.7	8,2	8,2	7,9	7,8	7,2	8,1	8,8	8,8	8,8
Cu	3,94	3,55	2,95	2,55	2,68	1,73	2,45	2,75	2,75	2,75
Zn	1,25	0,87	0,87	0,87	0,8	0,8	0,9	0,83	0,83	0,83
Pb	0,22	0,14	0,14	0,14	0,127	0,068	0,149	0,19	0,19	0,19
Fe	3,7	2,66	2,40	2,06	1,92	0,4	0, 6	2,66	2,66	2,66
Ni	2,52	1,58	1,58	1,58	1,53	0,63	1,43	1,86	1,86	1,86
Mn	0,03	0,02	0,02	0,02	0,015	0,003	0,005	0,02	0,02	0,02
Cr6+	0,012	0,01	0,01	0,01	0,004	0,004	0,004	0,01	0,01	0,01

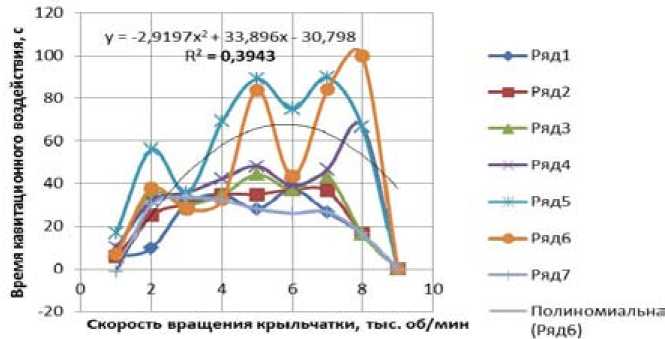
Рис. 1. Корреляционная зависимость эффектов очистки промышленного стока от режимов кавитации провождаются образованием сильных окислителей, таких как перекись водорода и озон, а следовательно, искусственное введение окислителей может быть целесообразным лишь с точки зрения сокращения времени кавитационной обработки стока.

Используя современные программные продукты для математического моделирования процессов в экспериментальном исследовании, получена модель оптимального подбора режима кавитационной обработки сточной воды с максимально возможным эффектом очистки по множеству нормируемых показателей, таких как рН, катионы тяжелых металлов, содержание микроорганизмов, общее солесодержание и ионы Fe. Математическая модель представлена на рис. 2.

В результате выполненных работ была построена комплексная математическая модель, связывающая процессы схлопывания кавитационных полостей, сопровождающиеся выбросом энергии, позволяющей преобразовать молекулы воды и модифицировать примеси стока.

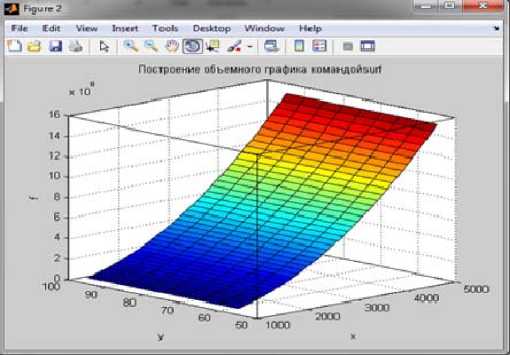
Рис. 2. Поле оптимальности ограничено числом вращения ротора кавитатора – минимально возможное 3000–5000 оборотов в минуту и временем кавитационного воздействия на сток – 60 секунд

Это позволит разработать комплекс рекомендаций по формированию технологического регламента применения кавитационных установок при кондиционировании промышленных сточных вод.

• [1]    Дубровская О.Г., Андруняк И.В., Приймак Л.В. Ресурсосберегающие технологии обезвреживания и утилизации отходов предприятий теплоэнергетического комплекса Красноярского края: монография. Красноярск: Сиб. федер. ун-т, 2014. 164 с.

• [2]    Дубровская О.Г., Евстигнеев В. В., Кулагин В.А. // Журнал СФУ. Техника и технологии. 2011 (4). № 6. 665–675.

• [3]    Евстигнеев В.В. Автореф. дис. … канд. техн. наук. Красноярск, 2012. 19 с.

• [4]    Дубровская О.Г., Евстигнеев В.В., Кулагин В.А. // Безопасность жизнедеятельности. 2012. № 3. С. 26–30.

• [5]    Kulagin V.A., Kulagina L.V., Kulagina Т.А. // Journal of Siberian Federal University. Engineering & Technologies. 2008. (1). Issue 1. 76–85.

• [6]    Дубровская О.Г., Кулагин В.А., Сапожникова Е.С. // Журнал СФУ. Техника и технологии. 2015 (8). № 2. 217223.

• [7]    Kulagin V.A., Sapoghnikova E.S., Feng-Chen Li et al // Journal of Siberian Federal University. Engineering & Technologies. 2014 (7). Issue 5. 605–614.