Математическое моделирование лазерно-локационного метода определения предельно малых концентраций углеводородов в приземном слое

На сегодняшний день зондирование земной поверхности посредством лазерных локаторов (лидаров) является перспективным и современным методом анализа и определения параметров компонентов окружающей среды, в том числе и при поиске углеводородного сырья [1]. Применение данного метода для геофизических исследований позволяет фиксировать локальные выходы природного газа, наблюдать пространственную динамику поверхностных утечек в реальном масштабе времени, осуществлять топологическую привязку предполагаемых месторождений к местности и др. Лазерно-локационные методы в сочетании с методами цифровой спутниковой съемки в течение последних лет активно применяются для решения подобных задач [2, 3].

Однако существующие методы и аппаратные средства позволяют определять только значительные утечки углеводородов (до 1 ppm), которые возникают, например, при прорыве нефте- и газопроводов. Данные решения не подходят для локализации вероятностных месторождений нефти и газа, поскольку для этих задач определяемая концентрация углеводородов в приземном слое является предельно малой (до 0.01 ppm). Проблемы повышения чувствительности метода определения концентрации углеводородов, позволяющего выявлять малые концентрации природного газа, возможно решить при адекватном математическом представления трассы распространения лазерного луча. Такая математическая модель позволит создавать высокоточные методы приема, оцифровки и компьютерной обработки принимаемых лидаром сигналов. Результаты разработки модели и метода обработки лидарных сигналов в свою очередь позволят создать интегрированный программноаппаратный комплекс, позволяющий осуществлять мониторинг предельных концентраций газа у земной поверхности с одновременной картографической привязкой. Установленный на базе летательного аппарата такой комплекс позволит с достаточно высокой точностью осуществлять разработку наиболее перспективных поисковых мероприятий за счет исключения "пустых" областей в исследуемых районах. Эта задача является особенно актуальной в условиях Сибири и арктических зон, где районы предполагаемых месторождений расположены в удаленных и труднодоступных местах.

АППАРАТУРА ДИСТАНЦИОННОГО ЗОНДИРОВАНИЯ

Авторами предложен программно-аппаратный комплекс для поиска предельных концентраций низших алканов в приземном слое [4–6]. Принцип функционирования разрабатываемого комплекса основан на методе дифференциального поглощения, подразумевающего сравнение обратно рассеянных лазерных сигналов: одного на частоте по- глощения, а другого — вне нее. Данный метод обладает высокой чувствительностью при определении молекулярных составляющих с больших расстояний.

Принцип работы лидара заключается в следующем. В качестве источника излучения в передающем блоке используются два лазерных генератора. Излучение поступает на формирующую оптическую систему передающего блока. Формирующая оптическая система осуществляет модуляцию излучения таким образом, что на выходе образуется последовательность чередующихся квазипрямоугольных импульсов по двум длинам волн, отличающихся по амплитуде. Промодулиро-ванное излучение направляется оптической системой на отражающий объект. Часть отраженного излучения улавливается приемным объективом и фокусируется на фотоприемном элементе (ИК-чувствительной матрице). При этом возникает переменный электрический сигнал, величина которого пропорциональна разности мощностей принятых импульсов излучения с длинами волн λ 1 и λ 2 .

Сигнал с приемной матрицы усиливается при помощи многокаскадного усилителя и поступает в микропроцессорный блок для обработки и синхронизации работы приемопередающего тракта.

Даже при сравнительно малом содержании исследуемого газа на пути лазерных лучей амплитуда сигнала с фотоприемника отразит степень содержания углеводородов в виде последовательности чередующихся импульсов. При этом излучение лазера с большой мощностью ослабляется на порядок сильнее исследуемым газом, и при значительной концентрации последнего на фотоприемнике будет также последовательность чередующихся импульсов разной амплитуды, но находящаяся в противофазе к последовательности посылаемых импульсов. Момент изменения фазы принимаемого сигнала на 180° характеризует определенное пороговое содержание природного газа, которое фиксируется микропроцессорной системой.

Из-за близости длин волн посылаемых импульсов, коэффициенты рассеивания на молекулах атмосферных газов и аэрозолях, а также коэффициенты отражения в данном спектре будут одинаковы. Таким образом, сравнение двух сигналов после регистрации собранного приемным объективом излучения дает меру интегрального содержания исследуемого газа вдоль оптического пути.

По результатам данных зондирования формируется перечень обнаруженных концентраций углеводородов в приземном слое с привязкой к местности, указывающий на наиболее вероятное расположение месторождения.

При этом основными проблемами регистрации малых концентраций углеводородов являются:

– во-первых, влияние ландшафта, т. к. в случае наличия густой растительности проведение замеров методом лазерного зондирования является неэффективным из-за того, что покров оказывает значительное влияние на отражение сигнала, в результате чего происходит большое количество ложных срабатываний;

– во-вторых, значительное рассеивание сигнала на молекулах атмосферных газов и аэрозолях при плохих погодных условиях.

Влияние ландшафта предполагается снизить за счет проведения исследований регионов крайнего севера, где отсутствует "тяжелый" растительный покров. Помехи, вызванные аэрозольным рассеиванием, предлагается снизить за счет динамической адаптации аппаратуры к изменяющимся в процессе зондирования условиям эксплуатации, высоте лета и пр. Для разработки технических и адаптационных требований к аппаратуре лидара, предложен математический аппарат, описывающий трассу прохождения лазерного луча.

МАТЕМАТИЧЕСКИЙ АППАРАТ

Лидарное уравнение для рассеяния, описывающее основные принципы лазерного зондирования приземного слоя имеет вид

P ( R ) = P • n • c • т • A ( R ) • MR • e "^{i : a} ‘ ⁽ ''d^- , (1)

где R — расстояние до рассеивающего объема (м); P λ ( R ) — мощность рассеянного излучения (Вт); β_λ ( R ) — объемный коэффициент обратного рассеяния атмосферы; α λ ( x ) — объемный коэффициент ослабления (экстинкции) атмосферы; c — скорость света (м/c); τ — длительность лазерного импульса (с); P 0 — мощность лазера (Вт); η — числовое значение КПД приемника; A ( R ) — эффективная площадь приемника (м²).

Объемный коэффициент обратного рассеяния атмосферы определяется суммой вкладов от газовой составляющей атмосферы и от содержащихся в ней частиц:

в , ( R ) = в а + в ь , (2)

где β _a — коэффициент рассеяния на газах; β _b — коэффициент рассеяния на частицах.

Коэффициенты обратного рассеяния атмосферы можно рассчитать с использованием конкретной модели атмосферы [7]. Для корректной оценки пропускания лазерного излучения атмосферой необходимо иметь информацию о физических и оптических моделях атмосферы.

По мнению авторов, одной из наиболее полных для решения задач дистанционного зондирования представляется физическая модель атмосферы, разработанная в Институте оптики атмосферы имени В.Е. Зуева СО РАН [4]. В ней, кроме профилей температуры, давления, концентрации H 2 O и O 3 для различных климатических зон, содержится информация о высотном распределении CO 2 , CO, CH 4, N 2 O, NO, NO 2 , а также сведения об их стандартных отклонениях для различных высот.

При значительной высоте лета и наличии препятствий на трассе лидара (трава, лесной покров и пр.), помимо коэффициентов обратного рассеивания и ослабления, важно учитывать длительность лазерного импульса и мощность лазера.

При выполнении замеров на объекте, скорость и высота лета которого являются динамическими параметрами, важно учитывать площадь телескопа (приемной антенны) и КПД приемника лазерного сигнала. Эффективная площадь приемника входит в лидарное уравнение для определения телесного угла, под которым приемник виден с расстояния R (при условии, что степень перехвата отраженного от приземного слоя лазерного пучка равна 1).

Ввиду того что разрабатываемый комплекс предполагается устанавливать на летательный пилотируемый или беспилотный аппарат, в целях экономии массы и электроэнергии в работе используются два гелий-неоновых лазера с низкими мощностями (до 1 Вт). Для компенсации низких мощностей в состав аппаратуры вводится многокаскадный усилитель для усиления принятого на приемный элемент сигнала. Но частотные характеристики усилителя вносят искажения в форму сигнала, и всякий раз, когда возникает собственный шум усилителя, он приводит к случайным возмущениям на выходе. Для определения максимально допустимой амплитуды и частоты шума, все шумовые помехи представлены в виде шум-фактора, характеризующего отношение номинальной мощности шума на выходе усилителя к шуму источника [8].

МОДЕЛИРОВАНИЕ ТРАССЫ ЛИДАРА

На основании предварительных исследований [4] можно сделать вывод о том, что описанная математическая модель позволяет обрабатывать отраженный от поверхности сигнал с учетом поглощения исследуемым в работе газом. Дальнейшее исследование модели позволяет определить максимальную высоту полета несущего летательного аппарата в режиме поиска при определенных метеорологических условиях, требования к минимальным метеорологическим условиям поиска, а также характеристики усиливающей аппаратуры, в частности предельной амплитуды шумовой составляющей сигнала.

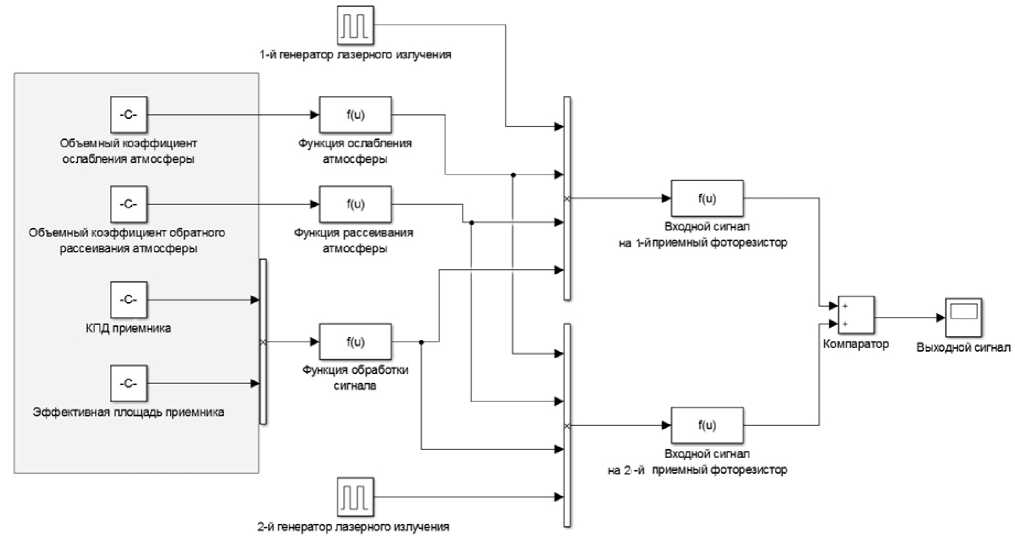
Рис. 1. Схема трассы лидара в среде Matlab

С целью определения вышеуказанных граничных условий в пакете прикладных программ Matlab было проведено моделирование трассы прохождения светового пучка. Модель включает 2 генератора лазерных импульсов. Генерируемые ими импульсы, отражаясь от зондируемой поверхности, попадают на приемные фотоэлементы (рис. 1). При этом мощность первого лазера на порядок выше, нежели мощность второго, и поглощается исследуемым газом.

Дальнейшая обработка и сравнение двух сигналов после регистрации собранного приемным объективом излучения дает меру интегрального содержания газа вдоль оптического пути.

Согласно [9], плотность взвешенных частиц воды в атмосфере для различных погодных условий составляет:

• -    чистый воздух — 0;

• -    совершенно ясно — 0.0005;

• -    очень ясно — 0.0011;

• -    ясно — 0.0024;

• -    легкая дымка — 0.0053;

• -    дымка — 0.0117;

• -    легкий туман — 0.0258;

• -    туман — 0.0567;

• -    плотный туман — 0.128 (сигнал не проходит назад).

Варьируя величиной R с шагом в 1 м и плотностью взвешенных частиц в соответствии с вышеуказанной информацией, были подобраны граничные условия для функционирования лидара (рис. 2). При этом необходимая величина принятого сигнала для возможности его обработки должна быть не менее 10 % от максимально возможного (высота лета 50 м, плотность взвешенных частиц 0) и составляет 0.4 В.

Анализ полученных результатов показал, что обработка сигнала с высотой лета аппарата от 150 до 200 м возможна только при ясной погоде (плотность взвешенных частиц должна составлять не более 0.005). При высоте лета не более 100 м, допускается применение лидара в дымке, при более высоких плотностях использование разрабатываемого комплекса является нецелесообразным ввиду невозможности обработки принятого сигнала.

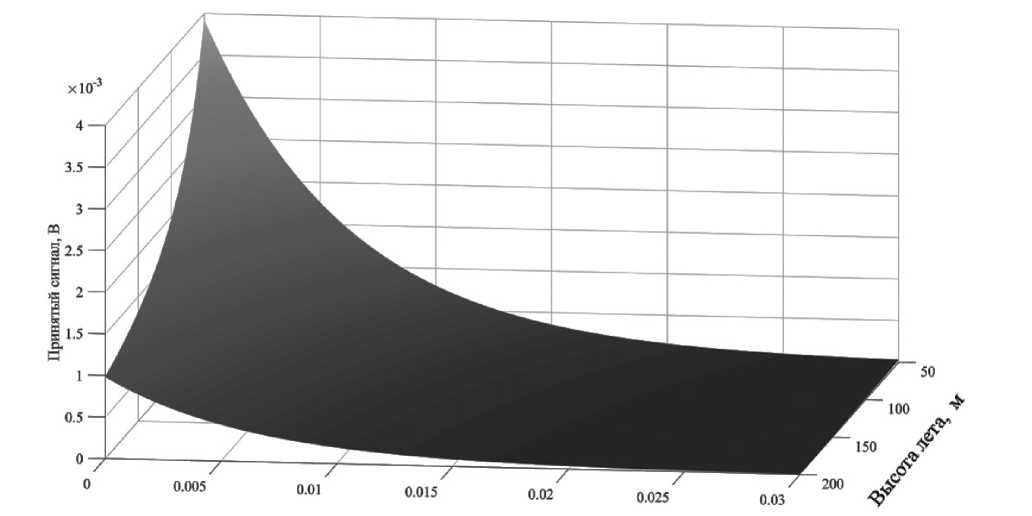
Плотность взвешенных частиц

Рис. 2. Результаты моделирования трассы лидара

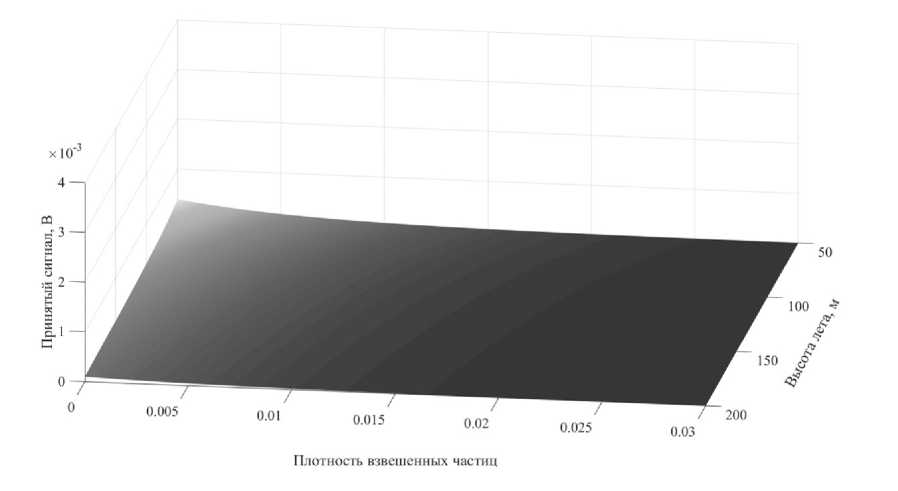
Рис. 3. Сгенерированный шум, наложенный на полезный сигнал

Поскольку при усилении сигнала происходит также и усиление шумов, создаваемых генератором напряжения (возникающих в свою очередь за счет нестабильного напряжения питания на летательном аппарате). Для определения максимально допустимого уровня шума в математической модели был промоделирован с помощью внутренних средств Matlab полностью зашумлен- ный сигнал путем добавления случайной помехи, равной по значению амплитуде выходного сигнала, т. е. усиление сигнала в данном случае полностью гасится паразитной помехой (рис. 3, 4). Для фильтрации сигнала в цепи используются фильтры подавления помех. Определено, что необходимая амплитуда принятого сигнала должна составлять не менее 0.4 В.

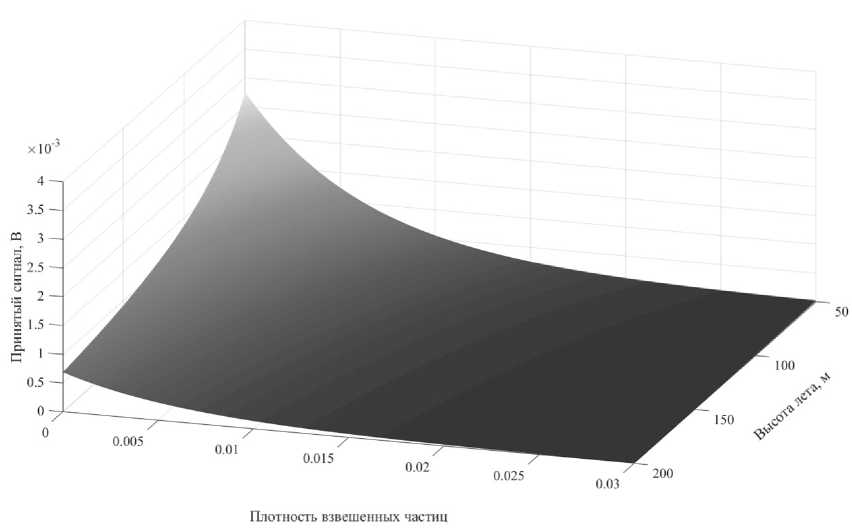
Рис. 4. Отфильтрованный сигнал

По результатам анализа выявлено, что для обеспечения читаемости принятого полезного сигнала на высоте от 150 до 200 м при ясной погоде необходимо обеспечить уровень шума относительно амплитуды не более 15 %. При этом допускается падение качества сигнала при выборе высоты лета до 100 м.

На основании проведенного моделирования трассы лидара сформулированы следующие ограничения:

• -    высота лета аппарата не более 200 м при ясной погоде и не более 100 м в дымке (плотность взвешенных частиц не более 0.005 и 0.0117 соответственно);

• -    зашумленность канала не более 15 % от амплитуды выходного сигнала.

ВЫВОДЫ

Изложенный в статье подход к определению предельно малых концентраций природного газа подразумевает создание методов лидарного авиационного зондирования, локализации и топологической привязки к местности предполагаемых месторождений с достаточно высокой точностью.

Предложенная математическая модель трассы лидара и применяемый метод дифференциального поглощения позволяют сформировать основные технические требования, определить условия эксплуатации и разработать аппаратуру для поиска предельных концентраций газа.

При проведении моделирования трассы лидара было выявлено, что:

• -    применение поискового комплекса в плохих погодных условиях (при коэффициентах видимости не менее 0.05) нецелесообразно, т. к. обработать полученный сигнал в этом случае не представляется возможным;

• -    высота лета, при которой остается возможность отследить изменение принятого сигнала в части его амплитуды, должна составлять не более 200 м при ясной погоде и не более 100 м в дымке;

• -    при разработке многокаскадного усилителя для усиления принятого на приемный элемент сигнала необходимым является система подавления помех, обеспечивающая зашумленность канала не более чем на 15 % от амплитуды входного сигнала.