Математическое моделирование многокомпонентных деформируемых сред

Первый постулат называется законом сохранения масс:

(I) V

Здесь /?(xi,x2,.V3,/) - плотность вещества.

Второй постулат - это закон изменения количества движения:

~ J р ^dV = J pFdV + J S^W ^dtv dt _y                  ■

Здесь v - вектор скорости, F - плотность массовых сил, У"* - поверхностная нагрузка, действующая на площадке с единичным вектором нормали п :

S'"’ - S.n,, 8,=а^                                        (3)

где а_у - компонента тензора напряжений. Мы будем рассматривать всюду малые деформации [2], гак что эйлеровы координаты совпадают с лагранжевыми. Все события происходят в пространстве Л'(0,?)х7?³(х₁,х₂,х₃) [3]. В пространстве R³ можно ввести радиус-вектор г [2]. Тогда постулат об изменении момента количества движения или кинетического момента можно записать в виде

—^rxp—dV^ jrxpFdV + ^r xS^'dL                   (4)

dt у dt у              £

Если рассматриваются неизотермические процессы, то следует привлечь законы термодинамики.

Первый закон термодинамики (закон сохранения энергии) может быть сформулирован в виде dE + dK = 5Q + 5A^,

где Е - внутренняя энергия среды, которая связана с плотностью внутренней энергии е соотношением

Е = ^pedE;

К - кинетическая энергия,

К = — J pv • v dE;

2 V

5Q - изменение внешнего притока тепла:

3Q = dt ^pqdE -J^"^ ,

где q- массовый источник тепла, q^- приток тепла через поверхность с единичным вектором нормали п =   :

q^ = q)nj;

(9.)

5А^- изменение работы внешних сил

(Ю)

Используя теорему живых сил

dK = 5AM + 5Av\ где 54(0- изменение работы внутренних сил

(И)

5Л⁽0 = dt jcr^dE,

a v - компоненты тензора скоростей деформации, равные

Vv=|(%+U-                      (13)

первый закон термодинамики (5) можно записать в виде dE = 5Q-5A^ .                             (14)

Внутренняя энергия Е и её плотность е являются функциями термодинамических параметров состояния, задание которых и определяет математическую модель среды.

Второй закон термодинамики

TdS = 5Q*W*dt

гарантирует существование ещё одной функции термодинамических параметров состояния - энтропии 5 или её плотности s :

S = ^pSdV.                                (16)

В формулировку второго закона термодинамики входит также функция рассеивания (диссипации) И-'* или её плотность и ’:

W* = J w'dV .                                     (17)

При этом для обратимых сред 1У * = 0 , а для необратимых И’ * > 0 При построении математической модели сплошной среды задают конкретное выражение функции рассеивания.

Первый закон термодинамики (5) или (14) может быть сформулирован в интегральном виде соответственно

di г

dt^.

		а--?	dV		, (18)
J V	/у+ ^F(G) ^“Чоыг		dV		(19)

Точно так же на основании (15) может быть дана интегральная формулировка второго закона термодинамики

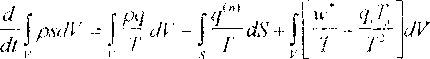
Можно дать дифференциальные следствия из интегральных формулировок основных постулатов МСС. Так из закона сохранения масс (1) следует уравнение неразрывности

—+ div(/?v)=o(21)

Из закона об изменении количества движения (2) следуют уравнения движения сплошной среды в векторной форме dv , о

,>     ■ /V ■(22)

dt или в компонентах p-^ = pF„^o(23)

dt

Из закона об изменении кинетического момента (4) следует симметричность тензора напряжений а :

Дифференциальным следствием первого закона термодинамики является уравнение

=          -v + pq-Чи            (25)

ИГ        иг из интегральной формы (18) и de

Р-р^^РЧ-Ч.,                      (26)

из интегральной формы (19).

Дифференциальным следствием второго закона термодинамики (20) является уравнение ds pT-— pq-q,^ ■( dt

Уравнение (27) называется уравнением притока тепла. Обычно полагают справедливым классический закон теплопроводности Фурье

Ч> = -МГр(28)

где А- тензор теплопроводности. Для изотропной среды

^=^5ii.(29)

Таким образом, для однородной изотропной среды уравнение притока тепла (27) имеет вид рТ~ - КМ + pq + w’.

• §2 . Основные уравнения для многокомпонентной среды

Для многокомпонентной среды некоторые постулаты приходится изменить. В связи с этим изменяются и основные уравнения.

Пусть каждая частица сплошной среды содержит m подчастиц (компонентов). Каждый компонент имеет плотность р^Р, а-Л,...,т Суммарная плотность частицы вещества равна р:

Р =                                                  (1)

Скорость каждого компонента обозначим через г(я\ Тогда скорость каждой частицы сплошной среды v можно представить как центр масс подчастиц.

Определим диффузионный поток 3^ формулой [4]

Из (1)-(3) следует, что

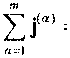
Введём величину массовой концентрации компонента а :

Из (1) и (5) следуег, что

В литературе встречаются и другие характеристики, описывающие концентрацию вещества [5]. Например, объёмная концентрация

V“> -yWjy                                    (7)

т. е. отношение объёма, занимаемого компонентом а, ко всему объёму И ; молярный объём компонента где N'"1 - число частиц компонента а . Количество частиц, приходящееся на единицу объёма,

п(п)

и т.п.

Иначе вводятся и диффузионные потоки. Например, i(a) = „(ЮуСЮ .                                             (Ю)

В отличие от (4) сумма этих потоков не равна нулю, но

.                                                     (11)

rrl

В многокомпонентной среде могут происходить химические реакции со скоростями J,, I = V2,...,N. Пусть г'^-коэффициенты, пропорциональные стехиометрическим коэффициентам а = 1,2,..., т . Тогда для каждого компонента будет изменяться и постулат (1.1), который для каждого компонента может быть записан в виде

^p^W^Rady.(12)

dl I

Соответствующее уравнение неразрывности для компонента а имеет вид

,(13)

где

+div^V^(14)

Просуммировав уравнения (13) по всем компонентам, получим на основании (1) и (2) уравнение неразрывности (1.21) для всей частицы. При этом очевидно

Уравнения (13) запишем несколько в другом виде. Для этого добавим в левую часть

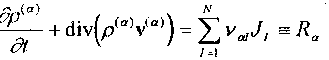
а также добавим

(13) и вычтем из неё выражение нулевое слагаемое

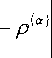
1 dp „ --— + div v р di

тогда имеем

= —— + йд(/Г“'Г“!                — ™divv =

St                            VP ^

®P. — + divL⁽X^<“⁾-‘')]⁺Xr T/Z^v -p^v_H ~~—— -p^v_H =

St                                              p dt dt             p dt dpw d / H\ dt dr '

Поэтому вместо уравнения (13) получим эквивалентное ему p—- + dwiw =Ra .

at

Заметим, что уравнения, аналогичные (13), (18), для других концентраций имеют вид:

+ div^v^) -( dt      v’ м

-- + div(®(a)i(a)) = ^ ,(20)

St      х      ’   Мо где Ео - молярный объём, Мо - средняя масса грамм-молекулы вещества.

Определяющие соотношения процесса диффузии задаются первым законом Фика [6], как связи между диффузионными потоками (* -y 1 > 1 ) и градиентами соответствующих концентрации вещества данного типа \п »1 ,с ) Эти определяющие соотношения связывают (/и-1) независимых векторов диффузионных потоков с (т -1) градиентами независимых концентраций.

Если обозначить через 7*'^-массовые силы, действующие на каждый компонент композита, то суммарные массовые силы F естественно представить в виде pI^^p^F^V                           (21)

Мощность этих сил может быть в соответствии с (3) представлена следующим образом

£ д“>F^,“^, ■ v^(ui = 2 F^(a) ■ Г* + pF- v

Выражение мощности фигурирует только в постулате, представляющем собой закон сохранения энергии (первый закон термодинамики). Поэтому из пяти рассмотренных в предыдущем параграфе постулатов (1.1), (1.2), (1.4), (1.18) или (1.19) и (1.20), изменениям для многокомпонентной среды кроме постулата (1.1) может подвергнуться только постулат (1.18) или (1.19).

Запишем вместо (1.18) для многокомпонентной среды

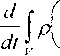
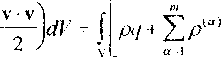
dv +J[s(n,-v-^"'И

а вместо (1.19) согласно (1.11) и (22) •

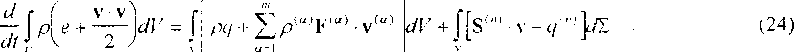
Тогда дифференциальным следствием (23) будет уравнение

V . S Х ,/К/                     (25)

а дифференциальным следствием (24) - уравнение р + Е F ■ j(a) + рч ~ ^‘               а-Л

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (96-01-0084), а также Федеральной целевой программой "Интеграция" (проект №426).