Математическое моделирование многокомпонентных перемещений и оптический метод их измерения

перемещений контролируемых объектов и разработки их метода измерения.

Вопросы моделирования сложных многокомпонентных перемещений простых и достаточно простых объектов решались в ряде работ еще в девяностых и нулевых годах [3-7]. Вопросы моделирования многокомпонентных перемещений сложных объектов выходят за рамки настоящей работы, однако одним из приложений развиваемого подхода является задача калибровки манипуляторов универсальных промышленных роботов, которые, несомненно, могут быть отнесены к классу сложных механических систем [8]. Модели сложных перемещений шестизвенных манипуляторов еще более усложняются, однако моделирование многокомпонентных перемещений составляющих цепочку манипулятора звеньев может рассматриваться как моделирование многокомпонентных перемещений простых объектов далее встраиваемых в более сложные модели всего манипулятора [9]. Поэтому принципиальное значение имеет вопрос обоснования и разработки общей идеологии моделирования сложных многокомпонентных перемещений простых или достаточно простых, но деформируемых объектов, с целью выявления компонентов перемещений и деформаций, источниками которых могут служить совершенно различные факторы. Соответственно, отдельные компоненты таких многокомпонентных перемещений и деформаций носят информативный характер и могут являться измеряемыми величинами. Осознание этой проблемы привело к созданию концепции векторных многокомпонентных физических величин, базирующейся на следующих трех положениях [4-7]:

. векторные многокомпонентные физические величины рассматриваются как вектор-функции множества составляющих их информативных компонентов;

. функции связи названных информативных компонентов в моделях многокомпонентных физических величин определяются законами векторной алгебры;

. информационные модели векторных многокомпонентных физических величин допускают многовариантность представления указанных информативных составляющих в зависимости от объекта исследования и поставленной задачи.

Перечисленные положения являются основой для построения моделей многокомпонентных перемещений и деформаций подвижных объектов, отражающих сложные процессы, происходящие с движущимися объектами.

ОБОБЩЕННЫЕ МАТЕМАТИЧЕСКИЕ МОДЕЛИ СЛОЖНЫХ МНОГОКОМПОНЕНТНЫХ ПЕРЕМЕЩЕНИЙ ПОДВИЖНЫХ ОБЪЕКТОВ

В общем виде математическая модель векторной многокомпонентной физической величины, включающая в себя информативные компоненты и отражающая сложные процессы, происходящие с движущимся объектом, в декартовой системе координат представляется следующим образом:

X x (r,T )   F(x1 x (r,T ) ’•••’ xpx (r,T ));

X y ^{( r , T} ) = F ( x i y ^{( r , T} ) ,..., x py ( r , ^ ) ) ; - X z ⁽ r , T ) = f ( x i z ⁽ r , t ) ,,„, x pz ⁽ r , T ) ) ,

где X _x ( r , T ) , X y ( r , T ) , X _z ( r , T ) - проекции многокомпонентных перемещений на координатные оси декартовой системы координат; x i k ( r , T ) ,•••, x pk ( r , T ) - информативные компоненты k -й координатной составляющей ( k e { x , y , z } ) многокомпонентного перемещения X ; r , T - пространственные и временные координаты; F – функция связи, определяемая физикой исследуемого объекта или процесса.

В случае линейности модели (1) в соответ- ствии с перечисленными положениями векторной многокомпонентной физической величины она представляется в виде векторной суммы соответствующих информативных составляющих (компонентов):

ppp

где 2 xjx(r,T), 2 xjy(r,T), 2 xjz(r,T)- j=1

j• = 1

j = 1

векторные суммы p информативных компонентов координатных составляющих величины X .

Модели (1) и (2) отражают системный взгляд на проблему представления сложных перемещений подвижных объектов, направленный на сведение многообразия имеющих место информативных компонентов названных величин в единую теоретическую картину.

Поскольку информативные компоненты x jx ( r , T ) , x jy ( r , T ) , x j _z ( r , T ) , зашитые в модели (2) представляют интерес, они должны быть измерены. Проблема кроется в самой природе этих величин. Они имеют одинаковую физическую размерность, перекрывающийся в значительной степени или совпадающий спектральный диапазон, и поступают на входы измерительных устройств в виде векторных сумм X _x ( r , T ) , X y ( r , T ) , X _z ( r , T ) . Поэтому известные методы и средства измерения не селективны по отношению к составляющим их компонентам x jx ( r , T ) , x jx ( r , T ) , x j _z ( r , T ) . Решение обозначенной проблемы предложено на основе организации информационной избыточности на входе измерительных устройств [10].

МЕТОД МНОГОМЕРНЫХ ТЕСТОВЫХ ОБЪЕКТОВ

Сущность метода многомерных тестовых объектов сводится к тому, что для обеспечения процесса измерения информативных составляющих перемещений контролируемого объекта оптическим методом с объектом связывается распределенный в пространстве контрольный объект, обладающий известными с высокой точ- ностью геометрическими параметрами, которые используются в процессе реализации метода в качестве мер [11]. Особенностью метода является то, что параметры многомерного тестового объ- екта отражают многомерность контролируемых перемещений и функционально связываются с ними в процессе формирования моделей для дальнейшей реализации метода. Соответственно в модель (1) вводятся математические объекты L1 k,..., Lqk, отражающие использование нового физического объекта, получившего название

^X x ^{( r , T} ) = 2 ^x jx ^{( r , T} ) ;

j = 1

Z X P Z X

^X y ^{( r , T} ) = 2 ^x jy ^{( r , T} ) ; ^ j = 1

p

^X z ^{( r , T} ) = 2 ^x jz ^{( r , T} ) , j = 1

тестового:

X x ^{( r} ,^{T ) = F ( x} 1 x ^{( r ,T} ) , X y ( r ,T ) = F ( x 1 y ( r ,T ) ,.

X z ^{( r ,T ) = f ( x} 1 z ^{( r ,T} ) ,

•, ^x px ⁽ r ,^T ) , ^L 1 x ,, ^x py ⁽ r ,^T ) , ^L 1 y ,-

^-, ^x pz ⁽ r ,^T ) , ^L 1 z ,^-

^-, ^L qx ) ^;

^-, ^L qy ^{) ;} ' ⁽³⁾

L )

^-, ^qz /, J

где L 1 k ,..., L qk — компоненты k -й координатной составляющей L _k многомерного теста L ; q - количество компонентов k -й коор-

динатной составляющей L _k многомерного теста L ; F – функция связи компонентов ^x 1 k ^{( r} ,^T ) ..... x pk ^{( r ,T} ) и L 1 k ,-, L qk кооРДи-натной составляющей L k ( k e { x , y , z } ) многомерного теста L .

Таким образом, модель (3) по сравнению с моделью (1) является информационно избыточной за счет ввода в нее компонентов L i k ,..., L qk , связанных с параметрами многомерного тестового объекта.

Проводя аналогию между параметрами (составляющими) многомерного тестового объекта и составляющими сложных перемещений, компоненты многомерных тестов или их проекции на координатные оси будем рассматривать как многокомпонентные величины - многокомпонентные тесты, составляющие которых также являются векторными величинами. Соответственно, общая методика формирования многомерных тестов и функции связи их компонентов с моделируемыми величинами подпадают под основные положения концепции векторных многокомпонентных физических величин и формулируются следующим образом:

. многомерные многокомпонентные тесты – векторные величины и рассматриваются как функции множества составляющих их компонентов;

. функции связи названных компонентов в моделях многокомпонентных тестов определяются законами векторной алгебры;

. модели векторных многомерных многокомпонентных тестов допускают многовариантность представления указанных составляющих в зависимости от решаемой задачи.

Опираясь на приведенные положения о многомерном тесте, формируемом на базе многомерного тестового объекта, можно определить вид функции связи информативных компонентов x i k ( r ,т ) ..... x pk ( r .т ) и компонентов L i k ,..., L qk k -й координатной составляющей L _k многомерного теста L в модели (3):

{ x.y.z q { x,y,z } p

= Z Z viuk L iuk + Z Z nyk x ijk ( r ,T ) , (4) ku = 1 k j = 1

где i – порядковый номер функции связи; k e { x , y , z } - множество координатных составляющих; u – порядковый номер компонентов многокомпонентного теста L _iuk ; j – порядковый номер информативных компонентов к -й координатной составляющей многокомпонентного перемещения X k ( r , т ); V iuk e [ 0,1 ] - весовые коэффициенты, отражающие отсутствие – 0 – или наличие - ( 0,1 ] - соответствующей компоненты многокомпонентного теста L _iuk в модели (4);

nyk e [ 0,1 ] - весовые коэффициенты, отражающие отсутствие - 0 - или наличие - ( 0,1 ] - соответствующей информативной компоненты x ijk ( r ,т ) в модели (4).

Используя (4), можно представить модель (3) следующим образом:

Xix q                        1 (r ,Т )   Z viuxL iux + Z 4ijx x ijx (r,T ); u=1            j =1 Xiy qp (r,T )= Z viuy L iuy + Z nijy x ijy (r,T ); u =1             j=1 I(5) Xiz qp (r ,T )= Z viuz L iuz + Z 4ijz x ijz (r ,T ), u =1            j=1 где векторы Liux , Liuy , Liuz , xijx , xijy , xijz определены в одномерных пространствах, совпадающих с соответствующими осями декартовой системы координат.

Такое представление модели (3) дает меха- низм адаптации к конкретным задачам за счет комбинирования коэффициентов vi-ux e[0,1], viuy e [0,1], Viuz e [0,1], nijx e [0,1], nijy e [0,1], nijz e [0,1]. Комбинирование значений весовых коэффициентов, принимающих значения из области их определения, позволяет формализовать и в перспективе автоматизировать процесс построения моделей для различных практических приложений [12].

С целью формализации процедуры генерирования моделей введены специальные комбинационные коэффициенты, принимающие значения в соответствии со следующим соглашением [11,13]:

+1, если проекции векторов L i-uk , Xjk совпадают с направлени ем соответ - ствующей оси координат ;

^ iuk , ^ ijk

-1, если проекции векторов L iuk , не совпадают с направлени ем x ijk (6)

соответствующей оси координат , 0, если соответствующая компонента отсутствует

С учетом соглашения (6) модель (5) приобретает вид:

qp

Xix (r ,т )= Z 5 iuxviuxLiux + Z S ijx njjxxijx (r ,т ); u=1

qp

X iy (r,T)= Z 5iuyviuyLiuy + Z Sijy nijyxijy (r,T) ; ” u=1

qp

Xiz (r,T)= Z 5iuzviuz Liuz + Z Sijznijzxijz (r,T) • I u=1

Каждое из уравнений модели (7), являющихся проекциями моделируемой величины на соответствующую координатную ось декартовой систе- мы координат, является моделью перемещения точек объекта в одномерном пространстве.

Полученные модели использованы в процессе оптических измерений информативных составляющих многокомпонентных перемещений на основе метода многомерных тестовых объектов [2,6,11]. Методообразующие признаки метода измерения следующие:

Наличие (возможность сформировать) системы из n уравнений, асимметричных относительно информативных компонентов х 1 _k ( r , г ) ,..., х _pk ( г , г ) ( k е { x , y , z } - множество координатных составляющих) перемещений соответствующих точек изображения тестового объекта:

Y 1 ^{( г , г} ) = ¥ 1^1 ^{{ х} 1 k ^{( г , г} ) , ..., ^х pk ^{( г , г} ) , L 1 k ,..., L qk ^}} ; '

Y n ^{( г} , ^г ) = Y n ^{ F p ^{{ x} 1 k ^{( г , г} ) , ..., ^х pk ^{( г , г} ) , L 1 k , ..., L qk ^{}} ,} _

^{( n} >  P >  ^{2 )} ,                       (8)

F 1 ^{{ x} 1 k ^{( г , г} ) , -, ^х pk ^{( г , г} ) , L 1 k , ...^{, L} qk ^} * ...^:

... ^ F p ^{{ x} 1 k ^{( г} , ^г ) ,..., ^х pk ^{( г} , ^г ) , ^L 1 k , ..., ^L qk ^} , ⁽⁹⁾ где Y 1 ( г , г ) ,..., Y _n ( г , г ) - функции пере -мещений соответствующих точек изображения контролируемого объекта относительно выбранных(ой) на изображении точек(чки) отсчета; F 1 ^{{ х} 1 k ^{( г} , ^г ) ,-, ^х pk ^{( г} , ^г ) , ^L 1 k ,-, ^L qk ^} ,..., F p ^{{ х} 1 k ( г г ) ,..., x pk ( г г ) , L k , — , L qk ^{} - многоком-}понентные векторные функции множества составляющих их информативных компонентов ^х 1 k ^{( г} , ^г ) ,..., ^х pk ^{( г} , ^г ) и компонентов L 1 k ,..., L qk k -й координатной составляющей L _k многомерного тестового объекта (многомерного теста) L .

Реализуемость специальных измерительновычислительных алгоритмов:

^х 1 k ^{( г , г} ) = f l ^{{ y} 1 ^{( г} , ^г X..., ^Y n ^{( г} , ^{г )}} ; '

Очевидно, что при использовании одноканальной оптической системы ее коэффициенты передачи Vi,..., V n одинаковы. Введем коэффициент передачи оптического преобразователя ст. Тогда система уравнений (8) может быть записана в следующем виде:

Y 1 ( ^{г , г} ) = r r i F , ^{{ х} , k ^{( г , г} ) , ..., ^х pk ^{( г , г} ) , L 1 k , ..., ^L qk ^}} ;

Y n ^{( г} , ^г ) = ^{ct {} F p ^{{ х} 1 k ^{( г , г} ) , ..., ^х pk ^{( г , г} ) , L 1 k , ..., ^L qk ^}} ,

( n >  p >  2 ) .                     (12)

Вид функций связи информативных компонентов х 1 k ( г ,т ) ,..., х pk ( г ,т ) и компонентов L 1 k ,..., L qk k -й координатной составляющей L _k многомерного теста L в модели (12) определяется выражением (4).

Используя механизм комбинирования коэффициентов v iux е [ 0,1 ] , ^v i _U y е [ 0,1 ] , ^vi _UZ е [ 0 ^{,1 ]} , ⁿ ijx ^{е [ 0},^{1 ]} , ⁿ ijy ^{е [ 0},^{1 ]} , ⁿ ijz ^{е [ 0,1 ]} , соглашение (6), введенное для формирования модели (7), а также соглашение для J i :

+ 1, если проекции векторов Y^ ( г , г )

совпадают с направлени ем соответ - ствующей оси координат ;

- 1, если проекции векторов Y^ ( г , г )

противопол ожны направлени ю соответств ующей оси координат систему уравнений (12) представим в следующей скалярной форме:

f { x , y . z } q                        { x , y . z } p

Y 1 ^{( г} ) = - Г 1 ^ст ] S Z ^ 1 uk v 1 uk L uk ⁺ X I ? 1 jk n 1 jk x jk ^{( г} )

I ku = 1               k j = 1

f { x , У . z } q                         { x , y . z } p

Y n ^{( г} ) = ^-7 n ° ] ^{S S} ^ nuk v nuk L uk ^{+ S S} ^ njk ^ njk x jk ^{( г} )

I ku = 1                k j = 1

( n >  p >  2 ) .                   (14)

^ (10)

^х pk ^{( г , г}) = f p ^{{ Y} 1 ^{( г} , ^г X ..., ^Y n ^{( г} , ^{г )}} ,

условием существования которых, при непрерывности и дифференцируемости

Y 1 ( г , г ) ,..., Y _n ( г , г ) во всем диапазоне измерения, является неравенство нулю Якобиана:

det

^{d Y} i ^{( г} , ^г ) а ^х k ^{( г} , ^г )

* о

г = 1, n , j = 1, p . (11)

Условие (11) обеспечивается реализацией «асимметрии» величин Y ^ ( г , г ) ,..., Y _n ( г , г ) относительно составляющих их компонентов х 1 k ( г , г ) ,..., х pk ( г , г ) и L 1 k ,..., L qk , которая выражена неравенством (9).

где Y 1 ( г ) , ..., Y_n ( г ) - расстояния от выбранных на чувствительной плоскости приемника изображения точек начала отсчета (меток) до i -х точек изображения контролируемого объекта [2].

Условие (11) существования соответствующих измерительно-вычислительных алгоритмов, получаемых из (14), будет выглядеть следующим образом:

det

d Y(г)

8 ^xk ^(г )

^ 0 i = 1, n , j = 1, p .

Решая систему уравнений (14) относительно x 1 k ( г ) ,..., x pk ( г ) , в аналитическом виде получаем соответствующие измерительно-вычислительные алгоритмы:

x к ^(т ) = f 1 ^{ Y 1 ^{( т)} ..., Y n ^{( т )}} ; '

x pk ^(т ) = fp ^{{ Y} 1 ^{( т} ) , ..., Y n ^{( т )}} .

Данные алгоритмы, представленные в виде аналитических выражений, могут содержать знак «-», наличие которого несет информационное содержание, обусловленное принятыми ранее соглашениями (6) и (13). А именно, знак «-» перед значением соответствующей информативной компоненты x jk ( т ) говорит о направлении вектора перемещения, противоположном направлению соответствующей координатной оси.

ТЕСТОВЫЕ ОБЪЕКТЫ И ФОРМИРОВАНИЕ МНОГОКОМПОНЕНТНЫХ ТЕСТОВ

В МОДЕЛЯХ МНОГОКОМПОНЕНТНЫХ ПЕРЕМЕЩЕНИЙ

Вопросы формирования тестовых объектов, их классификация, оптимизация их количества и качества в моделях должны составлять предмет отдельных исследований, поскольку от них зависят и теоретические возможности, и практические применения [14]. Тем не менее, для полноты представления теоретического материала приведем примеры формирования тестовых объектов и использования их параметров при формировании тестов в моделях (5).

Учитывая, что рассматриваемые перемещения являются многомерными, то и тестовые объекты должны являться многомерными. Частным случаем многомерного тестового объекта является одномерный тестовый объект, который показан на рис. 1 в виде отрезка прямой AB .

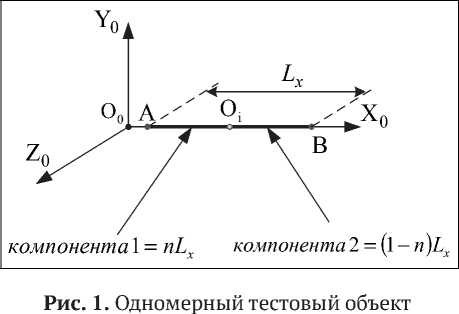
Тестовый объект в виде отрезка AB , показанный на рис. 1, можно рассматривать как одномерный однокомпонентный или как одномерный многокомпонентный.

В первом случае учитывается то, что отрезок AB размещен вдоль оси О ₀X₀ , проецируется на плоскость О 0 Y 0 Z 0 в точку и имеет один геометрический параметр – длину L_x . Во втором случае во внимание принимаются компоненты АО i = n L_x и O i B = ( 1 - n ) L_x , n e ( 0, 1 ) .

Один из таких объектов, показанный на рис. 1, был использован в процессе решения конкретной задачи определения составляющих многокомпонентных перемещений подвижного объекта [15]. В частности, там параметрами тестового

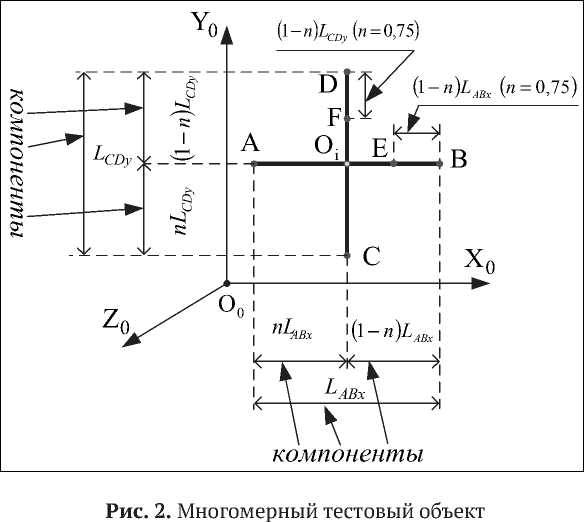
Поскольку общая методика формирования многомерных тестов и функции связи их компонентов с моделируемыми величинами подпадают под основные положения концепции векторных многокомпонентных физических величин, то в общем случае тестовый объект является многомерным, а одномерный и двухмерный (плоский) объекты являются частными случаями. При этом просматривается огромное количество распределенных в пространстве объектов, которые могут рассматриваться в качестве тестовых. Более того, об этом также уместно сказать заранее, что и сам контролируемый объект может рассматриваться при выполнении определенных условий в качестве тестового. Однако формальное конструирование тестового объекта вне связи с вопросами физической реализуемости метода измерения бессмысленно. Поэтому представленные на рис. 1 и рис. 2 объекты являются примерами, несомненно, не исчерпывающими полноту пространства существования тестовых объектов в области существования решаемых данным методом задач.

РЕАЛИЗАЦИЯ МЕТОДА

Как отмечалось в работе [14], представленные основы метода многомерных тестовых объектов являются базой для построения оптических информационно-измерительных систем определения составляющих сложных многокомпонентных перемещений подвижных объектов, позволяя в рамках метода решать некорректную задачу восстановления реальных координат движущегося объекта по его плоскому изображению. Громоздкость рассмотренных моделей и кажущаяся трудоемкость метода обусловлены сложностью и информационной насыщенностью измеряемых перемещений и желанием полностью формализовать процесс поиска соответствующих измерительно-вычислительных алгоритмов.

Для иллюстрации работы метода синтезируем измерительно-вычислительные алгоритмы для оптической измерительной системы определения информативных составляющих перемещений подвижного объекта.

С этой целью рассмотрим графическую модель сложных перемещений подвижного объекта, представленную на рис. 3.

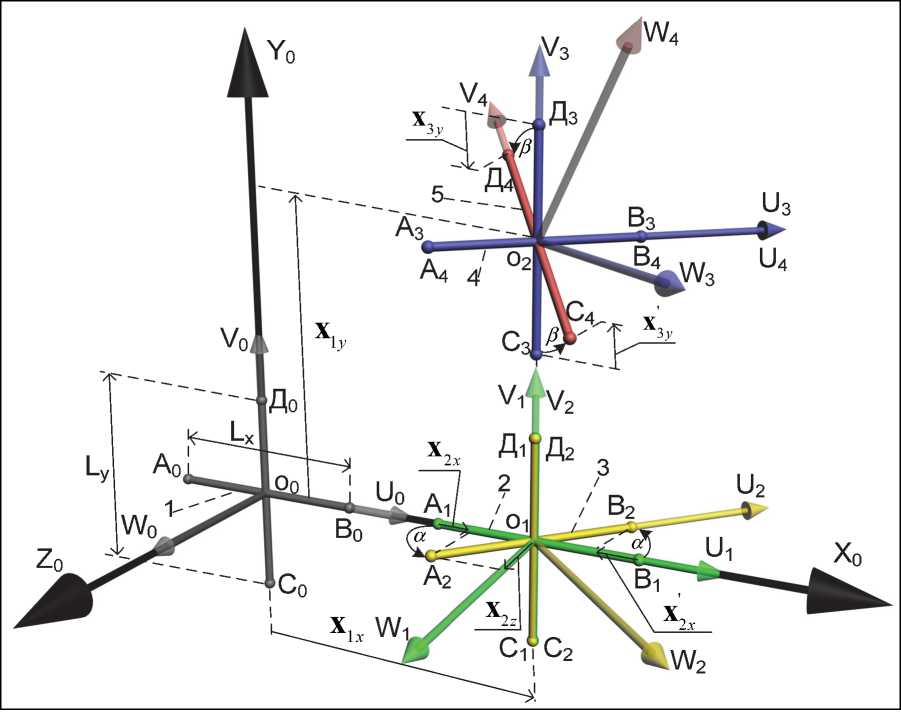
Рис. 3. Графическая модель перемещения тестового объекта ABCД: L_x , L_y – известные параметры тестового объекта; 1, 2, 3, 4, 5 – положения тестового объекта, полученные путем декомпозиции результирующего перемещения; x 1 x , x ₂ x , x' ₂ x , x 1 _y , x _{3 y} , x' _{3 y} - информативные компоненты результирующего перемещения тестового объекта

В соответствии с требованиями метода с перемещающимся объектом совмещен многомерный тестовый объект АВСД с известными геометрическими параметрами L x и L y . Осуществляя декомпозицию сложного перемещения объекта ABCД на информативные составляющие, примем следующие обозначения. В начальный момент времени тестовый объект ABCД обозначен А₀В₀С₀Д₀ , его центр О о совпадает с началом системы координат { O o ,X q ,Y q ,Z o } , а его стороны А о В о и С о Д о совпадают с координатными осями О 0 X 0 и О ₀ Y₀ , соответственно. Начальное положение объекта обозначено цифрой 1. В конечном положении, обозначенном цифрой 5, тестовый объект обозначен А₄В₄С₄Д₄ . Произведя декомпозицию результирующего перемещения тестового объекта из положения 1 в положение 5 на информативные составляющие, можем перейти к следующему этапу.

Для удобства описания используем присоединенную к тестовому объекту систему координат { О i ,U i,Ni ,W i } . Информативные компоненты результирующего перемещения удобно представить в виде матриц перехода от присоединенной к тестовому объекту системы координат в каждом из положений объекта:

{ О o ,U o ,V o ,W o 1 > - >Ю i ,U i ,V i ,W i } > -- ^ { О 4 ,U 4 ,V 4 ,W 4 } .

Тогда переход тестового объекта ABCД из положения 1 в положение 5 можем представить преобразованием системы координат { О o ,U o ,V o ,W o } в систему координат { О 4 ,U 4 ,V 4 , W 4 } путем:

. перехода из системы координат { О o ,U o ,V o ,W o } в систему координат { О^^, V i , W i } смещением первой в направлении оси О₀X₀ на величину x _{1 x} ;

. перехода из системы к о орди -нат { О^^, V i , W i } в систему координат { О 2 ,U 2 ,V 2 ,W 2 } поворотом вокруг оси О^ на угол а ;

. перехода из системы координат { О 2 ,U 2 ,V 2 ,W 2 } в систему координат { О 3 ,U 3 , V 3 W 3 } смещением ее в направлении оси О₁V₂ на величину x _{1 y} ;

. перехода из системы координат { G 3 ,U 3 ,V 3 ,W 3 } в систему координат { О 4 ,U 4 ,V 4 ,W 4 } поворотом первой вокруг оси О 2 U 3 на угол р .

Однородные матрицы перехода, описывающие названные перемещения, имеют следующий вид:

	г 1	0	0	x i x
	0	1	0	0
Т У 0 , x i x =	0	0	1	0
	. 0	0	0	i _

	cos а	0	sin а	0 "
	0	1	0	0
T V i , а =	- sin а	0	cos а	0
	. 0	0	0	i _

100 0

Ty = T V 2, x i у	0 0	1 0	0 1	x i у 0
	0	0	0	i

	г ,	0	0	0 "
T y 3 , в =	0	cos в	sin в	0
	0	- sin в	cos в	0
	. 0	0	0	i _

Матрица (17) описывает компоненту, характеризующую поступательное перемещение объекта в направлении оси О 0 X 0 (вектор перемещения x _{1 x} ). Матрица (18) описывает компоненту, характеризующую поворот объекта вокруг оси

О^ (угол поворота а ).Матрица(19) описывает компоненту, характеризующую поступательное перемещение объекта в направлении оси О 0 X 0 (вектор перемещения х , у ). Матрица (20) описывает компоненту, характеризующую поворот объекта вокруг оси О 2 U 3 (угол поворота в ).

Соответственно, однородная матрица композиции преобразований, описывающая результирующее перемещение объекта АВСД из положения 1 в положение 5, имеет вид:

T 5

= ^Т У о , x x 1 T V,а ^T V 2 , x i у ^Т У 3 , в ,

где каждая из матриц перехода несет информацию о соответствующих информативных составляющих сложного перемещения объекта АВСД.

В общем случае перемещающийся объект имеет шесть степеней свободы. Следовательно, в однородной матрице композиции преоб-разований будет представлено шесть матриц перехода в каждом такте измерения. Например:

ⁱ T 7 = Т у 0 , x , x T V^ T V,. . . у Т у 3 , e T W 4 , -x iz T W^

Переходя от реального объекта АВСД к его изображению в системе машинного зрения, мы переходим от пространственных координат точек ( X, Y, Z ) контролируемого объекта к их двухмерным изображениям, где для обозначения координат пикселя используется сокращенная запись ( x , у ) .

Рассмотрим задачу определения информативных компонентов, описанных однородной матрицей композиции преобразований (21) для перемещения объекта АВСД из положения 1 в положение 5, как показано на рис. 3. В соответствии с принятыми обозначениями векторы x _{1 x} и x _{1 y} , характеризующие линейные перемещения соответствующих точек объекта АВСД в направлениях осей координат О₀X₀ и О₁V₂ , отображаются непосредственно на плоскость x , у изображения видеокамеры. Векторы x _{2 x} , x ^' _{2 x} и x _{3 y} , x 3 y , отображаемые на плоскость изображения видеокамеры, характеризуют перемещения соответствующих точек контролируемого объекта АВСД вследствие его поворота вокруг осей O 1 V 1 и О 2 U 3 на углы а и р . Поскольку параметры L x и L y тестового объекта АВСД известны, то переход от векторов x _{2 x} , x _{2 x} и x _{3 y} , x _{3 y} к углам а и в является тривиальной задачей и не рассматривается.

Приведенное (дважды инвертированное изображение) отображение последовательности соответствующих промежуточных положений ⁽ a o b o c o^до, a₁b₁C₁ ^g ₁ , a 2 b 2^C2^д2, ^а3^Ь3^С3^Д3 , a₄b₄c₄д₄ ) контролируемого объекта АВСД на плоскость изображения камеры показано на рис. 4.

Согласно положениям метода измерения в определенных точках плоскости изображения закрепляются виртуальные метки, связанные с системой координат x , y камеры, относительно которых и определяются результирующие перемещения точек контролируемого объекта. В данном случае метками являются точки M ₁ ,

M ₂ , M ₃ , расположенные на соответствующих координатных осях камеры. В начальный момент времени положение метки M ₁ совпадает с положением точки ао, положение метки M 2 совпадает с положением точки о ₀ , положение метки M ₃ совпадает с положением точки b ₀ .

На рис. 4 показаны также векторы о х ^ _x , о x _{2 x} , о х 2 x , ° x 1 у , ° x 3 у , ст ^х з у , являющиеся изображениями проекций информативных составляющих перемещений соответствующих точек контролируемого объекта. В данном случае, исходя из соображений симметрии, 1 ° ^x 2 x I = ° ^x 2 x I и ° ^x 3 у | = ° ^x 3 у . В общем случае последние равенства могут не выполняться.

В соответствии с (14) запишем систему уравнений:

• Y 1 x = ^{-о ( x} 1 x + ^x 2 x ^);

• Y 2 x = ° ^{( -} L x /2 + ^x 1 x ^);

• Y 3 x =^{- о (} L x + ^xx 1 ^{- x} 2 x )

• Y 4 у =—° ⁽ x 1 у );

Y 5 у = ^{-о (L}y /² + ^x 1 у ^{- x} 3 у ),

где Y 1 x , Y 2 x , Y 3 x , Y 4 у , Y 5 у — изображения многокомпонентных перемещений соответствующих точек контролируемого объекта АВСД, которые записаны в соответствии с представленными в методе формальными моделями.

Они отсчитываются в соответствующий такт измерения от меток M ^, M 2 и M 3 в направлениях, показанных на рис. 4 стрелками; L – приведенная к скалярной модели компонента многомерного теста L .

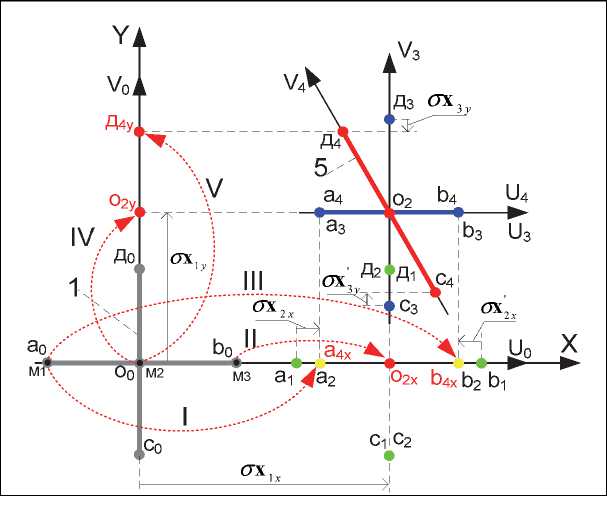
Рис. 4. Дважды инвертированное изображение adcд объекта АВСД, фиксируемое видеокамерой и отображающее последовательность положений изображения контролируемого объекта

В соответствии с (15) определим Якобиан Ja = 274 L для системы уравнений (22):           x. По скольку для оптического преобразователя 7 * 0, а Lx * 0 и Ly * 0 (последние являются известными параметрами многомерного тестового объекта), то Ja = 274Lx * 0, и система уравнений (22) разрешима относительно информативных компонентов x1x , x2x, x1y, x3y .

Решая систему уравнений (22) относительно x _{1 x} , x _{2 x} , x 1 y , x 3 y , получаем измерительновычислительные алгоритмы для определения указанных информативных составляющих сложного перемещения объекта АВСД, которые описаны однородной матрицей композиции преобразований (21) и отображены на графической модели (рис. 3):

₌ _ ^Lx ^{( 2Y} 2 x ^{- Y} 1 x ^{- Y} 3 x )

^x                                    ;

• ¹ x     2 ( 2 Y 2 x + Y i x + Y 3x )

x = L x ( 2 Y 2 x + 3 Y 1 x — Y 3 x ) _;

• ² x    2 ( 2 Y 2 x + Y i x + Y 3 x ) ;

• =     2 Y 4 yL,

• x ¹ y   2 Y 2 x + Y i x + Y 3 x ’

• = L y - 2 L x Y 5 y — Y 4 y )

• x ^{3 y}    2   2 Y 2 x + Y ix + Y 3x '

Данные алгоритмы после программной реализации в структуре измерительной системы завершают процесс создания оптической ИИС для определения информативных составляющих сложных перемещений подвижного объекта, отвечающих модели (3).

Как следует из формального аппарата комбинирования коэффициентов v ius , ^ ijs , ^ tus , ^ ijs и показателей p и q в системе уравнений (14), представленная реализация не единственная. Количество вариантов и их вид определяются в процессе решения конкретной задачи и зависят как от числа информативных компонентов, подлежащих определению, так и от критерия качества, формируемого в процессе постановки решаемой задачи.

Комбинационный аппарат формального синтеза систем уравнений вида (14) для использования в ИИС многокомпонентных физических величин перспективен еще и потому, что позволяет осуществлять автоматизированный поиск множества вариантов, приемлемых как с точки зрения физической реализуемости, так и исходя из потребностей конкретных технических применений.