Математическое моделирование нагрева порошкового композиционного материала в плазменной струе

В.Л. Китайкин2, А.Н. Плотников1

• ¹    Самарский государственный аэрокосмический университет

• ²    ОАО "Металлист", г. Самара

Решена задача Стефана для случая плавления двухслойной композиционной частицы при её транспортировке в плазменной струе струйного плазмотрона. Установлен диапазон параметров, обеспечивающий проплавление плакирующей оболочки и разогрев твёрдого ядра частиц.

В настоящее время ответственные детали любого изделия авиакосмической техники при эксплуатации нуждаются в защите от различного вида воздействий: высоких или низких температур, агрессивных сред и т.д. Как показывает практика, одним из самых перспективных способов их защиты является плазменное напыление. Однако для того чтобы получать стабильные покрытия с заданными физико-механическими свойствами необходимо управлять процессом напыления. В частности необходимо изучить поведение напыляемой частицы в плазменной струе.

Напыляемый материал при нанесении покрытий вводится в плазменную струю, нагревается, ускоряется, деформируется при ударе о напыляемую поверхность детали, растекается и, остывая образует покрытие. Процессы соединения при этом рассматриваются как химическая реакция на поверхности раздела фаз, вступивших в физический контакт в результате деформации и растекания частиц.

Адгезионная и когезионная прочность покрытий определяется развитием химического взаимодействия на межфазной границе. Высокие эксплуатационные свойства покрытий получаются при соблюдении жестких требований к температурному состоянию частиц не только в момент взаимодействия с подложкой, но и на промежуточных этапах нагрева. Как установлено в целом ряде работ при взаимодействии порошкового материала с плазменной струёй происходит изменение фазового состава материала порошка, окисление, диссоциация, взаимодействие с окружающей средой, испарение и т.д. Все эти процессы приобретают особое значение при использовании для напыления композиционных материалов, частицы которых представляют собой систему введенных в контакт и скрепленных между собой различных по составу и природе материалов, например, плакированных порошков [I].

При напылении порошка карбида титана плакированного никелем происходит взаимодействие карбида титана и никеля с образованием двойного титан-никелевого карбида (TiNi)6C и интерметаллидов системы TiNi. Количество этих фаз в покрытии составляет около 10%. Процессы межфазного взаимодействия, происходящие в частицах в процессе нагрева плазменной струёй можно анализировать, изучая частицы порошка, отобранные из струи в процессе напыления. Для состава карбид титана-никель характерно существенное различие в температурах плавления компонентов (3420 К и 1728 К соответственно), в системе титан-никель возможно образование интерметаллидов.

Различия в температурах плавления компонентов плакированной частицы, в поверхностном натяжении и других физико-химических характеристиках приводят к развитию процессов взаимодействия первоначально в системе твердое тело - расплав, а затем между двумя расплавами. В результате нагрева частицы композиционного порошка до стадии плавления хотя бы одного компонента эта система становится неравновесной. При плавлении относительно легкоплавкой оболочки на тугоплавком ядре образующаяся пленка расплава находится под воздействием, с одной стороны, сил адегзии между твердой и жидкой фазами, а с другой сворачивающих усилий, обусловленных силами поверхностного натяжения расплава. Устойчивость расплава плакирующей пленки на ядре частицы композиционного порошка зависит от размера частицы, толщины оболочки и физико-химических свойств системы расплав оболочки - твердое ядро. Защитные свойства плакирующей оболочки и межфазное взаимодействие в процессе напыления имеют место лишь в том случае, когда расплавленная оболочка не уносится плазменным потоком.

Из вышеизложенного можно сделать следующий вывод: плакирование порошковых материалов может существенно уменьшить эффекты разложения и окисления соединений только в том случае, если температура частицы в период нахождения в плазменной струе лежит в определенных пределах. Во-первых, температура частицы не должна быть ниже определенной величины, обеспечивающей интенсивное протекание топохимических реакций взаимодействия порошка с основой. Во-вторых, нагрев плакирующей оболочки до высоких температур может привести к ее испарению или уносу газодинамическим потоком. Возможно также плавление карбидного ядра, которое приводит к чрезмерному развитию процессов межфазного взаимодействия, образованию ин-терметаллидов, охрупчиванию связки, отрицательно влияющих на свойства покрытия. То есть при напылении износостойких покрытий нужно проводить процесс таким образом, чтобы сохранить твердую фазу и мягкую матрицу. Как отмечалось ранее, развитие процессов взаимодействия определяется в первую очередь нагревом и распределением температур в частице. Отсюда следует, что регулирование взаимодействия требует создания методов расчета нагрева частиц в зависимости от основных энергетических параметров струи [1, 2].

Расчетная оценка скорости и температуры частиц представляет сложную задачу, что объясняется непрерывным изменением параметров газа, режима обтекания частицы, теплофизических свойств материала частицы, изменением ее агрегатного состояния в процессе движения в струе.

Рассмотрим сферическую частицу, состоящую из ядра и оболочки с различными теплофизическими свойствами. Частица нагревается через внешнюю поверхность нестационарным тепловым потоком (рис.1). Охлаждение частицы происходит в общем случае в результате конвекции и теплоизлучения.

Величины, относящиеся к ядру частицы, будем писать без индексов, а относящиеся к оболочке - с индексом "I".

В области температур, не превышающих температуру фазового перехода материала частицы, математическая модель нагрева такой системы должна содержать: уравнения теплопроводности для ядра и оболочки, граничные условия на внешней поверхности оболочки, граничные условия на границе ядра и оболочки, граничные условия в центре ядра частицы, начальные условия. Такая модель будет справедлива при нагреве частицы до начала плавления никелевой оболочки и ранее опубликована в ряде наших работ.

При достижении на внешней поверхности частицы r = R 1 температуры равной температуре плавления никеля Т = 1728 К математическая модель нагрева частицы примет следующий вид:

с р 22- = div ( Л gradT ) , ∂ t

при г е [0, 7?];

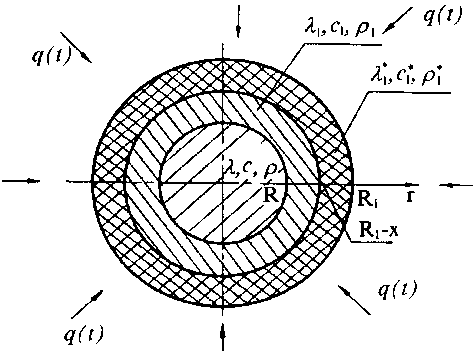
Рис.1. Схема частицы нагреваемой плазменной струей с1 Pi дТ = div (Aj gradTJ ,       (2)

при r e [R, R 1 -x(t)];

^{( ж )}

c ( ^{ж )} p ( ж ) ^d T   = _div ^ ^ж ) gradT ^{ж )} ) , (3)

dt при r e [R1-x(t), R],

твердой фазы. Запишем уравнение теплового баланса для расплавленного слоя плакирующей оболочки

4 n R >T_n - T ) dt =

T ( (R , t) = T ( R , t) ,             (4)

A (

d T y d r

, dT A--

r = R

d r r = R ’

^{( ж} )

1 ( ж ) ^d T 1

¹       d r

r = R ,

r = R i - x ( t )

dx

= Y i P i~A dt

, (6)

A ^{ж )}

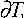
( ^ж )

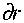
r = R i

d T 1

^A d r

a ^{( ж )}

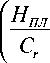
( ж )

T

ш / д⁴

,(7)

r = R i

'    [ R - x ( t ), t ] = T , [ R i - x ( t ), t ] s T™ , (8)

A Д- = 0, T (0, t) < ~ , dr r = 0

T ( r ,0) = T ⁽⁰⁾ ( r) ,         (10)

T ( ( r ,0) = T ( r ) ,         (11)

где (3) - уравнение теплопроводности для жидкого никеля; (6) и (7) - первое и второе условие Стефана для границы плавления никеля (величины, имеющие индекс (ж) относятся к жидкому никелю), X, с, р и X 1 , с 1 и р 1 , - коэффициент теплопроводности, удельная теплоемкость, плотность материала ядра и оболочки соответственно; а коэффициент теплообмена; ^_ПЁ -энтальпия плазменной струи; Cr - эквивалентная теплоемкость; £ -коэффициент черноты поверхности частицы; о - постоянная Стефана-Больцмана; Т_о -начальная температура частицы.

Для упрощения постановки математической модели необходимо решить задачу Стефана для движущейся границы плавления. С учетом малости толщины оболочки пренебрегаем перегревом жидкой фазы, то есть, считаем, что все тепло от потока идет на плавление оболочки и дальнейший нагрев

dT

= 4 п ( R ₁ - x ) ² у₁ р₁ dx + 4 n ( R ₁ - x ) ² A —¹     dt , ⁽¹²⁾

dr r=r1-x где R1 - радиус плакированной частицы; x(t) толщина расплавленного слоя; T^ - температура плазмы; Тпл., а, у, р1, X1 - теплофизические параметры материала оболочки. За начало отсчета времени примем начало процесса плавления T1(R1,0) = Тпл. Введем безразмерные переменные

^ = x^ , Fo = atL , U = -Л¹-- (13)

R i        R²      т n - r_M

и преобразуем (12) к следующему виду

7 Х - S t d U + dFo       d<^

Bi

(1 - ^ )²

= 0 , (14)

где S T = ^{A 1 ( Tn}---^Tпл ) - критерий Сте- Y 1 P 1 ^a 1

aR.

фана, Bi = —⁽. Выражение (14) является ана

логом I условия Стефана (7). Второе условие Стефана (8) (условие постоянства температуры на границе раздела фаз) в координатах ^Fo будет иметь вид

d U    d ^ d U

---+ —---= 0 , d F₀   dF ₀ д^

Подставив (14) в (15) получим

d ^ dFo

+ S_T

или обозначая

V = »L , dFo

d U d Fo

V ² + S_T

Bi   d ^

(1 - ^ )² dFo

d U    Bi

-

_ d Fo (1 - ^ )²

V = 0, ( ¹⁶ )

будем иметь уравнение движения фазовой границы плавления оболочки при начальном условии

V(0) = 0.               (17)

Для системы уравнений (1) - (11) введем безразмерные параметры

Е = r , Е , ( Fo ) = R^ >  1, RR

и (1, Fo )

Н-А

1 + — ( Е 1 ( Fo ) - 1) H

1 Г         1 д и

+ - [ Е 1 ( Fo ) - 1 ]— . и           дЕ

= 0

Е = 1

a 2 1        Т^Т

Fo =-- , U = Е — R

т и 1 = Е -

1 Т

Т

, b ²

пл

-™

-       ’ а2

= Т’ а

. (18)

Таким образом, получили новую краевую

задачу уже с неподвижными границами

А

^X = а

ди _ д 2и дFo = дЕ 2

0 <  Е <  1; 0 <  F о <  F о _ ;

Краевая задача в обозначениях (18) будет выглядеть следующим образом:

и ( Е ,0) = и 0 ( Е ); и (0, Fo ) s 0;

и (1, Fo ) +

£ ( Fo ) д и

X ^{+ (} X ^{- 1} ) ^{£ (} Fo ) ^дЕ е = 1

s 0,

д и d Fo д и _T d Fo

= ^д U 0 <  Е <  1

дЕ ² ’         ^?      '

= b2 ^Ж  1 < E < E1(Fo ), дЕ

и( Е ,0) = Е f^{( Е ) Тпл} = U « е ), ^Т пл

и 1(Е,0) = Е f‘^ Тпл = U 1(0)(Е), (19) Т пл и (0, Fo ) = 0,

U 1 (1, Fo ) s и (1, Fo ),

д и

^Е дЕ ^и

= X

Е = 1

д и ₁ дЕ

^{- и} 1

Е = 1

и Д Е Д Fo ), Fo ] s 0.

(22) где £(Fo) =Е 1 (Fo) - 1.

Функция U(^, Fo) описывает распределение температуры в ядре в период плавления плакирующей оболочки. Таким образом, система уравнений (1) - (11) сведена к существенно более простой задаче, состоящей из системы уравнений (16) -(17), описывающей движение фазовой границы, и системы (22), описывающей этап нагрева и плавления частицы.

Для нахождения в явном виде уравнения движения фазовой границы решим систему (16)-(17).

Продифференцируем (14) по £

Функция Е^Ро) известна из решения уравнения теплового баланса (12). Учитывая малость параметра £ ^0)-1 представим U₁(E₎,Fо) в виде ряда по ^-1 в точке ^=1, ограничиваясь линейным членом

dv д 2и    2 Bi dE    T[ дЕ2 + (1 -Е)2.

Используя уравнение теплопроводнос

ти для шара

и 1 ( Е , Fo ) = и 1 (1, Fo ) + ( Е - 1) ^{д и}. ^дЕ

. (20)

Е = 1

ди _ 1 д ²[ и (1 - Е )]

<7" 1- Е   Ер ■    ⁽²⁴⁾

и второе условие Стефана, получим

Используя граничные условия в точке ^=/, преобразуем (20) к следующему виду:

и 1 ( Е , Fo ) = и (1, Fo ) +

+ ( Е - М

^ -^ и (1, Fo ) + X

1 д и

X дЕ

д ² и   д и    2     д и

— =--1----- дЕ2   efo (1 - E)V efo ди f,     2 )

=     1 + efo ( (1 - E)V J

Е = 1

Полагая в (20) ^=^ (Fo), получим граничное условие для функции U(E,Fo) в точке ^=1

Подставляя (25) в (23) получим:

dv dE   T

Г ^ и f 1 +       )

EFo

( (1 - E ) v J

2 Bi

⁺ (1 - E )³ .

Выразим из (16) --- и подставим в dFo dU _ 1 тл2 STBiV V dFo     ST [     (1 -Е)2

C —

- S_TBi e^T

•

STBi

Окончательно получаем зависимость скорости движения границы от координаты Е в следующем виде dV _ ТЛ2  STBiV

V d^     [      (1 - ^)2

2 S _T Bi

+ (1 - Е )3

или

1 +

(1 - ^ ) V

+ (27)

V ( Е )

S _T Bi ------- +

(‘ - Е )²

exp

S _T Bi ‘ е

dV . V ( S_TBi   A 4 S_TBi

+ v ^{2 T} 2

d^         1 - Е [ 1 - Е J (1 - Е)3

Е

J ^exP

о

^ST^Bi 1 d _T - ^exP [^{- S}T^Bi ] 1 - т J S T Bi

Получили уравнение Риккати. Частное решение (28) имеет вид

Зависимость E(Fo) получаем в виде обратной функции

Е

F 0 — J

dt

V xo •

V Е ) — S T Bi

‘^    (1 - Е ) ² '

Сделаем замену переменных

1     S T Bi

V — —। w (1 -Е)2.

Получаем относительно неизвестной функции W(E) линейное уравнение

Краевую задачу (22) решаем методом преобразования Фурье. Краевая задача формально совпадает с краевой задачей III рода для пластины с коэффициентом теплопередачи, зависящим от времени. Решение (22) будем строить методом конечных элементов. В качестве элементов возьмем разбиение временного интервала Fo е [0; Fo1] и аппроксимируем на данном разбиении зависимость dW W _ STBi аЕ 1-Е Г +1^1

Общий интеграл уравнения (29) имеет вид:

W ( Е ) — exp

STBi

If Е a exp

^J 0

STBi

1 - т

dT + C

e (Fo)

X + X - 1) e Fo простой функцией

e ( Fo ) — e i , Fo ⁽ i ^{- 1)} <  Fo <  Fo ⁽ i ) , i — 1 m . (33) Тогда краевая задача (22) преобразуется в последовательность краевых задач

Возвращаясь к переменной Vполучаем:

d U E — дЩ о <  Е <  1

d Fo       дЕ ² ,      ^?     ,

V ( Е ) —

STBi

(‘ - Е )²

exp

+

ST Bi

1 - Е

Fo ⁽ i ^{- 1)} <  Fo <  Fo ⁽ i ) , i — 1, m ,

U ⁽ i ) ( Е , Fo ⁽ i ) ) — U ⁽ i ^{- 1)} ( Е , Fo ⁽ i ) ),              ⁽³⁴⁾

Е

J ^exP о

ST Bi

1 - т

. (31)

U ⁽ i ) (0, Fo ) = 0;

d T + C

U ⁽ i ) (0, Fo ) +

e i          d U ⁽ i )

X ^{+ (} X ^{- 1) e} i ^дЕ _{Е —} 1

= 0

Константу С определяем из начальных условий, откуда следует, что

Решение (34) при фиксированном (e)

совпадает с решением задачи III рода для пластины

U ⁽М Fo ) =

^                         Г                         1

= _X A n' ) sint ^ n* 4 )exp[ - P n' ⁾² ( Fo - Fo‘ ^-1) )]’ ⁽³⁵^ n = 1

где pnNi. n = 1, 2, 3, ... - корни характеристического уравнения

tg Цп^ +

E t

X + ( X — 1 ) Ei

цУ = о. (36)

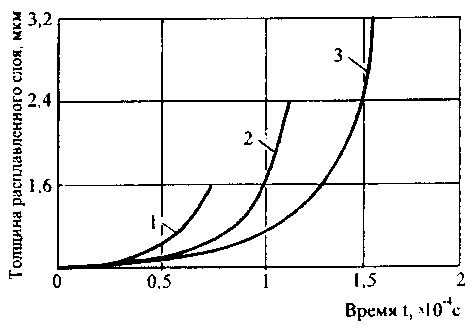
Рис. 2. Зависимость толщины расплавленного слоя от времени нагрева частиц: 1 - частица диаметром 40мкм,2-60мкм, 3-80мкм

Коэффициенты в разложении (35) определяются следующей формулой

J U^M1( _S , Fo ⁽ ' - ¹⁾)sin( p n i ) d ;

A nt = '---------1----------------------

1 ^- J cos(2 p n‘\') d i

,(37)

подставляя (37) в (35) получаем следующее рекуррентное соотношение га              1

U ^{( t )} ( Ч Fo ) = X — / U ^{( t - 1)} ( i , Fo ^{( t - 1)} ) sin( pn^) X n = 1 ^ n

X sin( p n' i exp ] - p n^{t )2} ( Fo - Fo ^{( t - 1)} ) ]

где обозначено

a

( t ) = 1

ⁿ 2

1 - J cos(2 p ni ⁾ i ) d i

Полученная рекуррентная последовательность функции и(^,Еа), i=1, m позволяет рассчитать распределение температур в плакированной частице в период плавления плакирующей оболочки.

Результаты теоретического расчета распределения температур в плакированных частицах карбида титана приведены на рис.2 и 3. Расчет проведен для режима напыления: расход аргона - 2,6 м3/ч, расход водорода - 0,5 м3/ч, ток дуги - 380 А. Проведенные исследования показали, что этому режиму напыления соответствуют: температура в ядре плазменной струи Тпл=11300 К, коэффициент теплопроводности плазмы в ядре кИС 0,57 Вт/ м-К, скорость струи Уп=828 м/с, коэффициент вязкости ц, =1,98-10-4 кг/с-м. Теплофизи- ческие параметры никелевой оболочки следующие: р1=8,96-103 кг/м3, Х1=60 Вт/м-К, C 1=550 Дж/кг- -К. Теплофизические параметры карбида титана-хрома: р=4,92-103 кг/м3, Х=6 Вт/м-К, с=894 Дж/кг-К.

Расчеты проводились для частиц диаметром 40, 60, 80 мкм и показали, что распределение температур в напыляемых частицах зависит от их диаметра. Перепад температур в центре и на поверхности ядра частицы в момент начала плавления оболочки достигает 400 К. Длительность плавления никелевой оболочки изменяется от 0,075-10-3 с до 0,154-10-3 с (табл.), зависимость толщины расплавленного слоя никеля во времени нагрева частиц представлена на рис.2. Следует отметить, что толщина никелевого слоя при плакировании 30% мае. Ni для частиц диаметром 40 мкм составляет 1,6 мкм, для час-

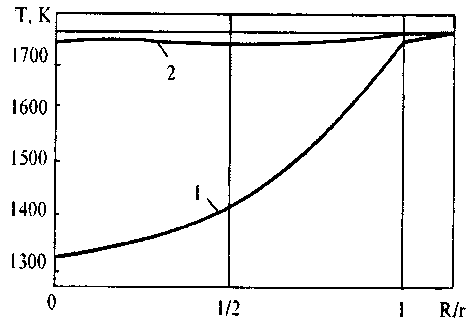
Рис. 3. Распределение температуры по сечению карбидного ядра в частице диаметром 60 мкм в начальный момент плавления оболочки (1) и в момент ее завершения (2)

Таблица. Длительность нагрева частиц при движении на высокотемпературном участке струи

Диаметр частицы, мкм	Время нагрева до Тпл, с	Время плавления оболочки, с	Суммарное время, с	Время полета в высокотемпературной зоне, с
40	0,168 ⋅ 10-3	0,075 ⋅ 10-3	0,243 ⋅ 10-3	0,3 ⋅ 10-3
60	0,377 ⋅ 10-3	0,114 ⋅ 10-3	0,491 ⋅ 10-3	0,5 ⋅ 10-3
80	0,667 ⋅ 10-3	0,154 ⋅ 10-3	0,821 ⋅ 10-3	0,7 ⋅ 10-3

тиц диаметром 60 мкм - 2,4 мкм, для частиц 80 мкм - 3,2 мкм.

Для определения степени расплавления частиц необходимо определить время их полета в высокотемпературной зоне струи. Длина ядра струи при напылении соплом диаметром d=6 мм составляет приблизительно 12 мм (2d). Поскольку ввод частиц порошка осуществляется на расстоянии 4 мм от среза сопла, длина высокотемпературного участка струи, в котором нагрев частиц наиболее эффективен составляет 16 мм. Учитывая, что скорость частиц в плазменном потоке определяется их массой и размером, рассчитывалось время, в течении которого частица пролетит высокотемпературную зону (табл.). Анализ результатов расчета позволяет сделать вывод о степени проплавления частиц за время их движения на высокотемпературном участке струи.

Металлографические исследования степени расплавления частиц, отобранных в процессе напыления подтверждают адекватность разработанной модели.