Математическое моделирование напряженно-деформированного состояния цилиндрической оболочки мембранного покрытия с подкрепляющим элементом

На сегодняшний момент развитие строительства большепролетных мембранных покрытий остается актуальным в связи со значительным числом возводимых объектов спортивного, социально-культурного и общественного назначения [1-4]. Ввиду этого вопрос надежности проектируемых конструкций, а в особенности мембранно- го покрытия, включающегося в совместную работу при поперечном изгибе с подкрепляющими элементами постели, остаётся актуальным. Проектируемые сегодня конструкции отличаются значительным разнообразием геометрии поверхности: плоские, положительной, отрицательной, нулевой гауссовой кривизны, первоначально плоские или с заданной стрелой провисания и т. п. Одной из осо- бенностей работы таких конструкций является не в полной мере исследованный вопрос в части совместного взаимодействия тонкостенной мембранной оболочки и подкрепляющего элемента конструкции под действием поперечной нагрузки. Теоретические исследования и внедрение конструктивных решений для большепролетных мембранных конструкций изложены в работах [5–8].

С учётом исследований [9, 10] закономерности изменения напряжений, возникающие в тонколистовой мембране и подкрепляющем элементе жёсткости под действием поперечной нагрузки, определяются коэффициентами k ₁ , k ₂ , k ₃ , которые характеризуют степень влияния подкрепляющего элемента на его совместную работу с мембранной оболочкой. В результате были получены экспериментальные данные, представленные в [11]. При этом возникает задача анализа, оптимизации и обобщения полученных экспериментальных данных для последующей разработки методики расчёта напряжённо-деформированного состояния тонкостенных оболочек с различной кривизной поверхности.

Постановка задачи. Разработать математические модели для коэффициентов k i = f ( x 1 , x 2 ) , характеризующих напряженно-деформированное состояние мембранных покрытий с различной кривизной поверхности, где x ₁ – функция жестко-стных характеристик, а x ₂ – кривизна поверхности тонкостенной оболочки.

Метод

Базовыми инструментами математического моделирования для обработки и анализа экспериментальных данных являются интерполяция и аппроксимация. При этом наибольшее распространение в инженерной практике получил аппроксимационный метод наименьших квадратов [12–14], который лежит в основе регрессионного анализа и заключается в минимизации суммы квадратичных отклонений между исходными данными и расчётными:

n

E ( z i - z i ) ^ min.

i = 1

где z_i – исходные значения экспериментальных данных; z_i – расчётные значения, полученные в результате аппроксимации.

В соответствии с методом наименьших квадратов минимизация целевой функции в виде сум- n ₂ мы квадратов регрессионных остатков ^ ( z i - z i ) i = 1

происходит методами математического анализа. В общем случае задача минимизации решается методом математического анализа функции многих переменных, который подразумевает определение частных производных с последующим со- ставлением и решением системы алгебраических уравнений. Однако, как следует из того же математического анализа, в случае с функцией многих переменных исследование на экстремумы (в нашем случае – минимум) необходимо проводить не только внутри, но и с учётом границ исследуемой области, что в значительной степени усложняет как математическое описание, так и программную реализацию такого решения. Исходя из этого в работе предлагается использовать быстродействующие численные алгоритмы поиска экстремальных значений, реализованные в программном пакете MS Excel в виде функции «Поиск решения», по аналогии с [15].

Традиционно критерием адекватности полученных моделей, свидетельствующих о степени их соответствия исходным экспериментальным данным, служит коэффициент детерминации R ² , который определяется следующей зависимостью:

n

Z i zi ^{- z} i )

R2 = 1 - -i=i-----------, n Яzi -z)2 i=1

где z – среднеарифметическое значение исходных экспериментальных данных.

Коэффициент детерминации R ² для модели принимает значения от 0 до 1. Считается, что чем ближе значение R ² к 1, тем сильнее зависимость, а при R ² = 1 достигается функциональная зависимость между аппроксимирующей функцией и исходными данными.

Тогда получается, что максимальное значение коэффициента детерминации R ² на интервале от 0 до 1 достигается при минимальных значениях суммы квадратов регрессионных остатков ⁿ

^(zi - zi) . Исходя из вышеизложенного, пред- i=1

лагается в качестве целевой функции использовать непосредственно коэффициент детерминации R ² , но находить при этом его максимум с помощью функции «Поиск решения» на интервале значений от 0 до 1.

Для первых двух функций k = f ( x^ x 2 ) и к 2 = f 2 ( X 1 , x 2 ) используются исходные данные непосредственно из таблицы. Чтобы увеличить точность итоговой модели по отношению к исходным данным, применительно к факторам x ₁ и x ₂ , определяющих функцию к 3 = f₃ ( x 1 ,x 2 ) , было использовано нормирование, т. е. каждое отдельное значение было поделено на максимальное. В результате получим следующие значения факторов для построения модели к ₃ = f₃ ( x 1 , x 2 ) (см. таблицу).

Конопацкий Е.В., Шпиньков В.А., Бездитный А.А.

Обратное вычисление натуральных значений формул:

Нормированные значения факторов для построения модели к 3 = f 3 ( x 1 ,x 2 )

х1 х2 Натуральные значения фактора Нормированные значения фактора Натуральные значения фактора Нормированные значения фактора 8,89 1,00 0 0 1,11 0,13 0,008 0,259 0,33 0,04 0,011 0,345 – – 0,016 0,515 — — 0,032 1 факторов осуществляется с помощью следующих

x x2H

Xo ~ , ²  0,032

x = H , ¹   8,89

где x _{1 H} и x _{2 H} – нормированные значения факторов x ₁ и x ₂ .

В результате проведения вычислительных экспериментов были подобраны следующие аппроксимирующие функции, обеспечивающие высокие значения коэффициента детерминации:

k 1 = a 1 x 2 x 2 + b 1 x 2 + c 1 x 1 x 2 + d 1 x 1 + e 1 x 2 + f 1 , к 2 = a 2 x 2 + b 2 x 1 x 2 + c 2 x 1 + d 2 x 2 + e 2 ,

6   65   54   4

k 3 = a 3 ^x 2 H^x1 H + b 3 ^x 2 H + c 3 x 2 H^x1 H ⁺ d 3 ^x 2 H ^{+ e} 3 ^x 2 H^x1 H ⁺ f 3 ^x 2 H ^{+ +} g 3 ^x 2 H^x 1 H ⁺ h 3 ^x 2 H ⁺ i 3 ^x 2 H^x1 H ⁺ j 3 ^x 2 H ^{+ k} 3 ^x 1 H^x 2 H ⁺ l 3 ^x 2 H ⁺ m 3 ^.

Для реализации метода наименьших квадратов были использованы возможности табличного процессора MS Excel. При этом с помощью команды «Поиск решения» были найдены значения полиномиальных коэффициентов, обеспечивающие для каждой модели максимальные значения коэффициента детерминации на интервале от 0 до 1.

В результате получены следующие математические модели в виде полиномиальных зависимостей:

k 1 = 2,55 x 2 x ₂ - 0,046 x 2 + 3,057 x , x ₂ + 0,801 x , + 2,925 x ₂ + 0,789;

к ₂ = 0,058 x 2 - 0,009 x , x ₂ - 0,633 x , + 0,02 x ₂ + 1,502;

к ₃ = 258,033 x 6 _H x 1 _H + 546,743 x 6 _H - 3,064 x 5 _H x 1 _H - 0,754 x 5 _H -

- 260,239 x 4 _H x 1 _H - 543,407 x 4 _H - 258,591 x 3 _H x 1 _H - 551,504 x 3 _H +

+ 340,309 x 2 H x ! _H + 686,824 x | _H - 74,744 x j _H x _{2 H} - 107,228 x _{2 H} + 6,672.

Для всех трёх моделей коэффициенты детерминации варьируются в пределах R ² = 0,997...0,999 .

n ₂

Поскольку общая дисперсия Е ( z i ^- z ) является величиной постоянной, аналогичный результат i = 1

можно получить, если минимизировать непосредственно сумму квадратов регрессионных остатков

n

^(zt -:;.) . Однако в этом случае решение нужно искать на всём интервале значений, который для каж- i=1

дой отдельной функции будет различным. Поэтому предпочтительней использовать коэффициент детерминации R ², значения которого всегда находятся в интервале от 0 до 1.

Результаты и обсуждения

Полученные в результате моделирования коэффициенты детерминации говорят об очень высокой достоверности математических моделей. Однако чтобы убедиться в этом наглядно, выполним графическую визуализацию полученных моделей (рис. 1).

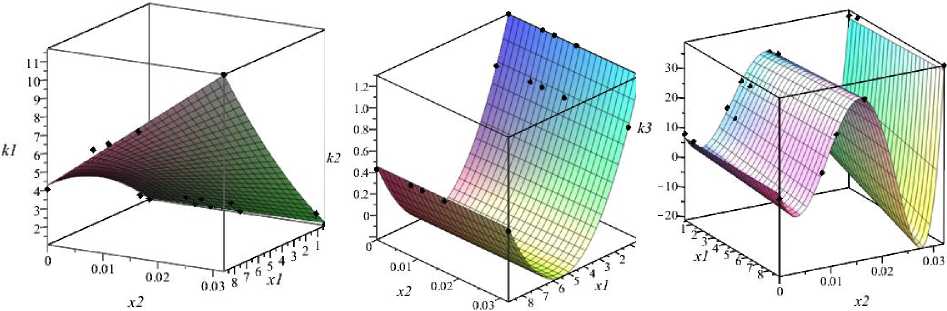
Рис. 1. Графическая визуализация математических моделей, полученных с помощью двумерной аппроксимации

Визуализация первой модели подтверждает достоверность модели по отношению к исходным данным. А вторая и третья модели, как видно из рис. 1, несмотря на высокие значения коэффициента детерминации, склонны к незапланированным осцилляциям, которые никак нельзя обосновать, исходя из условий протекания исследуемого процесса. В частности, коэффициенты k ₂ и k ₃ не могут быть отрицательными. Исходя из этого, для второй и третьей модели необходим поиск других решений.

Эту же задачу можно решить с использованием геометрической теории многомерной интерполяции [16–19], которая предусматривает использование геометрических интерполянтов для моделирования многофакторных процессов и явлений. Под геометрическим интерполянтом понимается геометрический

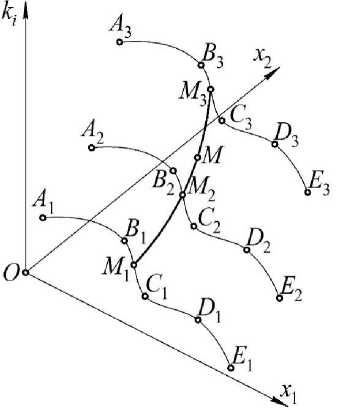
Рис. 2. Геометрическая схема моделирования напряженно-деформированного состояния цилиндрических оболочек мембранных покрытий с помощью двумерной интерполяции

объект, проходящий через наперёд заданные точки [20], координаты которых соответствуют исходным экспериментальным данным. Для построения геометрических интерполянтов необходимо разработать геометрическую схему и описать её аналитически с помощью дуг кривых, проходящих через наперёд заданные точки. Аналитическое описание геометрических интерполянтов выполняется с помощью математического аппарата «Точечное исчисление» [21–23].

Геометрическая схема моделирования напряженно-деформированного состояния цилиндрических оболочек мембранных покрытий с подкрепляющим элементом (рис. 2) представляет собой геометрический алгоритм построения поверхности отклика, проходящей через 15 наперёд заданных точек. Он включает определение опорных линий A1B1C1D1E1 , A2 B2C2 D2 E2 , A3B3C3D3E3 и обра зующей линии M1M2M3 геометрического интер-полянта.

На основании геометрической схемы (см. рис. 2) разработан вычислительный алгоритм аналитического определения искомой поверхности отклика, который включает 3 однотипных точечных уравнения для определения каждой из направляющих линий:

M j

= A j

-4   13- 3     13- 2 2  - 3 |      (     3     64- 2 2

u--u u +— u u — uu + B 16 u u--u u

33      J ^jV    з

16    3 )

+ uu +

3 J

+ C j ( — 12 uu + 40 u u^ — 12 uu ^) + D j (-^- u^;

I 64 -2 23 i .

u--u u +16uu+

I -3   , 13-22

+E — u u +—uu j I

—

13- 3 ,4

—uu+

где u - текущий параметр точечного уравнения, который изменяется от 0 до 1; u = 1 — u - дополнение параметра u до 1; 1 <  j <  3.

Конопацкий Е.В., Шпиньков В.А., Бездитный А.А.

Далее следует определение образующей линии поверхности отклика:

M = v (v -0,15v)M1 + 8,842vvM2 + v(v-6,692v)M3, где v – текущий параметр точечного уравнения, который изменяется от 0 до 1;

v = 1 - v - дополнение параметра v до 1.

Обратим внимание, что разработанная геометрическая схема и полученный на её основе вычислительный алгоритм являются одинаковыми для всех трёх моделей k , k и k , но с разными исходными данными. Это даёт возможность посредством покоординатного расчёта получить 3 отдельные модели, которые аналитически определяются с помощью 3 различных систем параметрических уравнений. Чтобы не перегружать статью, приведём систему параметрических уравнений только для первой модели:

% ! = 2,927 v ² - 11,492 v + 8,894

x ₂ = - 0,006 u ⁴ + 0,096 u ³ - 0,113 u ² + 0,056 u

< k 1 = ( 16,278 v ² - 16,492 v - 1,067 ) u ⁴ + ( - 15,863 v ² - 9,31 v + 28,373 ) u ³ + + ( 1,267 v ² + 33,066 v - 37,213 ) u ² + ( 3,582 v ² - 20,109 v + 17,547 ) u -- 0,231 v ² - 2,799 v + 4,06.

Выполним визуализацию геометрических моделей для сравнения интерполяционных моделей с аппроксимационными (рис. 3).

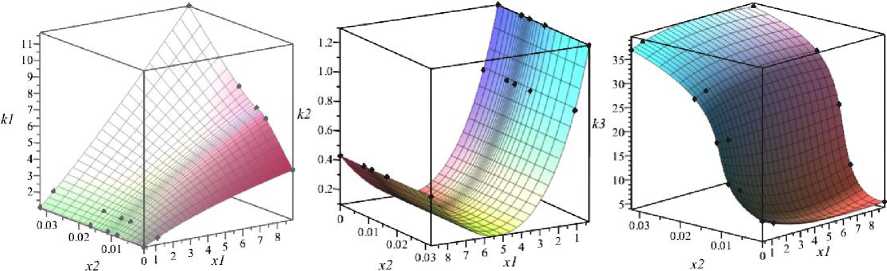
Рис. 3. Визуализация геометрических моделей, полученных с помощью двумерной интерполяции

Из рис. 3 видно, что в данном конкретном случае модели, полученные на основе геометрической теории многомерной интерполяции, наиболее точно отображают характер протекания процесса и потому являются более предпочтительными по отношению к моделям, полученным с помощью двумерной аппроксимации. Вместе с тем аппроксимационные модели получены в виде функций, заданных в явном виде, в то время как интерполяционные модели, полученные на основе точечных уравнений и вычислительных алгоритмов на их основе, представлены в параметрическом виде, что затрудняет их дальнейшее использование в инженерной практике.

Выводы

Описанный в работе подход по реализации метода наименьших квадратов с помощью поиска решений в табличном процессоре MS Excel является в достаточной степени гибким и эффективным инструментом. Его преимуществами являются простота реализации, возможность использования натуральных значений факторов и возможность обобщения на многомерное пространство, что расширяет существующий инструментарий моделирования многофакторных процессов и явлений. Но также он обладает недостатками, присущими классическому методу наименьших квадратов в части возникновения незапланированных осцилляций между узловыми точками аппроксимации. Поэтому в работе для конкретных моделей реализована двумерная интерполяция на основе геометрической теории многомерной интерполяции, которая показала более качественные результаты не только по отношению к исходным данным, но и по отношению к характеру протекания процесса, что позволило избежать незапланированных осцилляций, которые были ярко выражены на аппроксимационных моделях напряженно-деформированного состояния цилиндрических оболочек мембранных покрытий с подкрепляющим элементом.