Математическое моделирование напряженно-деформированного состояния в поверхностно упрочненных втулках с учетом остаточных касательных напряжений

ВЕСТНИК ПНИПУ. МЕХАНИКА № 1, 2019PNRPU MECHANICS BULLETIN

Материалоемкость, технологическая база производства деталей и элементов конструкций, обеспечение их ресурса – основные задачи современного машиностроения в различных областях промышленности. Поскольку при изготовлении деталей и в процессе их эксплуатации наибольшую «поврежденность» испытывает материал приповерхностного слоя, то уже в течение многих десятилетий используют технологические способы увеличения «сопротивляемости» деталей, эксплуатирующихся при ужесточенных температурно-силовых нагрузках. Одним из самых распространенных технологических приемов является поверхностно пластическое упрочнение (поверхностно пластическое деформирование – ППД) деталей. Создание локальных очагов пластической деформации в тонком поверхностном слое при квазистатическом или динамическом взаимодействии ударного инструмента с деталью при «холодной» обработке ее поверхности или в условиях высоких температур при воздействии мощного температурного потока приводит к появлению в поверхностном слое полей сжимающих остаточных напряжений, с которыми и связывается повышение ресурса, в частности характеристик сопротивления усталости, износостойкости, микротвердости, прочности и других показателей надежности. Число публикаций в области исследования «благоприятного» влияния остаточных напряжений на отмеченные механические характеристики необозримо, отметим, например, работы [1–11]. Арсенал технологий упрочнения достаточно широк. Используются как «классические» методы динамического или квазистати-ческого контакта детали с элементом упрочнения (гидро- и пневмодробеструйная обработка [10, 12–15], обкатка роликом и алмазное выглаживание [10, 13, 15–17], ультразвуковое (механическое) упрочнение дробью с малой амплитудой и высокой частотой до 104 -105 Гц в специальных контейнерах [11, 13, 18–24], дорнование и другие технологии), так и методы термопластического упрочнения [11]. В некоторых случаях используют гибридные технологии упрочнения, например дробеструйную обработку и обкатку роликом в комбинации с ультразвуком [25, 26]. В последнее время широкое применение находят упрочняющие технологии кавитационного характера [27, 28], наиболее интенсивно развивается технология лазерного упрочнения (лазерного удара) [29–32]. Упрочнение лучом лазера повышает, например, предел выносливости образцов, имитирующих кромки лопаток компрессора газотурбинного двигателя (ГТД), на 30–50 %, а стойкость обработанных лазером лопаток повышается вдвое [31]. Как отмечается в публикациях [31, 32], этот метод имеет три основных преимущества перед «классическими» методами упрочнения на основе контактного взаимодействия: более глубокое распространение области остаточных напряжений сжатия; малая степень холодной пластической деформации поверхности, что обеспечивает повышенную стойкость наведенных напряжений сжатия к релаксации при рабочих температурах и вибрации, например, лопаток компрессора ГТД; сохраняется исходным или повышается качество поверхности по степени шероховатости.

Одной из теоретических проблем механики упрочненных конструкций является реконструкция напряженно-деформированного состояния после процедуры упрочнения, поскольку без этой информации невозможно построить математические модели релаксации остаточных напряжений в упрочненных деталях в условиях высокотемпературной ползучести и усталостной прочности при многоцикловом нагружении в поле рабочих нагрузок. Отметим некоторые теоретические исследования в этом направлении. Так, в работах [33–35] сделана попытка оценить распределение остаточных напряжений при единичном ударе шара о плоскость на основе решения контактной упругопластической задачи. Публикации [33–38] посвящены непосредственному моделированию технологических процессов упрочнения для определения остаточных напряжений на основе динамических упругопластических задач; в [11] предложен численный метод расчета полей остаточных напряжений и деформаций, возникающих в процессе термопластического упрочнения (ТПУ), решением соответствующей прямой термоупругопластической задачи. Однако учесть все нюансы упрочняющих технологий (стохастический характер бомбардировки микрошариками, многократные проходы при упрочнении роликом, система охлаждающей жидкости, температурные эффекты в контактной задаче, граничные и начальные условия при ТПУ и т.д.) практически невозможно. Поэтому получаемые результаты носят преимущественно качественный характер. Другое направление теоретических исследований основано на волевом задании закона распределения пластической деформации по пространственным координатам в тонком поверхностном слое (равномерное распределение, линейный или параболический законы по глубине слоя и т.д.). Для некоторых простейших законов в [12] получены аналитические решения для гладких цилиндрических и плоских образ- цов. Этот метод расчета остаточных напряжений по заданным первоначальным деформациям получил развитие в ряде работ [9, 10, 39–41], где использована аналогия между остаточными пластическими деформациями и температурными деформациями в неоднородном температурном поле. Использование этой аналогии дает широкие возможности сведения рассмотренных задач к проблеме термоупругости, реализация которой в современных расчетных комплексах не вызывает особых затруднений. Но здесь приходится вести речь лишь о качественном характере теоретических результатов и получаемых полей остаточных напряжений.

В связи с вышеизложенным для получения более надежных количественных результатов необходим какой-то минимум экспериментальной информации о некоторых компонентах тензора остаточных напряжений (определить распределение остаточных пластических деформаций по глубине упрочненного слоя экспериментально невозможно), зная которые можно расчетным путем определить и остальные компоненты тензора напряжений и тензора пластических деформаций. В этом плане можно отметить работы [39, 40], в которых задача сведена к задаче фиктивной термоупругости. Здесь сделана успешная попытка использовать информацию о раcпределении одной или двух компонент тензора остаточных напряжений, определенных экспериментально. Для этой цели «подбирается» (численно, итерационным методом) такое температурное поле, что температурные деформации, вызванные неоднородным температурным полем, дают (в соответствующей норме) наиболее близкое теоретическое распределение компонент остаточных напряжений к экспериментально определенным.

В настоящей работе в качестве основного подхода для дальнейших исследований используется феноменологический подход, предложенный для цилиндрических изделий в [42] и получивший дальнейшее развитие, в том числе – и для плоских деталей, в работах [15–17, 24, 40]. Суть подхода заключается в том, что не учитываются касательные напряжения, а для определения нормальных компонент тензора остаточных напряжений и пластических деформаций достаточно иметь одну или две (в зависимости от технологии упрочнения) экспериментальные эпюры остаточных напряжений. Естественным развитием данного метода является его обобщение на случай учета касательных компонент тензора остаточных напряжений, которые гарантированно возникают, например, при обкатке роликом, алмазном выглаживании и дорновании.

Поэтому целью данной работы является экспериментальное исследование остаточных касательных и нормальных напряжений после упрочнения алмазным выглаживанием втулок из стали ЭИ961 (13Х11Н2В2МФ), количественная оценка касательных напряжений и разработка математической модели ре- конструкции полей остаточных напряжений и пластических деформаций для рассматриваемой задачи.

1. Предварительные сведения

Во многих прикладных задачах для цилиндрических деталей (поверхностное пластическое деформирование, точение, стесненное кручение и др.) формирование остаточных напряжений одинаково во всех сечениях и в цилиндрической системе координат ( r , θ , z ) не зависит от координат θ и z , т.е. все компоненты тензора остаточных напряжений зависят лишь от радиуса: ст, = ст, ( r ) , СТ_е=СТ_е ⁽ r ) ,      ^ст _z =^ст _z ⁽ r ) ,      ^т r ₈=^Т r ₈ ⁽ г ) , ^т rz =^т rz ⁽ r ) ,

T8z = т8z (r) . Тогда, записывая уравнения равновесия дстr +1дтrе , дтrz , стr-сте : 0 дr   r де    дz      r’ дт 1 дт,, дст т rz +--^ + —z + -r^ = 0,

∂r   r ∂θ   ∂zr дт r е +1 дсте , дтеz । 2тrе = 0

∂r   r ∂θ   ∂zr и учитывая, что компоненты тензора напряжений зависят лишь от одной переменной r , получим

"       '         ■0, drr diт rz + -z = 0,(1)

dr r

• ^dтrе , ^2тrе₌₀

2.    Экспериментальное исследование остаточных напряжений после алмазного выглаживания

drr

Интегрирование второго и третьего уравнений (1) дает t,z = A / r , т_г8 = B / r ², где A и B - произвольные константы. Возвращаясь к задаче поверхностного пластического упрочнения втулки, при котором ее наружная и внешняя боковые поверхности свободны от внешних нагрузок, имеем A = B = 0 и т_гг = т_г8 = 0 . Таким образом, в данной задаче подлежат определению лишь компоненты тензора напряжений ст_г ( r ), ст₈ ( r ), ст₂ ( r ) и т_8z ( r ), при этом ст_г и ст₀ связаны первым соотношением (1), а на σ и τ накладываются ограничения, связанные с гипотезами плоских сечений и прямых радиусов. Кроме этого, должны выполняться условия

R2

J rстz (r)dr = 0 , j r2теz (r)dr = 0,(2)

R, поскольку внешние растягивающая осевая сила и крутящий момент отсутствуют ( R и R – внутренний и наружный радиусы втулки).

Для исследования остаточных напряжений после алмазного выглаживания, которое является штатной технологией в различных отраслях промышленности, использовались    втулки    из    стали    ЭИ961

(13Х11Н2В2МФ) следующих размеров: длина втулки l = 75 мм; наружный диаметр D₂ = 51,5 мм; внутренний диаметр D_x = 45 мм; усилие прижима (радиальное усилие) алмазного наконечника 200 и 300 Н; линейная скорость точек внешней поверхности при вращении втулки 50 м/мин; осевая линейная скорость алмазного наконечника 0,075 мм/об; радиус сферического алмазного наконечника 2 мм.

Принципиальная схема упрочнения и ее техническая реализация изложены еще в работе [46]. Экспериментальное (точнее – расчетно-экспериментальное) определение распределения остаточных напряжений в поверхностно упрочненных втулках осуществлялось по методу колец и полосок С.И. Иванова, основы которого заложены в работах [43–45], широко используемому и в настоящее время [9, 10, 15–17, 24]. Для каждого режима нагружения (усилия прижима) использовалось по 5 втулок, две из которых – для изготовления колец, а три – для полосок (вдоль образующей), которые вырезались в пределах центрального угла у = 26 ° поперечного кольцевого сечения образца.

Из представленного в подразд. 1 материала следует, что при принятых гипотезах формирование остаточных напряжений σ , σ , σ и τ идет независимо, поскольку диагональные элементы тензора деформаций ε , ε и ε влияют только на величины σ , σ и σ , а на сдвиговые деформации они не оказывают влияния. Аналогично внутренний крутящий момент в элементе объема оказывает влияние лишь на сдвиговую деформацию, не оказывая влияния на компоненты ε , ε и ε . Метод колец и полосок позволяет экспериментально определить компоненты ст₀ и ст₂ , а также величину т_8z. Но в связи с вышеизложенным этот метод позволяет независимо определять компоненты σ и σ по линейным перемещениям полоски (балки) и угловым перемещениям (изменениям диаметра) разрезанного кольца соответственно, условно считая т_8г = 0, а величину

τ – по линейному осевому смещению берегов разреза кольца относительно друг друга.

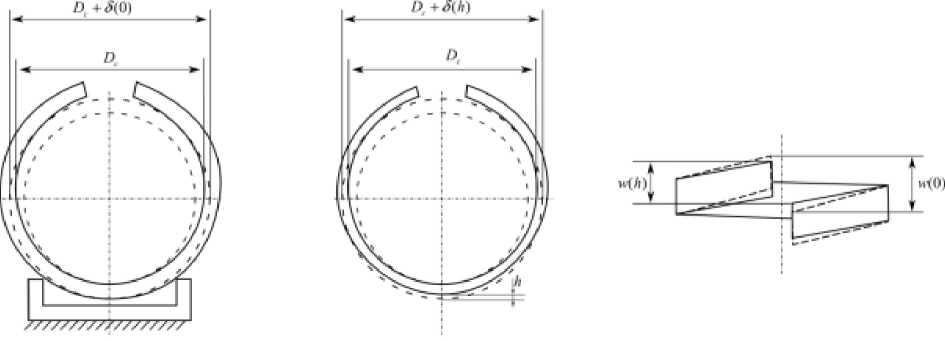
Сразу после вырезки у полосок измеряли прогиб f ( 0 ) (как показано на рис. 1, a ), а у колец - изменение диаметра 6 (0) (рис. 2, a ) и величину осевого смещения w (0) берегов разрезанного кольца (рис. 2, б) . Далее электрохимическим полированием (состав электролита: ортофосфорная кислота – 65 %, серная кислота – 20 %, дистиллированная вода – 15 %) производилось удаление слоев со стороны упрочнения (остальные части поверхности защищались лаком). Послойное травление

(5-10 мкм) приводило к изменению диаметра 5(h) в кольцах (см. рис. 2, б) и прогибов полосок f (h), где h – расстояние от наружной поверхности втулки до слоя, в котором вычисляли остаточное напряжение. Отметим, что f (h) и 5(h) отсчитываются от состояния полоски или кольца до вырезки из втулки. На рис. 1 и 2 полоска и кольцо до вырезки из втулки изображены штриховыми линиями. Толщина удаленного слоя измерялась в 10–15 точках, а результаты измерений усреднялись. Детали этой методики подробно изложены в работе [9].

б

Рис. 1. Схема измерения прогиба полоски: a – после вырезки; б – после вырезки и удаления слоя толщиной h

Fig. 1. The measuring scheme of deflection of the strip: a – after cutting; b – after cutting and removing the layer with h thickness

а                                      б                                       в

Рис. 2. Схема измерения перемещений кольца: a – изменение диаметра после вырезки; б – изменение диаметра после вырезки и удаления слоя толщиной h ; в – изменение величины осевого смещения

Fig. 2. The measuring scheme of the ring displacements: a – diameter change after cutting; b – diameter change after cutting and removing the layer with h thickness; c – the axial displacement change

Комбинации расчетно-экспериментальных окружных ст₀ и осевых a_z остаточных напряжений в полосках о_п ( h ) и кольцах с_к ( h ) определяются в соответствии с методикой [43, 44, 9, 10, 15] по формулам

°_в ⁽ h ) — pa _z ⁽ h ) = ст k ⁽ h ) = 2

E 5 (0) Г H

DC I 2

-

-

лоски; H - толщина кольца; E , p - модуль Юнга и коэффициент Пуассона материала; L – длина полоски;

_D 4 sin v R ³ - R ³

Rr c    3v  R^2 - R2

– радиус центра тяжести поперечного сечения цилиндрической полоски;

1 E ( H - h ) ² d 5( h )

3     D_c ²       dh

+

4 E ( H - h ) 3 D

h

5( h ) —        5(5) d 5, (3)

³ DC 0

I ( h ) = ^±™L( R 2 - h ) ⁴

8 sin ^v [( R ₂ - h ) ³ - R ³ ] ²

V    ( R ₂ - h ) ² - R ²

^a _z ^{( h} ) -PO ^{( h} ) = ^a n ^{( h} ) =

____8 E_____f ( h ) « + 1 (0) fh L R ₂ (2 R ₂ sin | - R_c v ) L       dh d dh

,   (4)

где D_c = ( D + D ₂) / 2 - средний диаметр кольца; R ₂, R -наружный и внутренний радиусы цилиндрической по-

– момент инерции поперечного сечения полоски относительно нейтральной оси.

Решение системы (3) и (4) дает экспериментальные зависимости для осевых a_z ( h ) и окружных o₈ ( h ) остаточных напряжений:

^ X ⁽ h ) =   ^Т^ n ⁽ h ) ■ Ц^ к ⁽ h )],

1 -Ц

^ о ⁽ h ) = T^l^ к ⁽ h ) + ц° n ⁽ h ^)]' ¹ -Ц

Определение остаточных касательных напряжений в нагруженных слоях втулки осуществлялось по методике [45] на основе анализа кинетики осевого смещения берегов разреза кольца в процессе травления по формуле

Т X ( h ) = - 7 G 2 [ Hw (°) - ⁴( H - h ) w ( h ) +

6 n R

+ ( H - h )² dwh) + 2 j w £) d ^

где G - модуль упругости материала при сдвиге; w ( h ) -осевое смещение концов берегов кольца после разрезки и удаления слоя толщиной h ; R = ( R + R )/2 - средний радиус кольца.

На рис. 3 и 4 маркерами представлены «экспериментальные» (расчетно-экспериментальные) зависимости для компонент тензора остаточных напряжений в зависимости от глубины упрочненного слоя h = R ₂ - r ( R_x <  r <  R ₂) при двух величинах радиального усилия 200 и 300 Н соответственно, полученные на основе соотношений (3)–(6).

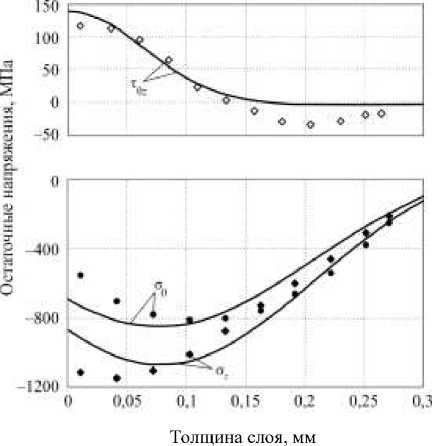
Рис. 3. Остаточные напряжения во втулках после алмазного выглаживания с радиальным усилием 200 Н: маркеры – расчетно-экспериментальные значения; сплошные линии – расчет по предложенной модели

Fig. 3. Residual stresses in the bushing after diamond smoothing with radial force 200 N: markers – experimental-computational values; solid lines – computation by the proposed model

Первичный анализ данных свидетельствует, что касательные напряжения Т8г по величине значительно меньше нормальных компонент az и ст0 (здесь и далее речь идет об абсолютных величинах напряжений). Так, на упрочненной поверхности (h = °) величина твг составляет около 20 % от сте и 9 % от cz, а по отношению к максимальным значениям az и сте максимальная величина твг не превосходит 12 %. Также можно отметить, что рассматриваемые величины радиального усилия алмазного наконечника слабо влияют на распределение и величину касательных напряжений.

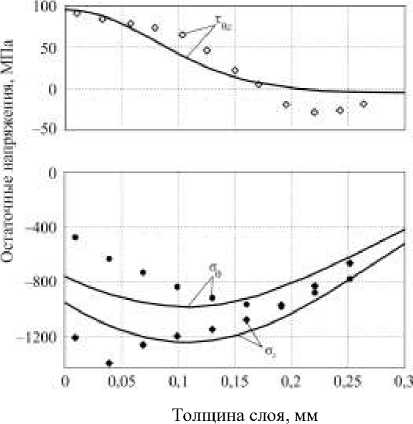
Рис. 4. Остаточные напряжения во втулках после алмазного выглаживания с радиальным усилием 300 Н: маркеры – расчетно-экспериментальные значения; сплошные линии – расчет по предложенной модели

Fig. 4. Residual stresses in the bushing after diamond smoothing with radial force 300 N: markers – experimental-computational values; solid lines – computation by the proposed model

Полученные экспериментальные данные позволяют рассмотреть вопрос (не)учета касательных напряжений в задачах усталостной прочности и релаксации остаточных напряжений в условиях ползучести. В ряде работ по оценке предела выносливости упрочненных цилиндрических изделий при изгибе в критериальных зависимостях для эквивалентного напряжения используется лишь интегральная величина компоненты az = az (h) в области сжатия. В этом типе задач учитывать компоненту Т8г не целесообразно, поскольку ее величина, во-первых, незначительна по сравнению с cz, во-вторых, интеграл, например, от интенсивности напряжений по области сжатия напряжения cz с учетом касательных напряжений даст крайне малую поправку (см. рис. 3 и 4). Однако в задачах релаксации остаточных напряжений вследствие ползучести ситуация иная. В частности, для случая на рис. 3 отношение интенсивности напряжений с учетом и без учета касательных напряжений составляет 1,046. Поэтому если ориентироваться на закон установившейся ползучести, в котором показатель нелинейности n в степенной аппроксимации скорости деформации ползучести от напряжения для современных материалов может принимать довольно большие значения (до n = 20), то, например, при h = 0 (на поверхности втулки) мы имеем увеличение скорости установившейся ползучести с учетом касательных напряжений для n = 8 в 1,43 раза, для n = 12 в 1,72 раза, а при n = 16 - в 2,05 раза. Поэтому ползучесть при учете касательных напряжений будет протекать существенно интенсивнее, что должно сказаться на увеличении скорости релаксации остаточных напряжений. Отсюда можно сделать предварительный вывод о целесообразности учета касательных напряжений в задачах ползучести упрочненных полых цилиндрических деталей при высоких показателях нелинейности в законе установившейся ползучести.

Настоящие экспериментальные исследования еще раз подтвердили анизотропный характер упрочнения при алмазном выглаживании [15–17] с различием эпюр для напряжений с₀ и с (при изотропном упрочнении зависимости для с_е = с_е ( h ) и с_ = с_ ( h ) практически совпадают), что отчетливо наблюдается на рис. 3 и 4.

3.    Математическая модель реконструкции напряженно-деформированного состояния после упрочнения

Необходимость математического описания кинетики напряженно-деформированного состояния упрочненных элементов конструкций в поле внешних температурно-силовых нагрузок приводит к постановке краевых задач с начальными данными для компонент тензоров остаточных напряжений и пластических деформаций, сформированными после процедуры упрочнения [42]. Это, в свою очередь, приводит к самостоятельной обратной задаче реконструкции распределения остаточных напряжений и пластических деформаций не только в приповерхностном слое, где частично известна экспериментальная информация о некоторых величинах компонент напряжений (см. рис. 3 и 4), но и по всей области интегрирования в краевой задаче с учетом выполнения уравнений равновесия и совместности деформаций. В настоящей работе для этой цели используется обобщение феноменологического метода моделирования напряженно-деформированного состояния в упрочненных цилиндрических деталях, развитого в работах [42, 15–17, 40] для случая отсутствия касательных напряжений. Выше было показано, что моделирование нормальных (диагональных) компонент тензоров напряжений и деформаций и недиагональных (касательных напряжений и сдвиговых деформаций) компонент можно осуществлять независимо. В связи с этим реконструкция остаточных напряжений с0, cz, сг и пластических деформаций q , q и q осуществляется по подробно изложенной в [15] методике, в соответствии с которой расчетные формулы принимают следующий вид:

r сr (r) = - Jg6(K)dK  R1 < r < R2,

'

q e ^{( r} ) =

(1 + v )(1 - 2 v) _x (1 + av )² E

2+a r 1+a-av xr 1+avjK 1+av (сr(K) + (1 + a)Ce(K))dK +

R

+ тг^+^т; (vc r(r)- (1 — v)ce(r)),

(1 + av) E qz(r) = aqe (rX  qr(r) = -qe (r)(1+a),(9)

s

2    R2  Г p2_p2 JK 4z (K "p(Cr ® + Ce ©)

R2  R1 R L       E_

сz(r) = E(e0 -q(r)) + v(cr(r) + ce(r)),(11)

где E - модуль Юнга; ц - коэффициент Пуассона; a -феноменологический параметр анизотропии упрочнения [15-17]. Величина a = 1 соответствует изотропной процедуре упрочнения в направлении осей z и e (гидро- и пневмодробеструйная обработка, термопластическое упрочнение, азотирование), а при a ^ 1 имеем неизотропное упрочнение (обкатка роликом, алмазное выглаживание, дорнование).

Из (7)–(11) следует, что если известны величина с_е = с₀ ( r ) и параметр a , то остальные величины определяются по следующей схеме:

^с е ^{( r} )    ⁽⁷⁾ >  ^с r ^{( r} )    ⁽⁸⁾ >  q e ^{( r} )    ⁽⁹⁾ >  q r ^{( r} ),     _{п 2)}

q_z ( r ) -^s Z -^с z ( r ).

Цифры над стрелками в (12) означают номер формулы, по которой рассчитывается величина.

Таким образом, феноменологическая модель (7)–(11) и схема (12) основаны на имеющихся экспериментальных данных о распределении компоненты с_е = с_е ( r ) . Однако экспериментально ее можно определить только в тонком упрочненном слое – области сжатия (см. рис. 3 и 4). Поэтому эти данные необходимо экстраполировать на всю область R <  r <  R . Для этого можно использовать аппроксимацию следующего вида [15]:

^с е ^{( r} ) = ( ^с о ^-с 1 ^exP [^{- (} R 2 ^{- r} * ^{- r )2} / b ² ] ) r^R ¹, (13)

где r * - значение радиуса, при котором экспериментальный график функции се = се (r) достигает локаль- ного минимума; о0, о, и b - параметры, подлежащие определению.

Однако на практике величина параметра анизотропии упрочнения а в (9) неизвестна, и ее можно определить только после проведения экспериментальных исследований. В этом случае схема (12) изменяется, и в качестве исходной информации необходимо иметь экспериментальные зависимости для компонент о₈ ( г ) и o_z ( г ) в упрочненном слое, а параметр а подлежит процедуре идентификации. Здесь на первом этапе определяются параметры о₀, о и b из решения системы алгебраических уравнений, которая формируется с учетом условий

°₉ ⁽ г *) = ° *, °₈ ⁽ r ₀) = 0,               (14)

где о * - экспериментальное значение минимума функции о₈ = о₈ ( г ) ; г₀ - значение радиуса, при котором функция о₀ обращается в нуль, и условия самоуравно-вешенности эпюры окружной компоненты напряжения

R2

|ов (г)dr = j d (гог (г)) = 0 ,

Ri следующего из первого уравнения (1) и граничных условий ог (R) = ог (R ) = 0 . Далее задача сводится к поисковому методу оптимизации: целенаправленно варьируются параметры г , г * , о * , которые, в свою очередь, варьируют параметры аппроксимации (13) и а , и для каждой такой совокупности значений этих параметров осуществляется численный расчет по схеме (12) до достижения минимума функционала:

А_в + A_z ^ min;

^ N 1( о, ( Гк ) -о, ( г ) ) ² 1 ²

^А - = ^L N ' ,  _v^k      ,       z ,     (16)

L    Lk=i(o-(r))      J где A; - функционал нормированного среднеквадратического отклонения расчетных значений о, (r) от соответствующих экспериментальных значений о, (г); N -число точек дискретизации радиуса r в упрочненном слое, в которых известны экспериментальные и расчетные значения окружной и осевой компонент тензора остаточных напряжений.

Поскольку влияние диагональных компонент тензоров остаточных напряжений и пластических деформаций на формирование остаточных касательных напряжений и сдвиговых деформаций отсутствует, для величины T_8z = т_8z ( г ) достаточно выполнить аппроксимацию экспериментальных данных при выполнении второго условия (2). Исходя из характера экспериментальной зависимости для касательного напряжения (см. рис. 3 и 4) для этой цели можно использовать следующее соотношение:

^т а z ^{( г} ) = ^т 0 ^-т 1 b ^ exp ( ^-( R 2 ^{- г )2} / b i² ) , R 1 ^ ^г ^ R 2 ,    ⁽¹⁷⁾

r где параметры т0, т, и b в первом приближении определяются с использованием характерных значений функции: таz =таz(г): т0z(R) = т* и т0z(г) = 0 (т* -

«экспериментальное» значение компоненты т_в2 на поверхности втулки, r – значение радиуса, где компонента т_в2 обращается в нуль) и аналога уравнения само-уравновешенности – второго условия (2). Затем вблизи окрестности полученных значений варьируются параметры b , т * , г , и минимизируется функционал A_6z нормированного среднеквадратического отклонения расчетных значений т_8z ( г_к ) от соответствующих экспериментальных значений т_8z ( г_к ), аналогичный по выражению (16), так, чтобы выполнялось условие (2).

Для определения распределения сдвиговой компоненты тензора остаточных пластических деформаций воспользуемся соотношением у8z (г) = гу . Представляя деформацию сдвига аддитивной составляющей упругой компоненты уz6 = тг8 (г) / G и пластической компоненты у 0z, имеем тг7(г) + УРв (г) = гV .                (18)

G

Здесь y_0z - полная деформация сдвига; v - относительный угол закручивания; G = E / ( 2(1 + ц ) ) - модуль сдвига материала.

В соотношении (18) неизвестны у Р ₆ ( г ) и v ■ Для конкретизации (17) проанализируем графики касательных напряжений на рис. 3 и 4. Толщина стенки упрочненной втулки H = R - R = 3,25 мм, а глубина залегания наиболее интенсивных касательных напряжений составляет 150 и 170 мкм соответственно, т.е. величина H больше глубины залегания в 22 и 19 раз, почти на два порядка. Поэтому в первом приближении можно ввести гипотезу, что интегральная величина угла закручивания V втулки после упрочнения близка к нулю ( у» 0). Тогда из (18) находим

Y P ( г ) = -т г ₆ ( г )/ G ,                (19)

где т_ге( г ) определяется формулой (17).

4.    Результаты расчетов и анализ результатов

Для идентификации параметров разработанной математической модели использовались данные для «экспериментальных» компонент тензора остаточных напряжений о0, ог и т8z, представленных на рис. 3 и 4, при усилии прижима (радиальном усилии) алмазного наконечника, равном 200 Н (вариант 1) и 300 Н (вариант 2). Значения параметров для аналитических зависи- мостей (13) и (17), полученные по методике, изложенной в подразд. 3, а также величина параметра анизотропии упрочнения α представлены в табл. 1.

Результаты расчетов компонент напряжений σ , σ , σ и τ по разработанной методике с параметрами из табл. 1 приведены на рис. 3 и 4 сплошными линиями и в табл. 2. Здесь же приведены значения среднеквадратических отклонений расчетных данных от экспериментальных (величины с чертой) для компонент напряжений σ , σ и τ для обоих вариантов технологической обработки втулок. В целом наблюдается удовлетворительное соответствие расчетных и экспериментальных данных. Отметим, что расчетные значения компоненты σ на два-три порядка меньше значений σ и σ (по абсолютной величине). Величина параметра анизотропии упрочнения α для обоих вариантов обработки принимает значение, равное 1,6. Собственно, введением величины α≠1 и удалось описать различие эпюр σ = σ (r) и σ = σ (r) в рассматриваемой здесь задаче.

Таблица 1

Значения параметров аппроксимации окружной и касательной компонент тензора остаточных напряжений

The values of the approximation parameters for the circumferential and tangential components of the residual stress tensor

Table 1

	Режим упрочнения [Hardening mode]
	σ , MПa	σ , MПa	b , мм	α	τ , MПa	τ , MПa	b , мм
Вариант 1 [First mode]	8,15	57,58	0,18466	1,6	–4,00	–41328,63	0,08972
Вариант 2 [Second mode]	17,00	91,88	0,23957	1,6	–3,50	–22092,16	0,11481

Таблица 2

Экспериментальные и расчетные значения компонент тензора остаточных напряжений и их среднеквадратическое отклонение друг от друга

Experimental and calculated values of the residual stress tensor components and their standard deviation from each other

Table 2

Глубина [Depth] h , мм	σ θ	σθ	σ z	σ z	σ r	Глубина [Depth] h , мм	τθ z	τθ z
Режим упрочнения по варианту 1, МПа [Hardening by the first mode, MPa]
0,01 0,04 0,07 0,10 0,13 0,16 0,19 0,22 0,25 0,27	–555,32 –704,63 –779,30 –809,84 –799,55 –755,24 –660,06 –537,49 –377,80 –250,79	–728,89 –811,25 –847,51 –830,92 –765,31 –661,02 –528,33 –401,35 –267,41 –193,63	–1119,21 –1149,67 –1102,04 –1006,93 –877,73 –731,47 –605,58 –466,19 –309,74 –216,76	–914,57 –1019,44 –1066,60 –1044,37 –960,50 –833,24 –671,98 –500,76 –342,78 –244,61	0,30 1,21 2,21 3,24 4,18 4,99 5,70 6,25 6,64 6,82	0,01 0,04 0,06 0,09 0,11 0,13 0,16 0,18 0,21 0,23 0,25 0,27	117,54 113,26 96,05 64,54 23,50 2,74 –13,19 –30,32 –34,37 –29,04 –19,62 –17,67	138,24 118,72 87,66 55,11 28,94 11,92 2,78 –1,49 –3,20 –3,80 –3,94 –3,98
	Δ=0,0272		Δ=0,0145		–		Δ=0,0869
Режим упрочнения по варианту 2, МПа [Hardening by the second mode, MPa							]
0,01 0,04 0,07 0,10 0,13 0,16 0,19 0,22 0,25	–480,78 –632,94 –730,94 –842,02 –920,61 –966,70 –984,72 –885,76 –784,64	–796,33 –889,03 –952,09 –980,02 –970,44 –924,43 –843,29 –735,76 –615,60	–1203,89 –1386,40 –1254,92 –1192,72 –1145,80 –1074,98 –965,20 –827,27 –663,40	–996,38 –1114,39 –1195,05 –1231,40 –1219,19 –1160,66 –1061,84 –931,68 –775,91	0,30 1,29 2,37 3,51 4,69 5,81 6,86 7,80 8,63	0,01 0,03 0,06 0,08 0,10 0,13 0,15 0,17 0,20 0,22 0,24 0,26	90,92 83,42 78,48 73,83 64,88 46,52 22,40 5,50 –18,56 –27,58 –25,48 –17,70	94,33 87,42 73,19 57,78 40,58 26,68 14,46 7,33 2,01 –0,96 –2,36 –2,98
	Δ=0,0512		Δ=0,0154		–		Δ=0,0907

Отметим, что глубина залегания отрицательных значений окружных и нормальных компонент остаточных напряжений в два раза больше, чем глубина области положительных касательных напряжений большой интенсивности.

Заключение

Выполненные исследования свидетельствует о том, что разработанная методика позволяет полностью выполнить реконструкцию и остаточных напряжений, и остаточных пластических деформаций, при этом авторами в модели впервые учтены недиагональные компоненты тензоров напряжений и деформаций.

Отметим, что реконструкция напряженно-деформированного состояния не является самоцелью (хотя важность решения этой задачи очевидна), и она – составная часть более сложных задач, таких как устойчивость наведенных остаточных напряжений к температурносиловым нагрузкам в условиях ползучести. Решение этой проблемы приводит к новым краевым задачам реологи- ческого деформирования с начальным напряженно-деформированным состоянием, методика реконструкции которого и представлена в данной работе применительно к поверхностно упрочненным втулкам из стали ЭИ691 (13Х11Н2В2МФ) после алмазного выглаживания.