Математическое моделирование некоторых особенностей диссоциации газовых гидратов

Диссоциация газовых гидратов (далее просто гидратов) является сложным процессом, кинетика которого зависит от термобарического и фазового состояния среды, окружающей гидрат и «истории» их образования, т. е. температуры и давления, компонентного состава газа-гидратообра-зователя. Процесс диссоциации, осуществляемый в промышленных условиях, с комбинацией этих факторов зачастую приводит к непредсказуемым

результатам. В частности, при изотермическом сбросе давления до величины ниже равновесной проявляется состояние метастабильности гидратов, выражающееся эффектами самокон-сервации и консервации. Процесс диссоциации гидратов, находящихся в этом состоянии, характеризуется его замедлением настолько, что гидраты продолжают существовать длительное время, хотя по данным из фазовых диаграмм они должны разлагаться.

Предупреждение или использование в технологиях газовой и нефтяной промышленности метастабильности в процессе диссоциации гидратов требуют умения рассчитывать ее параметры. Для решения этой проблемы необходимо развивать физико-математический аппарат.

Известные методы расчета и исследования диссоциации в основном описывают этот процесс с подводом к гидрату тепла. Однако при использовании для диссоциации метода снижения давления проявляются состояния метастабильности гидратов – эффекты самоконсервации и консервации, открытые российскими и зарубежными исследователями В.С. Якушевым, В.А. Истоминым [1], Д.В. Дэвидсоном (D.W. Davidson) [2] и Ю.П. Хэндой (Y.P. Handa) [3]. Имеющиеся в литературе описания эффектов метастабильности получены в результате экспериментов с гидратами из однокомпонентных газов и для конкретных термобарических условий. Имеющиеся зависимости для одних гидратных систем не распространяются на другие, в связи с чем их применение при решении практических задач, например, с добычей газа из природных гидратов или ликвидацией техногенных в широком диапазоне термобарических условий затруднительно. Поэтому создание метода расчета основных параметров процесса диссоциации гидратов, состоящих из многокомпонентных газов, в широком диапазоне изменения давления является актуальной задачей.

С целью ее решения разработана физикоматематическая модель, описывающая особенности диссоциации гидратов в изотермических условиях снижения давления окружающей гидрат среды ниже величины равновесного давления его существования.

Результаты и обсуждение

При разработке модели в качестве граничных условий принято то, что:

• ─    гидрат образован из одно- или многокомпонентного газа;

• ─    гидрат состоит из наиболее распространенных в природе кристаллических структур КС-I и КС-II;

─ исходное давление внутри гидрата постоянно и равняется величине, соответствующей условиям его образования;

• ─    температура окружающей гидрат среды постоянна и равняется температуре его образования;

─ гидрат, находясь в окружающей среде, может свободно диссоциировать, не повышая ее давления.

В зависимости от разности давлений внутри гидрата P 1 и окружающей его среды P 2 процесс диссоциации может протекать следующим образом.

Когда величина этой разности меньше или равна прочности σ гидрата на растяжение

1 >

- P

σ

сохраняется его механическая целостность.

Если величина этой разности больше величины σ

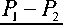
σ

гидрат, согласно закону Гука, механически разрушается.

Прочность на растяжение зависит от внутренней морфологии гидрата, на которую влияют состав газа-гидратообразователя, степени заполнения им полостей кристаллической решетки, содержания в ней воды, давле- ния и температуры роста кристаллов и т. д.:

о = f, ( y ;9; n ; P ; T )             (3)

В то же время, в характеристику внутренней морфологии гидрата в качестве основного параметра входит его плотность, которая также зависит от вышеперечисленных факторов:

p h = f ^ ( y ;9; n ; P ; T ) (4)

Кроме этого, внутренняя морфология гидрата характеризуется межкристаллитными взаимодействиями, объединяющими и связующими между собой кристаллы гидрата. В первом приближении эти взаимодействия можно выразить через основные параметры σ и ρ h , отражающие внутреннюю морфологию гидрата:

ф = ° (5)

ρh

Величина φ имеет размерность кДж/кг. Выражение (5) в принципе отражает удельную энергию межкристаллитных связей внутренней морфологии гидрата. Для ее нахождения необходимо знать величины σ и ρ h . Плотность гидрата ρ h рассчитывается по методике [4].

Аналитическое определение величины σ затруднено отсутствием вида функции f 1 . В связи с этим авторы определяли прочность гидратов, основываясь на известном факте [5], что прочность гидрата примерно в полтора-два раза превышает прочность льда. Используя экспериментальные данные [6] о прочности льда на растяжение, рассчитывались величины прочности гидратов на растяжение. В результате чего получена область примерных значений прочности гидратовв диапазоне температур от 230 до 280 К, изображенная на рисунке 1.

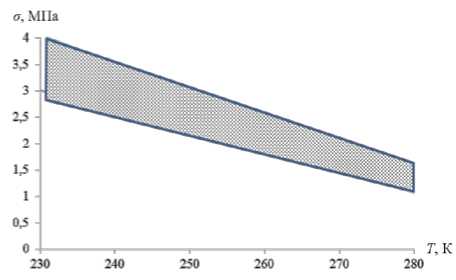
Рисунок 1. Область значений прочности гидратов на растяжение σ в зависимости от температуры T

Figure1. The range of strengths of hydrates for tension σ as a function of temperature T

В зависимости от прочности на растяжение процесс диссоциации может протекать по двум основным направлениям, схематично представленным на рисунках 2 и 3, с сохранением механической целостности гидрата или при его разрушении.

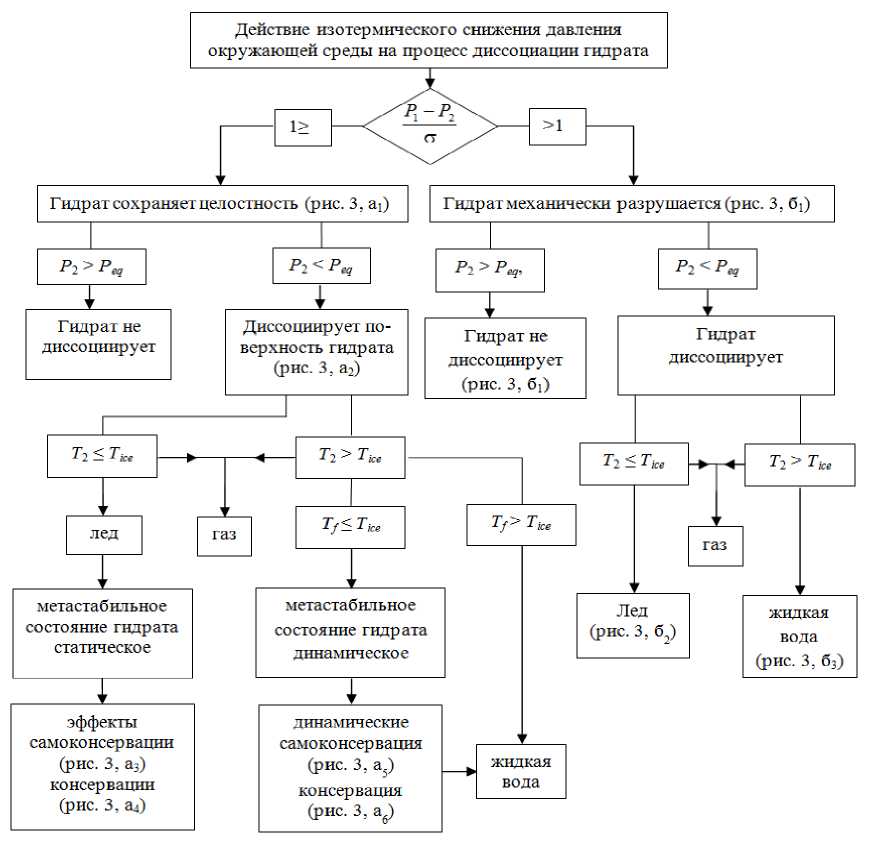
Рисунок 2. Схема направлений течения процесса разрушения и диссоциации гидрата при изотермическом снижении давления окружающей его среды: P 1 – давление внутри гидрата; P 2 – давление среды, окружающей среды; σ – механическая прочность гидрата на растяжение; P еq – давление существования гидрата на линии его равновесия; T 2 – температура среды, окружающей гидрат; T iсе – температура воды на линии ее равновесия жидкой и твердой фаз; T f – температура на поверхности гидрата

Figure 2. Scheme of the directions of flow of the process of destruction and dissociation of the hydrate under isothermal reduction of the pressure of its environment: P 1 is the pressure inside the hydrate; P 2 is the pressure of the medium, the environment; σ is the mechanical strength of the hydrate for tension; P eq – the pressure of the existence of hydrate on the line of its equilibrium; T 2 is the temperature of the medium surrounding the hydrate; T ice – water temperature on the line of its equilibrium of liquid and solid phases; T f is the temperature at the surface of the hydrate

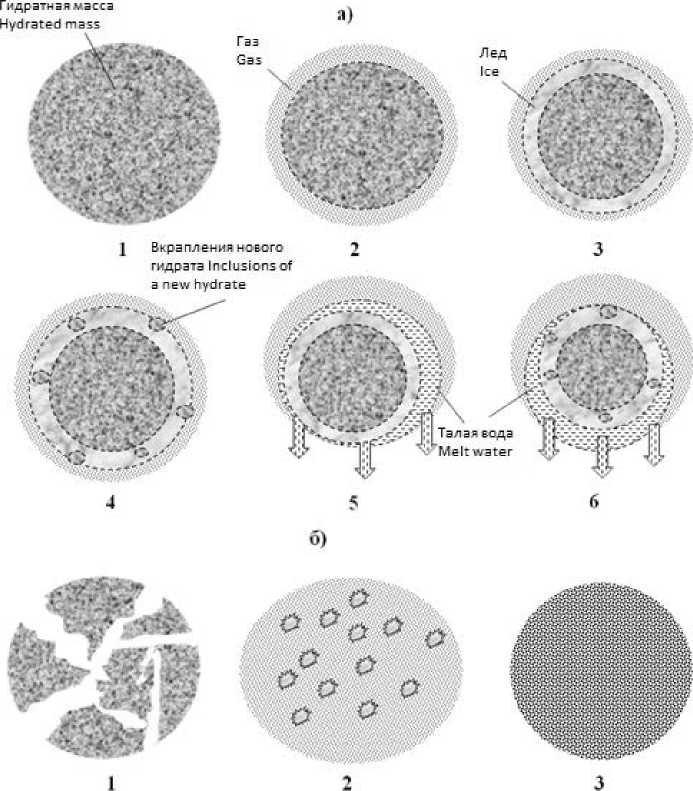
Рисунок 3. Разрушение и диссоциация гидрата от разности давлений Δ P окружающей среды и внутри гидрата: а ) – (Δ P /σ) ≤ 1 : a 1 – гидрат сохраняет целостность; a 2 –диссоциирует поверхность гидрата; a 3,4 – статическое метастабильное состояние гидрата (эффекты самоконсервации и консервации); a 5,6 – динамическое метастабильное состояние (динамические самоконсервация и консервация); б ) – (Δ P /σ) > 1: б 1 – механическое разрушение гидрата; б 2,3 – диссоциация разрушенного гидрата на газ и диспергированные лед и жидкую воду

Figure 3. The destruction and dissociation of the hydrate from the pressure difference ΔP of the environment and inside the hydrate: a) – (ΔP / σ) ≤ 1 : a 1 – hydrate preserves integrity; a 2 – dissociates the surface of the hydrate; a 3,4 – static metastable state of hydrate (effects of self-conservation and conservation); a 5,6 – dynamic metastable state (dynamic self-preservation and conservation); b) – (ΔP / σ) >1: b 1 – mechanical destruction of hydrate; b 2,3 – dissociation of the destroyed hydrate into gas and dispersed ice and liquid water

Диссоциация механически целого гидрата

Если выполняется условие (1) и в случае, когда давление окружающей среды P 2 больше давления существования гидрата на линии его равновесия P еq

P 2 >  P eq (6)

диссоциации в плане распада гидратной системы на молекулярном уровне не происходит (не разрушается кристаллическая решетка). Таким образом, при условиях (1) и (6) гидрат не разрушается и не диссоциирует (рис. 3, а 1 ).

С продолжением снижения давления окружающей среды до величины, меньшей давления гидрата на линии его равновесия P еq

P 2 <  P eq (7)

и при выполнении условия (1) сохраняется механическая целостность гидрата, но его поверхность диссоциирует с разложением кристаллической структуры на газ и воду (рисунок 3, а 2 ). При этом вода находится в твердом или жидком состоянии.

Вода находится в стабильном твердом состоянии при давлении P 2 и температуре окружающей гидрат среды T 2 меньшей или равной величины T iсе температуры воды на линии ее равновесия твердой и жидкой фаз:

T 2 ^ T ice (8)

Температура T iсе воды на линии ее равновесия жидкой и твердой фаз зависит от давления окружающей ее среды P 2 и рассчитывается в диапазоне от 0.1 до 210 МПа по формуле, полученной авторами на основе обобщения экспериментальных данных [7]:

T ce = 273.16 - 0.0731 • P 2 - 0.0002 • P ₂ ² (9)

При выполнении условия (8) на поверхности гидрата накапливается лед (рисунок 3, а 3 ) и газовая фаза, высвобождающаяся в процессе диссоциации, вынуждена диффундировать сквозь него. В связи с тем, что величины коэффициентов диффузии газа сквозь лед невелики, например, в диапазоне температур 168.00–272.65 К для метана они составляют 10^–14–10^–11 м /с [8], этот процесс медленный. Общее количество молекул газа N G , диффундирующего через поверхностный слой за счет разности давлений внутри шарообразного гидрата массой в 1 кг и плотностью ρ h , кг/м³, и окружающей его среды рассчитывается из уравнения:

n_g = A c =•   f ^T • ( P — P )      (10)

G ice                       1      2

k B • T • 5

где k В – константа Больцмана (1.38×10^-23 Дж/К); D iсе – коэффициент диффузии газа через лед, м²/с; f и δ – площадь и толщина поверхностного слоя, м² и м; τ – время процесса диффузии, с.

Толщина δ льда в процессе диссоциации поверхности гидрата увеличивается за счет его накопления, что ведет к замедлению выделения

X =

k _I

E m.

G des I

k II

Z m.

G des II i

+ ^=-----

где m , m – количество молекул i-го GdesIi GdesII i компонента выделяющегося газа из полостей гидратных структур КС-I и КС-II (может быть рассчитано по методике [10]); kI и kII – число компонентов газа, выделяющего из гидратных структур КС-I и КС-II; 8 и 24 – количество малых и больших полостей в кристаллических решетках гидратных структур КС-I и КС-II.

Для оценки кинетики процесса диссоциации гидрата, находящегося в состоянии самоконсервации, на рисунке 4 представлена графическая зависимость скорости диссоциации от разности давлений Δ P внутри гидрата и окружающей его среды.

газа и, следовательно, к уменьшению интен-

сивности процесса.

В этом случае состояние гидрата метастабильно, а его проявление в таком виде называют эффектом самоконсервации [9].

Скорость выделения диффундирующего

газа сквозь лед рассчитывается по уравне-

нию [кг/с]:

= D ice

•

W = Ng^M

^N А • ^T f • M _G

N А • k B • T 2 • 5

• ( P - P )

где N А – число Авогадро (6.02×10²³ моль^- ); M G – молекулярная масса газовой фазы, выделяющейся из гидрата, кг/моль.

Скорость диссоциации гидрата в таком метастабильном состоянии определяется по формуле:

W h 1

W

X

где X – массовая доля газа в гидрате:

Figure 4. Dependence of the dissociation rate W h 1 of methane hydrate under its static metastable state on the pressure difference ΔP

Зависимость получена для скорости W h 1 диссоциации 1 кг шарообразного гидрата метана плотностью 913 кг/м³, от воздействия разности давлений A P = P 1 - P 2 , МПа ( P 1 = 2.7 МПа), при температуре T 2 = 272.65 К поверхностного слоя толщиной δ = 1 мм и коэффициенте диффузии газа через лед D iсе = 10 ^–11 м²/с.

Как видно из графика, диссоциация гидрата протекает достаточно медленно. При этом необходимо отметить, что ее скорость в процессе будет снижаться в связи с уменьшением объема и площади его поверхности. Если поверхностный слой льда накапливается, скорость процесса диссоциации также уменьшается. Поэтому ее действительные значения будут меньше, представленных на графике (рисунок 4) , что согласуется с результатами экспериментальных исследований [11].

Если в газе, диффундирующем сквозь лед, имеются компоненты, из которых могут

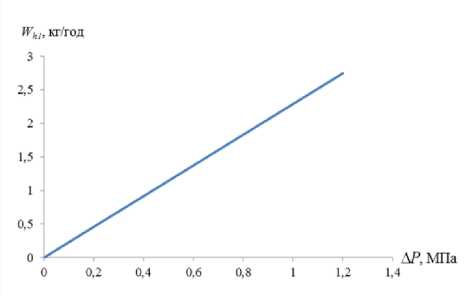
Рисунок 4. Зависимость скорости Wh1 диссоциации гидрата метана при его статическом метаста-бильном состоянии от разности давлений ΔP образовываться новые гидраты, стабильные при давлении окружающей среды P2 и условиях (1) и (8), то поверхностный слой будет состоять из смеси льда и нового гидрата – эффект консервации (рисунок 3, а4). Расчет образования новых гидратов выполняется по методике [10].

Общее количество молекул газа N G , диффундирующего через поверхностный слой, состоящий из смеси льда и нового гидрата, за счет разности давлений внутри гидрата и окружающей его среде рассчитывается из уравнения:

f -T / X

N G = fH ■ ( P - P 2 ) x k B ■ 5

X

Y ■ D ice- + ( 1 - Y ) ■ D h- T 2 T 2

где D h – коэффициент диффузии газа через новый гидрат, м²/с; Y – доля газа, проходящего сквозь лед; (1– Y ) – доля газа, проходящего сквозь гидрат.

Величины коэффициентов диффузии газа сквозь лед невелики, а через гидрат их значения еще меньше и составляют, например, для метана (1 ÷ 7)×10^-13 м²/с [12] в диапазоне температур 296.25–270.45 K, а для пропана (10^–14–10^–15) м²/с [13] в диапазоне температур 275.15–277.25 K. Учитывая то, что коэффициенты диффузии газа сквозь гидрат на два порядка меньше, чем через лед, в уравнении (14) вторым слагаемым в квадратных скобках можно пренебречь и при инженерных расчетах диссоциации гидрата, находящегося в метастабильном состоянии, допустимо пользоваться уравнениями (10) – (13).

Если соблюдаются услови е (7) и неравенство

T 2 >  T ce (15)

то к гидрату из окружающей среды притекает тепло. Если при (15) удельное количество тепла q, кДж/кг, больше или равно сумме удельных энергий диссоциации гидрата Edis и адиабатического расширения Eехр выделившегося при этом газа q>E, + E q dis exp то гидрат разлагается до жидкой воды и газа.

Величины E dis и E ехр рассчитываются из уравнений:

E,,. = BA  + Ea  - L dis des i       des n      h-iceI

⁺ L h - ice II ^{+ H} ice • ( n I ⁺ n il )

^E exp

R

^Y const x

Y -1" M G xT2 ■

P ¹

I P 2

7 - 1 ^γ

где E _des и E _des – энергии десорбции, затрачиваемые на выделение газа из гидратных полостей кристаллических структур КС-I и КС-II, кДж/кг; L _{h - ice}, и L _{h - ice}„ — энергии трансформации гидратных структур КС-I и КС-II влед, кДж/кг; H ice – энергия плавления льда (330–340 кДж/кг); n I и n II – гидратные числа для гидратов кристаллических структур КС-I и КС-II; γ – показатель адиабаты для выделившейся газовой фазы (для многоатомных газов γ ≈ 1.2867); R _const = 8.314 кДж/(кмоль×К) – универсальная газовая постоянная; M G – молекулярная масса газовой фазы, выделяющейся из гидрата, кг/кмоль. Энергетические параметры в выражении (17) рассчитываются по методике [10].

За счет расширения выделяющегося газа температура на поверхности гидрата T_f приобретает величину, рассчитываемую по формуле:

( Y - 1 )

()

Tf = T2 ■ Ph I к P2 )

В случае

Tf > Te(20)

вода остается в жидком состоянии.

Если температура на поверхности гидрата меньше или равна температуры образования льда

Tf ^ Tee(21)

то на поверхности гидрата за счет выделяющегося в процессе диссоциации холода образуется слой льда (рисунок 3, а 5 ), возможно, с содержанием нового гидрата (рисунок 3, а 6 ). Такой слой находится в динамически равновесном состоянии, т. е. он образуется с внутренней стороны диссоциирующего гидрата и тает под воздействием тепла окружающей среды. Проявляется эффект динамической консервации (рисунок 3, а 6 ). В случае образования на поверхности гидрата слоя из тающего льда и воды – эффект динамической самоконсервации (рисунок 3, а 5 ). Оба этих эффекта служат примером динамического метастабильного состояния гидрата.

Поскольку поверхностный слой образуется и тает, скорость диссоциации гидрата зависит от диффузионных процессов сквозь поверхностный слой и от теплового воздействия на него. В связи с тем, что для поверхностного слоя, находящегося в динамическом состоянии, характерны переходные явления, проявляющиеся в исчезновении его сплошности и ее восстановлении, математически учесть диффузионные процессы в кинетике диссоциации очень сложно. Поэтому при описании кинетики процесса диссоциации принято то, что во время этого процесса на гидрат влияют энергии тепла и депрессии. Скорость диссоциации гидрата при его динамическом метастабильном состоянии рассчитывается по формуле:

Q + (P -P2>•V w„ =-----— h2

dis + exp

где V – удельный объем 1 кг гидрата, м³, плотностью ρ h , кг/м³; τ Р – интервал времени, в течение которого происходило снижение давления от значения Р 1 до величины Р 2 , с; Q – тепло, притекающее из окружающей среды к гидрату, кДж/с:

Q = K • f • ( T ₂ - T f >  (23)

где K – коэффициент теплопередачи, Дж/(с×м²×К), зависящий от состояния и динамики среды, поверхностных (шероховатость, форма) и структурных (пористость, проницаемость) параметров гидрата.

Для оценки кинетики процесса диссоциации гидрата в этих условиях на рисунке 5 представлена графическая зависимость скорости W h диссоциации 1 кг шарообразного гидрата метана плотностью 913 кг/м³, от разности давлений P 1 и P 2 при P 1 = 6.2 МПа, температуре окружающей среды 280 К и коэффициенте теплопередачи 10 Дж/(с×м² × К) и времени τ = 10 с.

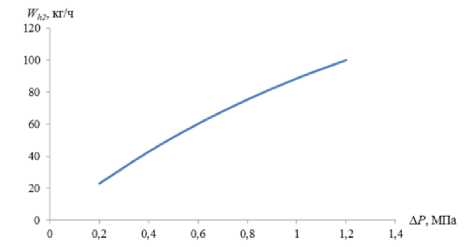
Рисунок 5. Скорость W h 2 диссоциации гидрата метана при его динамическом метастабильном состоянии в зависимости от разности давлений ΔP

Figure 5. The W h 2 dissociation rate of methane hydrate at its dynamic metastable state as a function of the pressure difference ΔP

Как видно из графиков на рисунке 4 и 5, скорость диссоциации гидратов, находящихся в статическом и динамическом метастабиль-ных состояниях различаются. Причем, величина скорости диссоциации гидрата в динамическом метастабильном состоянии превышает скорость его диссоциации в статическом метаста-бильном состоянии более чем в 106 раз.

Основной особенностью диссоциации гидрата в условиях сохранения его механической целостности является то, что процесс происходит на его поверхности с разложением кристаллической структуры на газ и воду.

Если температура окружающей среды меньше температуры воды на линии ее равновесия жидкой и твердой фаз, то диссоциирующая поверхность переходит в статическое метаста-бильное состояние, проявляющееся в виде образования на ней льда и, возможно, нового гидрата – эффектов самоконсервации и консервации. Диссоциация гидрата в этом случае в основном происходит за счет диффузии газа сквозь лед. Поэтому статическое метастабиль-ное состояние замедляет скорость диссоциации гидрата и способствует продлению времени его существования.

В случае, когда температура окружающей среды превышает температуру воды на линии ее равновесия жидкой и твердой фаз, диссоциирующая поверхность гидрата переходит в динамическое метастабильное состояние, характеризующееся таянием льда за счет тепла окружающей среды. В этом случае скорость диссоциации зависит от тепловой энергии и энергии депрессии. Поэтому ее величина существенно превышает скорость диссоциации гидрата в условиях статической метастабильности.

Депрессионный процесс механического разрушения и диссоциации гидрата

Процесс механического разрушения гидрата по всему объему за счет депрессионного воздействия (2) может не сопровождаться диссоциацией на молекулярном уровне (рисунок 3, б 1 ), если величина давления окружающей среды больше величины равновесного давления гидрата (6). В этом случае, скорость его разрушения, кг/с, выражается в виде:

W h 3

= V • ( P i — P 2 >

T p • Ф

Механическое разрушение гидрата под действием депрессии может идти до частиц микрометрических размеров. Необходимо отметить, что частицы могут: находиться в свободном диспергированном состоянии, коалесцировать, образовывать конгломераты. В связи с чем, суммарная площадь f ’ частиц, взаимодействующих с окружающей средой, в зависимости от их состояния может различаться на несколько порядков.

Дальнейшее уменьшение давления окружающей среды ниже величины равновесного давления гидрата

2 <  eq

приводит к диссоциации механически разрушенного гидрата.

Когда температура окружающей среды меньше или равна температуре воды на линии ее равновесия жидкой и твердой фаз

T < T 2 ice и при превышении или равенстве удельной энергии депрессии суммы удельных энергий межкристаллитных связей φ, разложения кристаллической решетки гидрата Eice и расширения Eexp выделяющегося из нее газа

• > ф + E_ + E exp         (26)

P h

E = E, + E, - L, . + L, .       (27)

ice desi des^ h - icei h - icen происходит диссоциация механически разрушенного гидрата до свободного газа и льда (рисунок 3, б2).

При температуре окружающей среды, превышающей температуру воды на линии ее равновесия жидкой и твердой фаз

T >  T

• 2 ice

и удельной энергии депрессии большей или равной сумме удельных энергий межкристаллитных связей φ, диссоциации гидрата E_dis и расширения E _exp выделяющегося газа

— >  ф + E dis + E exp        (28)

Ph то процесс диссоциации происходит до свободного газа и жидкой фазы воды (рисунок 3, б3).

Поскольку механическое разрушение гидрата может идти до частиц микрометрических размеров, выделяемые в процессе диссоциации лед и жидкая вода находятся в диспергированном состоянии (рисунок 3, б 2 и б 3 ).

Величины скоростей разрушения и диссоциации гидрата при условиях (26) и (28), соответственно, до льда и воды под воздействием депрессии рассчитываются по формулам:

• VPZP21 + Q

Wh^Ce = ф + E +E ice exp

Lf P z P ) + Q.

W„ =----^P-------- dis     ф + E.. + E dis exp

В (29) и (30) Q ’ – тепло, притекающее из окружающей среды к частицам механически разрушенного гидрата в процессе их диссоциации, кДж/с:

Q ' = f '• K •( T ₂ - T f )           (31)

где f ’ – суммарная площадь, м², частиц механически разрушенного гидрата, контактирующих с окружающей средой.

Для оценки кинетики процесса диссоциации механически разрушенного гидрата на рисунке 6 представлены графические зависимости скоростей W и W диссоциации гидрата hice               hdis метана с ρh = 913 кг/м3 и σ = 1.5 МПа, от разности давлений P1 и P2 при исходном давлении P1 = 3.5 МПа, температурах окружающей среды, соответственно, 270 и 275 К, коэффициенте теплопередачи 100 Дж/(с×м2×К) к суммарной площади частиц 1 м2 и времени τ = 10 с.

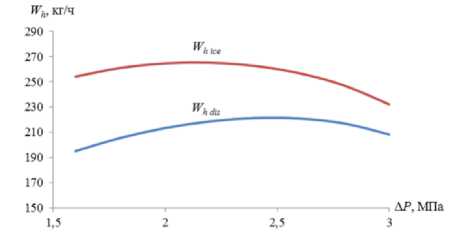
Рисунок 6. Скорость разрушения и диссоциации гидрата, соответственно, до льда W и воды W hice                        hdis под воздействием депрессииΔP

Figure 6. The rate of destruction and dissociation of the hydrate, respectively, to ice W and water under the hice influence Wh of depression ΔP

Как видно из графиковна рисунке 6, процесс разрушения и диссоциации гидрата до льда происходит интенсивнее, чем до жидкой воды в связи с тем, что при прочих равных условиях процесса удельные энергетические затраты на разложение кристаллической решетки гидрата до льда E_ic e (27) меньше чем на диссоциации гидрата до жидкой воды E_dis (17). Значения скоростей на обоих графиках вначале растут, имеют максимум, а затем уменьшаются. Уменьшение скорости диссоциации объясняется тем, что с увеличением депрессии Δ P уменьшается температура T_f (19) на поверхности диссоциирующих частиц и интенсивно увеличивается количество энергии E _exp (18), затрачиваемой на расширение выделяющегося газа.

Механическое разрушение гидрата под действием депрессии может идти до частиц микрометрических размеров, взаимодействующих с окружающей средой. Частицы могут находиться в диспергированном состоянии, коалесцировать и образовывать конгломераты. В зависимости от агрегатного состояния частиц, их взаимодействие с окружающей средой осуществляется интенсивно или замедленно. Во время этого взаимодействия, если давление окружающей среды превышает равновесное давление гидратов, то диссоциации не происходит.

В противном случае, если имеет место диссоциация гидрата с выделением газа и перестроением кристаллической решетки до льда или жидкой воды. Такая диссоциация происходит в условиях превышения удельной энергии депрессии над суммой удельных энергий межкристаллитных связей, разложения кристаллической решетки и расширения газа, выделяющегося в этом процессе. Интенсивность процесса диссоциации механически разрушенного гидрата превышает скорость диссоциации его целого образца. Выявлено, что диссоциация гидрата до льда происходит интенсивнее, чем до жидкой воды, при этом обоих случаях скорость диссоциации вначале растет, имеет максимум, а затем уменьшается. Этот экстремум обусловлен влиянием интенсивного роста энергии, затрачиваемой на расширение газа, выделяющегося в процессе диссоциации в зависимости от депрессионного воздействия на гидрат.

Заключение

Разработанная модель охватывает особенности процесса диссоциации целостных и механически разрушенных гидратов. С ее помощью рассчитываются условия и кинетические параметры процессов механического разрушения и диссоциации гидратов от изотермического депрессионного воздействия; проявления статических и динамических метастабильных состояний механически целых диссоциирующих гидратов.

С ее помощью выявлено:

─ статические метастабильные состояния механически целых гидратов возникаютв условиях снижения давления окружающей среды меньше равновесного существования гидратов и при температуре окружающей среды, не превышающей температуру чистой воды на линии ее равновесия твердой и жидкой фаз;