Математическое моделирование нестационарного теплообменного процесса и определение изменениятемпературы воздуха в подземном вентиляционном тракте

Введение. Задачей изучения процесса нестационарного теплообмена при движении воздуха в прямом цилиндрическом подземном канале занимались ряд ученые мира. Ими были получены определенные решении данной задачи. Анализ имеющихся решений изменения температуры приточного воздуха в подземных вентиляционных каналах показал, что для случая поступления в одиночный канал воздуха с переменной температурой уже имеются аналитические решения[1,6,7]. Они получены К.Ван-Хеерденом [2,4,7] и Е.В.Стефановым [3,5,8] при условии гармонических колебаний температуры входящего в канал воздуха. Е.В. Стефановым было доказано [3,5-8], что температура воздуха на выходе из канала без искажений воспроизводит изменения температуры воздуха на входе, но с некоторым запаздыванием во времени и изменением абсолютного значения. Поэтому оказалось целесообразным рассмотреть нестационарный теплообмен в одиночных подземных каналах при переменной температуре воздуха на входе с использованием теории систем автоматического регулирования, что позволило выявить параметры приточных подземных вентиляционных каналов как звена системы автоматического регулирования и получить решения в виде уравнения амплитудно - фазовой характеристики звена

— h - х ж     9

W(ia) = е

M/ ^ iN л

(ю)     (ю)

где M ( ^ ) = А ю ) -является вещественной частотной характеристикой; N ( ю ) = А. a ) -мнимая частотная характеристика.

Основная часть. Анализ решения (1), полученного на базе теории автоматического регулирования показывает, что его можно привести к виду, полученному Е.В.Стефановым. Для этого необходимо воспользоваться рекуррентными соотношениями для функций Томсона и в M ( ю ) и N ( ю ) перейти к определяющим процесс теплообмена критериям Био ( Bi ) и Предводителева ( Pd) , а передаточную функцию W ( ia ) рассматривать как отношение температуры воздуха на выходе из канала t ( х, т ) к температуре воздуха на входе в канал t ( о, т ). Тогда общее решение, характеризующее степень изменения температуры воздуха на выходе из подземного канала при

t ( о, т ) = A t Cos ют будет иметь вид:

—

t( х т) = е t(o т)

— (M + iN) v

Так как сдвиг колебаний ( iN ) температуры приточного воздуха, движущегося в подземном вентиляционном канале можно не учитывать [3], то степень изменения температуры воздуха на выходе из подземного канала выразится зависимостью

—

t(х Т ) = е t(o т)

h • х

М

или

tх т

t

О т

—

—

h • х и--M

-РА- = е 9 и гр

—

где   М, является функцией критериев в = 4 Pd и Bi, учитывает процесс распространения температур в окружающем канал массиве;

, а • S • 9

h =-------

Q уд

• x - расстояние от начального до рассматриваемого сечения канала, м;

• <9 - скорость движения воздуха в канале, м/с;

• а - коэффициент теплообмена движущегося воздуха и окружающего канал массива грунта, Вт/м ² , ⁰ С;

Для процесса охлаждения движущегося в подземном канале воздуха, т.е. использование аккумулированного холода весной и летом

а = 3,55 -90,8 • d

—

0,2 —т—;  или а = 3,05 • 90,8 • d

_{2 0} или         ,

м • С

—

0,2 ккал

20, м • ч • С

Для процесса нагревания движущегося в подземном канале воздуха, т.е. аккумуляция холода зимой или

/ л - 0,054

x

^ d)

Вт

м • С

/ \ - 0,054

X

I d )

Примечание: при скорости движения воздуха

ккал

2    0;

м • ч • С

& >  10 м/с разность эффективностей

• и гр - температура окружающего канал грунта, ⁰ С;

Для построения номограммы по аналитическому выражению (3) приведем показатель экспоненциальной функции к окончательному виду

- — -М =- 0,00377 • M ^— --  (6)

Исходя из общей оценки всех возможных случаев работы приточных подземных одиночных воздуховодов, находящихся в неограниченном массиве, можно принять

а x d

следующие пределы величин в , Bi , — и &

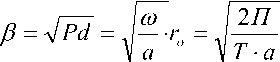
• Г о = 0,05 ^ 4,0

■ г

Bi =---°- = 0,5 ^ 40

Л

х

- = 25 ^ 4000 d

- = 0,01 - 5

• где Т – период колебаний, ч;

• а – коэффициент температуропроводности окружающего канал массива, м²/ч

• r 0 – радиус канала, м;

• d – диаметр канала, м;

• А - коэффициент теплопроводности окружающего канал грунта, Вт/м°С .

С целью выявления зависимости М = f (в) и М = f (Bi) были проделаны численные расчеты величины М при фиксированных Bi = (0,5 ^ 40) и в = (0,05 ^ 4,0). Результаты показали, что аппроксимация числа М возможна только для определенных областей значений Bi и в, что отражено в номограмме (Рис. 1), построенной для расчета изменения температуры приточного воздуха, движущегося в одиночных подземных вентиляционных каналах при неограниченном — и t0 = a A • cos ЮТ . Эффективность d Т t процесса изменения температуры движущегося в канале воздуха во всех случаях будет определяться величиной температурного напора между обменивающимися теплом средами, временем теплового взаимодействия приточного воздуха с грунтом и величиной поверхности теплообмена.

Отношение амплитуд колебаний температур воздуха представлено следующей зависимостью:

A

К I h

x = exp - кх

• A,    Л &

t ₀

О величина температурного напора можно судить по графикам, характеризующим температуру грунта и изменение во времени температуры наружного воздуха. Аналогичный график построен на рис.1 применительно к темпераурно-влажностным условиям Узбекистана[1,4,5,7].

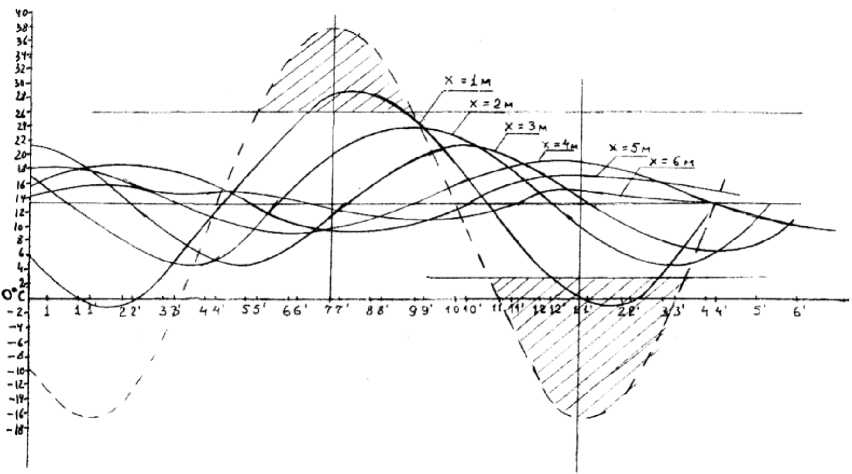
Рисунок 1 - График периодического изменения температуры наружного воздуха и соответствующий ей температуры грунта на глубинах от х= 1 м. до х= 6 м.

Условные обозначения:

__________график периодического изменения температуры наружного воздуха, ⁰ С.

______________ график периодического изменения температуры грунта на глубине

х= 1,2,3,4,5,6 м. 1, 2, 3,……. месяцы года.

Будем считать наилучшим случай, когда весной и летом поступает наружный воздух с температурой +26 ⁰ С, а зимой с температурой не ниже 0 ⁰ С. Из графика видно, что весной и летом средняя температура воздуха +26 ⁰ С и выше будет наблюдаться в течение 4^х месяцев, а зимой наружный воздух с t н =0⁰С и ниже будет поступать в СВ также в течение 4^х месяцев. Кроме того, на графике дана естественная температура окружающего канал грунта на различной глубине.

По графику мы можем судить:

• 1)    о величине температурного напора между обменивающимися теплом средам в начале процесса;

• 2)    о минимальном и максимальном снижении амплитуды колебаний температуры воздуха при движении в подземном вентиляционном канале;

• 3)    о характерном времени теплового взаимодействия грунта и воздуха. (Характерным будем считать тот отрезок времени, в течение которого происходит изменение температуры воздуха в результате теплообмена с окружающим канал грунтом).

И так мы можем сказать, что для каждого климатического района существует характерное время теплового взаимодействия приточного воздуха, движущегося в одиночном подземном вентиляционном канале, и грунта, а результаты этого теплообмена при to т = At ’ COS ®Т выраженные в изменении температуры приточного воздуха, определяется уравнением (3).

На основе выше приведенных математических уравнений была разработана компьютерная программа и в результате были получены спектр графиков зависимостей с ограниченной научной точностью [4,7,8].

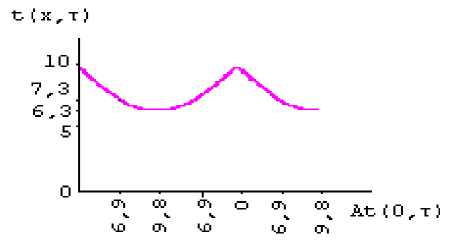
t(X,T)

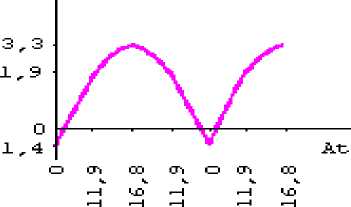
Б)

А)

Зависимость t ( x, т ) =fA _t(0, _T ) ). А ) -при нагреве; Б ) -при охлаждении.

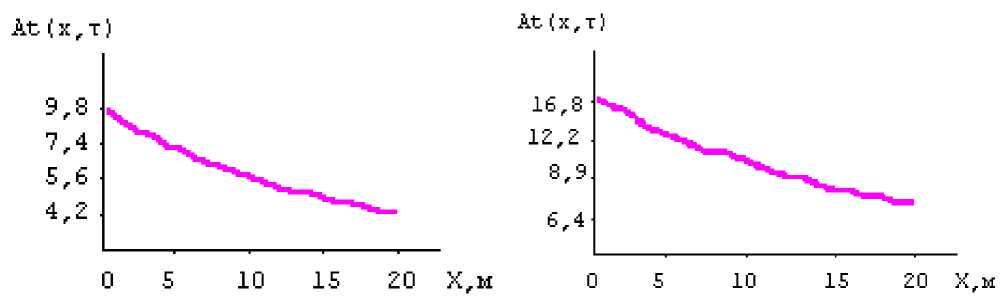
А )                                             Б)

Зависимость A t _{( х т} ) = f ( e ^{- nx} ) . А ) -при нагреве; В ) -при охлаждении.

Выводы. Исходя из вышеизложенного, можно сделать следующие выводы:

• 1.    Рассмотренный вариант решения изменения температуры приточного воздуха при движении в подземном канале при to т = At • COS СОТ как звена системы автоматического

• 2.    Построена номограмма для практических расчетов изменения температуры

  приточного воздуха, движущегося в

  
  

  величине относительного расстояния

  
  

• 3.    Учет данного изменения

  температуры приточного воздуха позволит более

  
  

• 4.    Графики зависимостей A_{t ( — т} ) = f ( e - nx ) , t ( x, T ) =f A _t(₀, _{T )} ) компьютерных моделей позволяет научно анализировать исследуемых физических процессов нагрева и охлаждения воздуха.

• 5.    Оптимизировать значения расчетных температур грунтового массива и тем самым добиться снижение установочной мощности оборудования систем холодоснабжения.

регулирования согласуется и приводится к решению, полученному в [3], а само решение приведено к виду (3,4), удобному для построения номограммы;

одиночном подземном канале при неограниченной

— и периоде колебаний температуры наружного d воздуха;

обоснованно подойти к выбору расчетных параметров наружного воздуха для СВ, снизить установочную мощность оборудования для холодоснабжения, уменьшить эксплуатационные расходы энергоресурсов, экономить моторесурсы холодильных машин.