Математическое моделирование неустойчивости тонкого слоя вязкой жидкости

В основе многих технологических процессов различных отраслей промышленности лежат процессы течения тонких слоев вязких жидкостей (жидких пленок). Жидкие пленки находят применение в энергетической, металлургической, пищевой, атомной, химической и других отраслях промышленности.

Широкое применение аппаратов, реализующих процессы течения тонких слоев вязких жидкостей, обусловлено их высокой эффективностью и экономичностью, незначительными затратами электроэнергии. Также жидкие пленки используются для термической защиты узлов и агрегатов различного оборудования [2, 3].

Течение жидких пленок неустойчиво даже при малых скоростях стекания, что приводит к возникновению и развитию на свободной поверхности тонкого слоя вязкой жидкости волновых возмущений, которые могут способствовать разрушению пленки, приводить к нарушению технологического процесса и аварийным ситуациям.

Избежать нарушений технологического процесса и аварийных ситуаций можно, управляя течением жидкого слоя или совершенствуя методы проектирования пленочных аппаратов и технологических систем. Для этого необходимо знать, какие физико-химические факторы и каким образом влияют на течение и его устойчивость. При этом экспериментальное исследование течений жидких пленок затруднено в силу сложности условий протекания пленочных процессов (большие температуры, высокие скорости течения, малая толщина жидкого слоя).

Математическое моделирование неустойчивости тонкого слоя вязкой жидкости и вычислительный эксперимент позволяют учесть различные физико-химические факторы, исследовать их влияние на неустойчивость жидкой пленки; дают возможность подробно изучить явления на поверхности раздела газ-жидкость; найти критические и оптимальные режимы работы пленочных аппаратов; получить некоторые аналитические зависимости. Это открывает путь к усовершенствованию методов расчета течений жидких пленок, способов конструирования пленочных аппаратов, позволяет предложить пути управления процессом.

В рамках математической модели неустойчивых режимов течения жидких пленок [1,2] иссле-

Г  Э  ,Адш     д⁴\у    д³ш  / \д²ш    Эш      Эш      Э²ш

\  дх ) dt     дх      8х            дх      ох       ох       дх д2\у ! Эу Эу dxdt дх dt

+«22

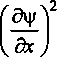
+ «26

Э\|/ Э²\|/ дх Эх²

д3ху

+ «28V—у+ «зо дх

Эху Э3\р

^dx дх3

д\ + V—г дх⁴

7 Эш 2 Э²Ш 2 Э²\у

+ «з?У ^ + «39^ —y+«4oY т^г+ дх дх         dxdt

Эш Эш Г Эш У Эш Э2ш Э3ш 2 Э4ш 2 53ш _...

+«444/——+«45V — +«49V^-—t + «51V-4 + «55V -7T+o58Y "УТ = ^О)

dx dt \дх ) дх дх2 дх3 дхдх

Rec

«1 =--

1       3

Re²FN ReM 3 _n3r.,          5 „          ReM _{n n}

«4 =--, «₆ =--H-- ReFIt + F), a₇ =—Re F, =--,a_n =-ReF-Ret,

4       2      6      2    40 v 7      24        12

au = -2ReF -Ret, «16 = -ReM + -Re3Fx +—R^F2, a,7

- 4a7, «22 — a16, «26 "" «4> «28 ~ ^«4» «зо — ЗЯр

• 14                   16            820

• 2.    Неустойчивость жидкой пленки в линейном приближении

a₃₁=-ReF,a₃g =-- — ^-R^Ft^R^F¹ , a₄₀ =6a₁₉ a_AA = 1207,045 =-/teM + -fl№

«49 = 2«4> «51 = 60], a55 = 3«j, «58 = 3a4

дована неустойчивость тонкого слоя вязкой жидкости (воды) в линейном и нелинейном приближениях. В линейном приближении на основе дисперсионного уравнения получены аналитические зависимости для волновых характеристик жидкой пленки, рассчитаны области неустойчивости, кривые максимального роста возмущений, фазовые и групповые скорости. В рамках нелинейного приближения предложен метод расчета областей неустойчивости жидкой пленки. Осуществлен сравнительный анализ полученных в линейном и нелинейном приближениях результатов.

ло Рейнольдса Re, число Фруда F, коэффициент поверхностной вязкости N, касательное напряжение на поверхности раздела газ-жидкость т, поверхностное натяжение ст, параметр Марангони М.

В рамках уравнения (1) проведено исследование неустойчивости жидкой пленки в линейном и нелинейном приближениях для чисел Рейнольдса Re <12.

Пусть на свободной поверхности жидкой пленки развивается монохроматическое возмущение \|/(х, 0 = A-exp(Kkx - (со, + /ю,)/)), где к - волно вое число, юг - частота, о, - инкремент.

Подставив монохроматическое возмущение у(х, 0 = A-exp(i(kx-(to_r+ ia>i)t)) в линейную часть уравнения (1), получим дисперсионное уравнение: (®_г + к»! )(«₇^ + г) + a_xk⁴ -a₄ik³ -а₆к² +a_xxik = 0. (2)

Дисперсионное уравнение (2) связывает волновые характеристики жидкой пленки с физико- химическими факторами ст, N, т, М и позволяет в явной форме выразить их, в частности, частоту <йг:

инкремент и, (рис. 2):

а_хк⁴ -а₆к² + а,к(а₄к³ -а_пк\ со, =-------------------------------

(лук) +1

найти фазовую скорость С (рис. 3):

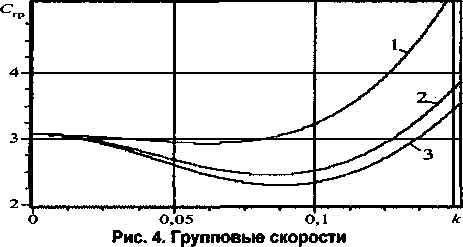
С = <йг(к, групповую скорость Срр (рис. 4): Cjp = dmjdk.

Расчет волновых характеристик позволяет оценить эффективность протекающих на поверхности раздела газ-жидкость процессов [4].

Инкремент неустойчивого монохроматического возмущения с волновым числом к положителен, о, > 0, (рис. 2), что позволяет в линейном приближении рассчитать область неустойчивости жидкой пленки (рис. 5) в плоскости параметров (Re, к); также рассчитывается кривая максимального инкремента <о_|тах [5], соответствующая возмущениям, которые обладают наибольшей скоростью роста, с наибольшей вероятностью реализуются в эксперименте, оказывают наибольшее влияние на процесс течения жидкой пленки при работе пленочных аппаратов [6].

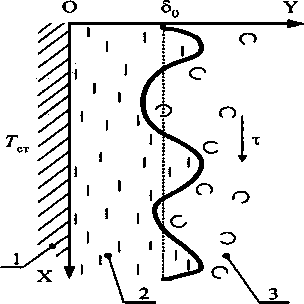
Рис. 1. Схема течения жидкой пленки:

1 - поверхность стекания;

2 - жидкая пленка;

3 - газовый поток

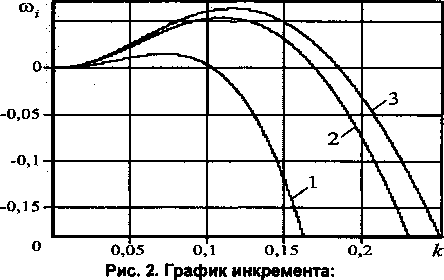
1 -Re = 5\

2-Re = 9\

3-Re=\0

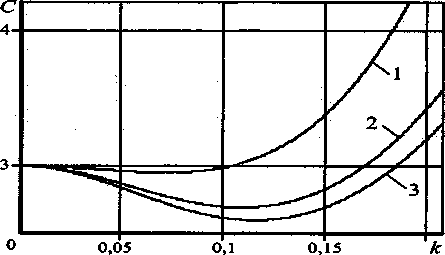
Рис. 3. График фазовых скоростей:

1 -Re = 5‘, 2-Re = 9; 3-Ле=10

A-Re = 5;

2-Re = 9;

3-Re = 10

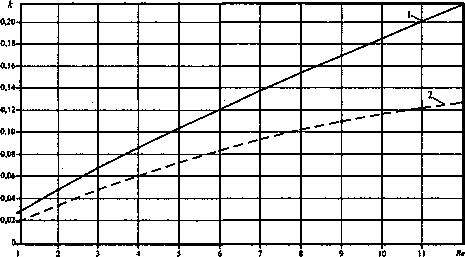
Рис. 5. Область неустойчивости в линейном приближении: 1 - кривая нейтральной устойчивости; 2 - кривая максимального инкремента

Расчет областей неустойчивости дает возможность выявить, какие физико-химические факторы оказывают стабилизирующее или дестабилизирующее влияние на течение жидкой пленки.

Известно, что присутствие НПАВ на поверхности раздела газ-жидкость стабилизирует течение, способствует уменьшению скоростей роста возмущений, фазовых, групповых скоростей; газовый поток оказывает стабилизирующее влияние на течение жидкой пленки в режиме прямотока и дестабилизирующее - в режиме противотока [4]. В условиях дестабилизации наблюдается увеличение скоростей роста возмущений, фазовых, групповых скоростей. При этом можно найти такие значения физикохимических факторов, при которых течение станет устойчивым [4] или, наоборот, жидкая пленка разрушится [2].

Вычислительный эксперимент для воды в условиях свободного стекания (т = 0, N = 0, М = 0) показал, что течение жидкой пленки неустойчиво во всем диапазоне чисел Рейнольдса Re < 12 (рис. 5).

Чем больше значение числа Рейнольдса Re, тем зона неустойчивости шире по диапазону волновых чисел к, выше максимальная скорость роста возмущений (рис. 2, табл. 1), тем меньше фазовые (рис. 3) и групповые (рис. 4) скорости.

Фазовые скорости неустойчивых возмущений меньше фазовых скоростей устойчивых возмущений (рис. 3). Расчеты показали, что минимальное значение фазовых скоростей С достигается на кривой максимального инкремента.

Таблица 1 Расчет кривых нейтральной устойчивости и максимального инкремента

Re	к
	®1 = 0	^imax
1	0,02714	0,01919	0,00022
5	0,10378	0,07245	0,01536
9	0,16937	0,10974	0,05464
10	0,18491	0,11628	0,06419

Групповые скорости Cq, неустойчивых возмущений меньше, чем групповые скорости устойчивых возмущений (рис. 4).

• 3.    Неустойчивость жидкой пленки в нелинейном приближении

Задача исследования неустойчивости течения тонкого слоя вязкой жидкости не исчерпывается линейным анализом. Учет нелинейностей позволяет уточнить результаты, полученные в линейной постановке, дает возможность выяснить влияние нелинейного взаимодействия возмущений на течение жидкой пленки.

Амплитуда возмущения, развивающегося на свободной поверхности жидкой пленки, представима в виде (7):

X(x,z,t) = Og e^^+ai е'(⁰¹(^^+Аи)+

+a2ev 1'+a3ex z'+a4ex Xl z(7) где ад - амплитуда несущей волны; ах, а2 - ампли- туда боковых волн; а3, а4 - наклонных волн.

^- = yog + Р₂ (2а₀а,а₂ sin А + 20003^4 sin А]) - dt

-0/Oq +2оь<^ *20^02 +2a₀a₃ +2a₀a₄ +

+2^0,а2 cos А + 2ооа3а4 cos А,);

at х                    7

-02(aQa2sin(-A)-2a2a3a4sin(A, -А))-

• - 0^200^ + а^ + 2а^ +2a,af +

+2а_ха₄ + ciga₂ cosA + 2a₂a₃a₄ cos(A, -A)j;

^" = -^A+^cit-^a2-at x                   1

-02^a1sin(-A)-2a1a3a4sin(A1 -A)j-

• — 0, (20^^ +2a_xa₂ +a₂ + 2a₂a₃ +

+2^04 +aQa_t cos(-A) + 2a,a₃a₄ cos(A, - A));

^ = (fczd2-^a3+V)a3-

• - 0₂ ^a₄ sin A, + 2a,a₂a₄ sin (A, - A) ) -

• - 0! (2^03+20^03 +2a₂a₃ + a₃ + 2a₃a₄ +

+a$a₄ cosA, + 2a,O2a₄ cos(A-A_t)j;

(Ю)

(П)

= "(Mi + ^-^аз - v)a₄ - at ^x                  '

-0₂(aQa₃sinA, +2a,a₂a₃sin(A₁ -A)j--0, (2^04 + 2a²a₄ + 2a² a₄ + 2aja₄ + a₄ + +OqO₃ cos A, + 2a,a₂a₃ cos (A, - A)); ^ = 40, (a,a₂ sin A + a₃a₄ sin A,) + +402 (a,a₂ cos A+a₃a₄ cos A,) + +0₂ (-2og + a² + a₂ ) - 2£²a₂ + +—(aQa₂sin(-A)-2a₂a₃a4sin(Ai -A)j-

• -—(aga₂ cos A+2a₂a₃a₄ cos(A, - A)} + +—^ao^a'i^siⁿ(^_^)^_2aia₃a₄sin(A] -A)j-

  
  

^1- = 40_т (а_ха₂ sin А + a₃a₄ sin А,) + +402 (a,a₂⁰⁰⁸ А+^a3°4 ^cos A,) + +0₂ (-2ao + 2a,² + a² + a₄ ) - 2£²a₄ + +—(aoa₄sinA, + 2а,^а₄ sin(A, -A))- ^аз^{х                                 1}

-—(oqO₄ cos A, + 2a,a₂a₄ cos(A - Д,))ч

+—(ода3 sin A, + 2a,a2a3 sin(A, - A))-#4

-—(2aia₃ + Oga₃ cos A, +2a,a₂a₃ cos(A, - A)j. (14)

Из уравнения (1) выведена система дифференциальных уравнений для амплитуд a_b i = 0,4 и сдвигов фаз волн А, А, (8)-(14), или в векторной форме:

(!5)

где х = [а₀ а, а₂ а₃ а₄ А А,]^г.

Коэффициенты системы (8)—(14) у, di, d₂, а,, а₂, а₃, а₄, 0, (рис. 6), 0₂ (рис. 7) зависят от физикохимических факторов (N, т, а, М).

Рассчитаем область неустойчивости жидкой пленки в рамках нелинейного приближения. Для этого исследуем неустойчивость системы (15) относительно амплитуд a_b z = 0,4.

Перейдем к уравнениям первого приближения для системы (15):

^ = М                   (16)

где у - вектор вариаций неизвестных системы (15), ->=|(й/г^Щ, УМ-

Запишем, х = [y^r z^r]^r, где у = [а₀ «1 «г «з «4]^г -вектор переменных, относительно которых исследуется неустойчивость жидкой пленки, вектор «контролируемых» переменных; z = [Д Ai]^r - вектор «неконтролируемых» переменных.

Тогда (16) представим в виде

[у, = Ay, + Bz

Г4 5    $                         (17)

[^ = Cy$+Dz$, где А, В, С, D - соответствующие подматрицы матрицы J; у», z$ - векторы вариаций «контролируемых» и «неконтролируемых» переменных соответственно.

Для системы (17) можно показать, что:

• 1.    В»0.

• 2.    Для неравенства |R(y„z,^ < ф|_у=0, где R(y_$, Zj) - остаточный член разложения вектор-функции F(x) в ряд Тейлора в окрестности точки

V = 0, справедлива оценка ^ ~ I sup <  a, |_v=0 И •

В таком случае из обобщенной теоремы Ляпунова об устойчивости по первому приближению [8] следует, что для устойчивости возмущений, развивающихся на свободной поверхности тонкого слоя вязкой жидкости, относительно амплитуд а, необходимо и достаточно, чтобы все собственные числа подматрицы А системы (17) имели отрицательные вещественные части. Если среди собственных чисел подматрицы А найдется хотя бы одно с положительной вещественной частью, то возмущения на свободной поверхности жидкой пленки будут неустойчивыми относительно амплитуд а_ь

Спектр подматрицы А исследуем с помощью критерия Зубова [9]: для того чтобы все собственные числа подматрицы А имели отрицательную вещественную часть, необходимо и достаточно выполнения условия Нт £2" = 0, где п - целое Л->00

число, £2 - функционально-преобразованная матрица, £2 = Е-2(Е-А)^-1.

Для исследования неустойчивости возмущений на поверхности жидкой пленки в рамках критерия Зубова реализован алгоритм [11], в котором использованы достаточные формы критерия Зубова [10]. Чтобы вещественные части собственных чисел подматрицы А были отрицательными, достаточно, чтобы, начиная с некоторого £, выполнялось условие м<1.                      (18)

С другой стороны, если, начиная с некоторого £, справедливо неравенство

ISpfi^no,                        (19)

где и0 - порядок подматрицы А (и0 = 5), то среди собственных чисел подматрицы А найдется хотя бы одно с положительной вещественной частью.

На каждом этапе алгоритма анализируется выполнение достаточных условий критерия Зубова (18)—(19). Если выполняется какое-либо из условий (18)—(19), то возмущения в точке плоскости параметров (Ле, к) признаются, соответственно, устойчивыми или неустойчивыми.

Алгоритм реализован таким образом, чтобы осуществлялся анализ выполнения условий (18)(19) для последовательности матриц £2, £22, £24, £216, £232 и т.д. Это дает возможность за сравнительно небольшое число шагов осуществить анализ высоких степеней матрицы £2, поскольку на v этапе алгоритма анализируется 2у~'-я степень £2.

Если за заранее заданное число этапов У т„ добиться выполнения условия (18) или (19) не удается, то в возмущения в точке плоскости параметров (Re, к) считаются неустойчивыми. Такая ситуация возможна, если максимальное число этапов алгоритма задано неверно и необходимо увеличить число v_max, чтобы проанализировать выполнение условий (18)—(19) для еще более высоких степеней матрицы £2. Если матрица Е-А оказывается вырожденной, т.е. осуществить расчет матрицы £2 невозможно, то возмущения также считаются неустойчивыми.

Алгоритм позволяет рассчитать кривую нейтральной устойчивости в плоскости параметров (Re, к) в рамках системы дифференциальных уравнений (15).

Если в плоскости параметров (Re, к) ввести сетку с шагом h по диапазону волновых чисел к, то алгоритм обеспечит расчет кривой нейтральной устойчивости с абсолютной погрешностью 8 < й/2. Для расчета кривой нейтральной устойчивости с абсолютной погрешностью е₀ в диапазоне волновых чисел к е Г ^т™ ; ^ „1 необходимо ввести сетку с числом узлов No = (к^ - А_пйп)/(2е₀).

Вычислительный эксперимент по исследованию неустойчивости жидкой пленки осуществлен для воды (т = 0, М = 0, N = 0), рассчитана область неустойчивости тонкого слоя вязкой жидкости (Re< 12): N_o = 100, к е [0; 0,3], е < 0,0015, v_max = = 20.

Анализ результатов эксперимента (рис. 8 -вершина «треугольника» направлена в область неустойчивых возмущений) показал, что течение жидкой пленки неустойчиво во всем диапазоне чисел Рейнольдса Re < 12. Чем больше значение числа Рейнольдса Re, тем шире зона неустойчивости по диапазону волновых чисел к.

Области неустойчивости жидкой пленки, рассчитанные в линейном (рис. 5) и нелинейном (рис. 8) приближениях, согласуются между собой, рассогласование в вычислениях Nk не превышает 6 % (табл. 2).

Таблица 2

Сравнение расчетов областей неустойчивости в линейном и нелинейном приближениях

Re	Кривая нейтральной устойчивости		ДА, %
	Линейное приближение	Нелинейное приближение
1	0,02714	0,02559	5,71
5	0,10378	0,10357	0,20
7	0,13737	0,13655	0,60
9	0,16937	0,16954	0,10
10	0,18491	0,18454	0,20
12	0,21525	0,21453	0,33

Поскольку в результате волнового взаимодействия на свободной поверхности тонкого слоя вязкой жидкости происходит обмен и перераспределение энергии между возмущениями [7], интересным представляет исследование поведения составляющих амплитуды А(х, z, t) (7).

Для изучения эволюции во времени амплитуд а, волнового возмущения (7) система дифференциальных уравнений (8)-(14) решалась методом Рунге-Кутты 4-го порядка. Изучение осуществлялось в окрестности кривой нейтральной устойчивости.

Исследование показало, что по всему диапазону чисел Рейнольдса Re в окрестности кривой нейтральной устойчивости наблюдается рост амплитуды несущей волны а₀ (рис. 9) и амплитуд наклонных волн а₃, а₄. Амплитуды боковых волн ai (рис. 10) и а₂ вблизи границы области неустойчивости затухают.

С увеличением числа Рейнольдса Re увеличивается скорость роста амплитуды несущей волны а₀ (рис. 9) и амплитуд наклонных волн а₃, а₄; увеличиваются скорости затухания амплитуд а₃, сц (рис. 10).

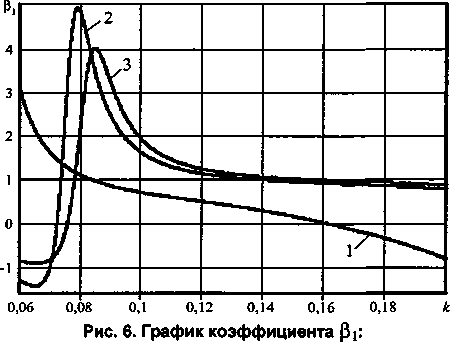
1 -Re = 5;

2-Ле = 9;

3-Re = 10

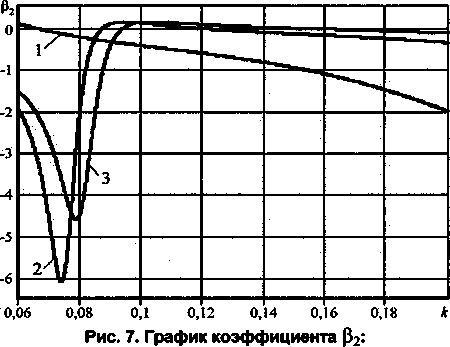
1 -Re = 5;

2-Re = 9;

3-Re=10

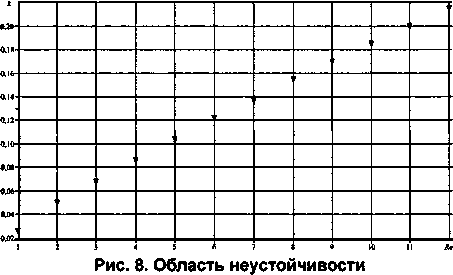
в нелинейном приближении

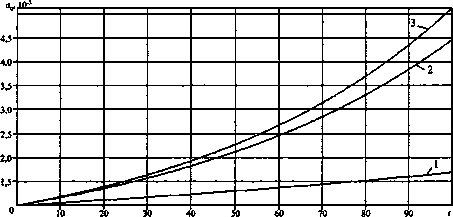
Рис. 9. Поведение а0 в окрестности кривой нейтральной устойчивости: 1-7?е = 5;

2-7?е = 9;

3-Re = 10

Заключение

Исследование неустойчивости жидких пленок, подробное изучение процессов, протекающих на поверхности раздела газ-жидкость, актуально, так как имеет большое научное и прикладное значение.

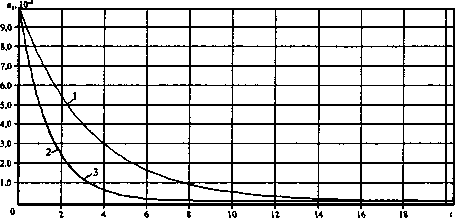
Рис. 10. Поведение а^ в окрестности кривой нейтральной устойчивости:

1 -Re = 5;

2-7?е = 9;

3-Re = 10

Математическое моделирование течений тонких слоев вязких жидкостей дает возможность изучить влияние на них различных физикохимических факторов, что открывает возможности для управления технологическими системами, которые включают пленочные аппараты, для совершенствования методов проектирования и конструирования таких систем.

В рамках математической модели неустойчивых режимов течения жидких пленок, представленной дифференциальным уравнением (1), осуществлено исследование неустойчивости тонкого слоя вязкой жидкости для диапазона чисел Рейнольдса Re < 12 в линейном и нелинейном приближениях, проведен вычислительный эксперимент для воды (т = О, N= О, М = 0).

В линейном приближении получено дисперсионное уравнение (2), выведены аналитические зависимости волновых характеристик (<в„ со,, С, Сгр) от физико-химических факторов (N, т, о, М), рассчитана область неустойчивости (рис. 5) в плоскости параметров (Re, А). Показано, что течение жидкой пленки (воды) неустойчиво в диапазоне чисел Рейнольдса Re < 12, причем зона неустойчивости расширяется по диапазону волновых чисел к с увеличением значений числа Рейнольдса Re. При этом увеличивается скорость роста волновых возмущений (рис. 2), уменьшаются фазовые (рис. 3) и групповые (рис. 4) скорости.

В нелинейном приближении в рамках системы дифференциальных уравнений (8-14) предложен алгоритм расчета области неустойчивости жидкой пленки. С помощью алгоритма вычислена кривая нейтральной устойчивости (рис. 8) для воды (т = 0, N = 0, М = 0). При этом рассогласование между результатами, полученными в линейном и нелинейном приближениях, не превышает 6% (табл. 2).

В рамках нелинейного приближения в окрестности кривой нейтральной устойчивости изучена эволюция во времени амплитуд составляющих возмущения (7). Показано, что по всему диапазону чисел Рейнольдса Re наблюдается рост амплитуд а₀, «з, «4 и затухание амплитуд а^ а₂.