Математическое моделирование обработки расплава порошковой проволокой

В последние десятилетия произошли существенные изменения в мировом и российском сталеплавильном производстве, вызванные созданием разных методов внепечной обработки стали с использованием комплексных агрегатов и технологических процессов, которые обеспечивают улучшение качества стали [1].

Практика показала экономическую и технологическую целесообразность использования порошковой проволоки для микролегирования, легирования и корректировки химического состава стали.

Использование порошковой проволоки имеет следующие преимущества: не увеличивается содержание азота, кислорода и водорода в стали; обеспечивается высокая степень и стабильность усвоения элементов, особенно высокоактивных, например, кальция; в меньшей степени снижается температура металла; не требуется больших капитальных затрат на оборудование; низки эксплуатационные расходы; отсутствуют проблемы с хранением и транспортировкой гидрофильных, легко-окисляющихся, ядовитых и пожароопасных реагентов; обеспечивается возможность введения легирующих добавок в ковш любой емкости, в промежуточный ковш МНЛЗ и в изложницу. Этот метод универсален и позволяет иметь в проволоке практически любые легирующие компоненты по желанию потребителя [2].

Проволока вводится в ковш с расплавленной сталью с определенной скоростью, после чего плавится ее оболочка и расплавляется содержимое. Процесс модифицирования стали определяется скоростью усвоения порошковой проволоки, а следовательно, и скоростью ввода её в расплав. Подобная задача рассматривалась в работе [3], в которой было принято, что движение проволоки происходит в «турбулентном режиме».

В данной работе предлагается математическая модель теплофизики этого процесса, в которой скорость ввода проволоки учитывается в уравнении энергии для движущихся сред [4].

В процессе тепловой обработки расплава участвуют три среды: наполнитель проволоки, оболочка проволоки и расплав в ковше. Так как про- волока имеет цилиндрическую форму, была при- нята цилиндрическая система координат и осесимметричная постановка задачи. Каждая среда имеет свои теплофизические параметры cp, ρ, λ – удельную теплоемкость, плотность, теплопроводность. Поэтому для каждой среды принято уравнение конвективного теплообмена и эти уравнения связаны между собой. Было принято, что теплопередача между средами происходит по линейному закону Ньютона. Первая и вторая среды движутся в поршневом режиме. В геометрическом смысле каждая среда представляет собой слой: наполнитель – цилиндр радиуса R1, оболочка проволоки – коаксиальный цилиндр с радиусами (внутренним R1 и внешним R2) и расплав с радиусом R3. Такая послойная структура системы позволяет учесть радиальную теплопередачу между средами-слоями. Для уменьшения дальнейших вычислительных трудностей приняли, что теплофизические пара- метры сред не зависят от температуры.

С учетом принятых допущений уравнения сохранения энергии для послойной системы сред примут вид:

0 t1        0 L , xx

+ ^W 1"T" ^-K 11 ( t i - t i ) ^{+ K} 12 ( t 2 - t i ) ⁺

0т

<

< x0

^{+ K} 13 ( t 3 - t 1 ) ^{+ a}1”T^; 0 z

0t2

—— + w 2 —— - ^K 21 ( t 1 ^- t 2 ) + ^K 22 ( t 2 ^- t 2 ) +

0T              Я2

0 t ₂

+ K23(t3   t2) + a2

0 z

0t3 .      0t3.

— + ^w3 — = ^K 31 ( t i - t 3 ) ^{+ K} 32 ( t 2 - t 3 ) ⁺ 0т 0 z

,      „         ,0

+ K33(t3 t3) + a32

0z где ti – температура, индексы i = 1, 2, 3 относятся соответственно к наполнителю, стальной оболочке порошковой проволоки и металлическому расплаву в ковше; wi – скорости движения сред; τ – координата по оси времени; z – координата по оси расстояния oz; k^ —a.jjpjj]cipS , ay - коэффициент теплопередачи от i-й среды к j-й, pij – периметр сечения раздела сред, ci, – удельная теплоемкость, ρi – плотность, Si – поперечное сечение i-й среды; ai – температуропроводность.

Уравнения (1) дополняются начальными и граничными условиями:

t i (z ,0) = t H (z ), i = 1, 2, 3;

k t = а з [ 1 3 (0, T ) - t i (0, T )], i = 1, 2,3.

оz

Системы уравнений (1), (2) записаны в симметричном виде. Для рассматриваемого процесса обработки расплава приняты следующие допуще- ния:

• •    w 1 = w ₂, w ₃ = 0 - наполнитель не перемещается внутри оболочки, вся порошковая проволока погружается в неподвижный расплав;

• •    a 1 = a ₃ = 0 - для порошка и для расплава

гаемых в уравнениях (3), описывающих радиаль- ную теплопередачу.

Для численного решения смешанной задачи (1), (2) использовали метод конечных разностей. Решение уравнений (1), (2) в области D заменили решением в точках разностной сетки D .

В качестве сетки D ввели совокупность точек пересечения прямых z = m Δ z и τ = n Δτ в области D , где m = 0, 1, …, M ; n = 0, 1, …, N ; Δ z = l ; Δτ = h ; l >  0, h >  0 .

После замены частных производных их разностными аналогами в уравнениях (1) и (2) и необходимых преобразований получено итерацион- ное матричное уравнение:

t^ m , n + 1 = pt m - 1, n । Qt^m , n । Rt ^m + 1, n

где tm,n = t(ml, nh), tm-1n = t((m -1)l, nh), не рассматривается температуропроводность по

длине;

t ^m + 1,n = t (( m + 1) l , nh ), t ^m , ^{n +1} = t ( ml ,( n + 1) h ) -

• к ii = 0 - коэффициент теплопередачи a и внутри среды принимается равным 0.

Введем вектор-функцию t = [ t ₁ t ₂ t ₃] ^T , тогда

значения вектор-функции в узлах сетки;

уравнения (1) запишутся в виде:

hh

P = — A + — W ;

l 2       2 l

где

8t   ... дt            . д ² t

— + W — = Kt + A—-, дz z

дт

дz

2 h

Q = hK —2~ A + E;

W =

w ₁ 0

00 w 2 0 0 w ₃

R = ^A - — W ; l ²      2 l

Е – единичная матрица.

Граничные условия запишутся следующим образом:

^ j = 1 ^к 1 j

K =	к 21
	_   к 31

^к 12

Л j=1к2 j к32

^к 13

^к 23

^ j = 1 ^к 3 j

— Л ( 1 2, ⁿ - 1 0, ⁿ ) = a ( 1 1, ⁿ -0 ¹);

^{2 l}                                                (5)

—Л ( t k ⁺ 1, ⁿ - t k ^- 1, ⁿ ) = a ( t k , ⁿ -0 k ),

A =

a ₁ 0

00 a 2 0 0 a ₃

	Х1	0	0 "		a 12	0	0 "
где Л =	0	х 2	0	, a =	0	a 23	0
	0	0	^ 3 _		0	0	a 32 _

При рассмотренной постановке задачи теплового взаимодействия порошковой проволоки, движущейся со скоростью w в расплаве, учтен главный фактор – динамика движения проволоки в расплаве. При погружении проволоки в расплав происходит ее нагрев и на какой-то глубине плавление оболочки. В работах [1–3] использовали статические уравнения теплопроводности, не содержащие конвективного члена, то есть фактически не учитывали скорость движения проволоки и рассматривали теплообмен только в радиальном направлении, что не соответствует действительному процессу. При постановке задачи в данной работе заведомо пренебрегли радиальными тепловыми эффектами, приводящими к появлению корочки на оболочке, или так называемыми эффектами на подвижной границе, описываемыми уравнением Стефана. Учет этих эффектов потребовал бы введения координаты r и, соответственно, сла-

	1 2, n		1 2k , n
0 1 =	1 3, n	, 0 k =	1 3k , n
	_ t 2, n _		k , n L t 2 J

Из граничных условий выразим t ^{0, n} и t ^{k+ 1, n} (соот-

ветственно температуры на 0 и k +1 шагах по длине) и подставим эти параметры в уравнение (4). После преобразований получим уравнение в виде:

^m , n + 1	= Mt	m , n	+ N ,				(6)
	" Q 1	R 1	0			0 "
	p 2	Q 2	R 2	0		0
где M =	0	P 3	Q 3	R 3		0	;
	0		0	P k -1	Q k -1	R k -1
	L 0			0	P k	Q k _

Исходные данные расчета

Среды	Геометрия			Теплофизика					Параметры моделирования и начальные условия
	R , м	S , м2	p , м	a , м2/с	c , Дж/ (кг∙К)	ρ, кг/м3	λ, Вт/ (м∙К)	α, м2/с	h , с	l , м	w , м/с	t н, К
Наполнитель	0,005	7,9∙10–5	0	0	705	2326	0,75	0	1∙10–4	0,2	5	293
			0, 0 31 4					5∙103
			0					0
Оболочка	0,0052	6,4∙10–6	0, 0 31 4	1∙10–5	840	7200	47	5∙103			5	293
			0					0
			0,033					35∙103
Расплав	0,5052	8,0∙10–1	0	0	840	7200	47	0			0	1873
			0,033					35∙103
			0					0

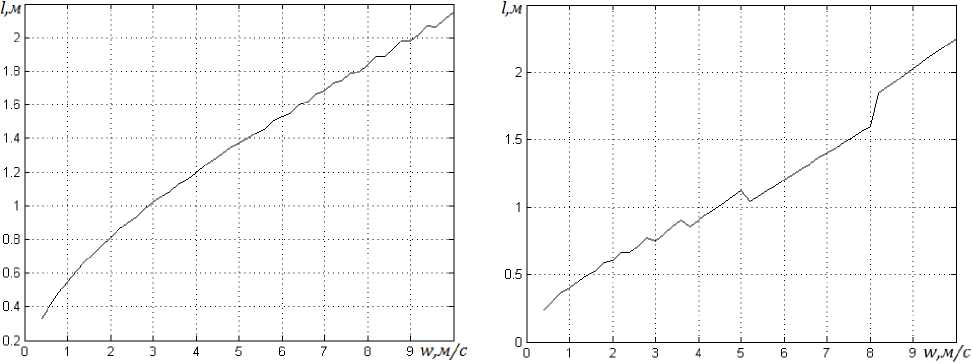
а)                                                                     б)

Рис. 3. Зависимость глубины погружения от скорости ввода: а – при h = 5∙10^–4 с и l = 5∙10^–2 м; б – при h = 2,5∙10^–3 с и l = 2,5∙10^–2 м

1400 -•••

1600 F--

800 ----

1200 к --

600 к -

----- Наполнитель --Оболочка --- Расплав

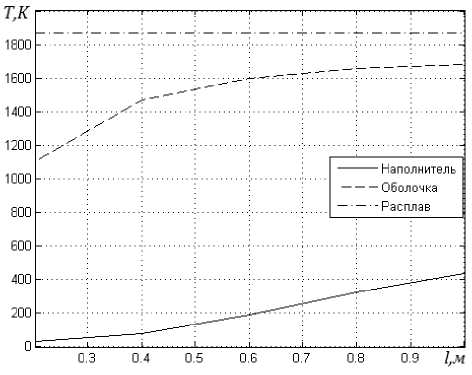
Рис. 2. Распределение температур сред при t = 0,2 c и скорости ввода проволоки 5 м/с

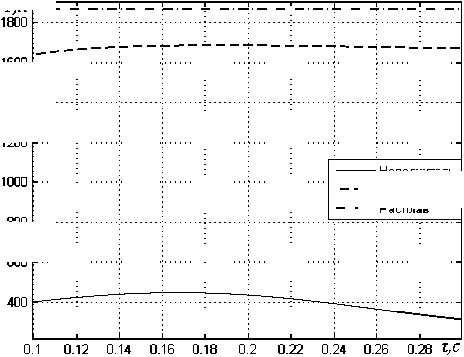
Рис. 1. Зависимости температуры сред от времени при z = 0,5 м и скорости ввода проволоки 5 м/с

	■ PH 0 1 "  0
N =	... 0 -RH 0 k _	; Q 1 = Q - PH ; R 1 = P + R

P^k = P + R ; Q ^k = Q + RH ; H = 2 1 ■Л ^-1 а .

В качестве наполнителя при расчёте был выбран силикокальций, так как примерно 60 % порошковой проволоки в мире производится с этим компонентом.

Результаты численных расчетов рассматриваемой краевой задачи на примере силикокальция приведены на рис. 1–3. Теплофизические свойства сред были приняты такими же, как в [3]. Исходные данные для расчета приведены в таблице.

Полученные результаты моделирования процесса обработки расплава методом скоростного ввода порошковой проволоки показали, что зависимость глубины погружения проволоки от скорости ввода имеет не апериодический характер. Это объясняется многими факторами:

• •    высокоинтенсивный процесс теплообмена описывается гиперболической системой уравнений (1), решение которых может иметь колебательный характер;

• •    параметрами разностной сетки;

• •    параметрами сред.

На рис. 1, 2 приведены некоторые результаты расчета температурных полей по средам. На рис. 3 приведены зависимости глубины погружения проволоки до начала плавления оболочки от скорости ввода. Можно заключить, что процесс теплообме- на проволоки и расплава имеет нелинейный характер. По полученной модели можно определить оптимальную скорость ввода проволоки, при которой плавление начинается на необходимой глубине.

Таким образом, разработана универсальная математическая модель, с помощью которой можно анализировать тепловые процессы, происходящие при легировании, модифицировании и раскислении стали порошковой проволокой с различными видами компонентов в ходе внепечной обработки.

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 13-0800638.