Математическое моделирование переходного процесса в выходной цепи управляемого электрохимического сопротивления

Введение. УЭХС представляет собой цилиндрический проводник длиною / прямоугольного сечения (подложка) a х r , изготовленный из стеклографита. Если на боковую поверхность УЭХС наносить электрохимическим способом тонкий слой металла, то сечение слоёного проводника будет увеличиваться, а его сопротивление уменьшаться. Ставится задача получить зависимость выходной величины УЭХС от тока (плотности тока) в цепи управления (рис. 1).

Вывод зависимости R ( t ) от тока управления. Пусть р п и р _м — удельные электрические сопротивления материалов подложки и наносимого осадка металла, S_п и S_м ( x ) — поперечные сечения подложки и осаждённого металла, dR_п — элемент электрохимического сопротивления подложки длиною dx , dR_м — элемент электрического сопротивления осаждённого металла дли-

ною dx . Тогда

р„ dx dRn = П ,                                           (1) Sп р dx dR = мл . м   S м ( x )                                              (2)

Параллельное включение этих элементов приводит к такому эквиваленту

dR ■ dR dR =--- п-----«. . dR n + dR »

Подставим (1) и (2) в (3)

P n dx р M dx    р n   р м

------------------------ ■----------------------------- ------------- ■ ----------------------------- dR = -S---SM (x) = Sn SM (x) dx =----------dx.                  (4)

P n dx , p M dx    P n , P м        P п 5 м ( x) + P м⁵п

S п    S м ( x )   S п S м ( x )

Как видно из полученной формулы, дальнейшее исследование сводится к получению зависимости S м ( x ).

Пусть δ(x;t) — известное пространственно-временное распределение плотности элек- трического тока на управляющем электроде. Тогда 5(x;t) ■ a ■ dx — ток управления в момент t

t через площадку a ■ dx . J 5(x; t)a ■ dx ■ dt — заряд, прошедший через площадку a ■ dx за отрезок 0

времени [ 0; t ] .

Если к — электрохимический эквивалент осаждаемого металла, то [ 1 ]

t dm = кJs(x; t)a ■ dx ■ dt — масса осаждённого металла на площадке a ■ dx , за отрезок времени 0

[ °: t ] .

k [ 5 ( x ; t)a ■ dx ■ dt

—

Если ум — объёмная плотность осаждённого металла, то dVM = — = —------------- Y м             Y м объём осаждённого металла на площадке a ■ dx за отрезок времени [0; t].

Считая форму осаждённого металла на поверхности бесконечно малой площади a ■ dx в виде параллепипеда, можно найти площадь поперечного сечения S_м ( x ) в точке x :

t ka J5(x;t )dt

.

Sm (x) = V, или Sm (x) =   -------- dx                    Y м

Подставим (5) в (4)

dR =---- t--^------- dx .

ka J s ( x ; t )dt                                                  (6)

P n —-------- ⁺ P м ■ ^Sn

Y м

Выходная величина УЭХС легко может быть рассчитана с помощью интегрирования выражения (6) по x :

R(t ) = J------ t---------------- dx .

°     ka J 5 ( x ; t )dt                                                 (7)

P n —-------- ⁺ P м ■ ^Sn

Y м

Полученная формула (7) может быть использована при произвольном распределении плотности тока 5 ( x ; t ) в цепи управляющего электрода, в том числе и при равномерном, когда

5 ( x ; t ) =

I y ( t )

У ■ a '

где I_y ( t ) — ток управления.

Подставляя (8) в (7) получаем

R(t) =-----1 P п Р мм-------- k J Iy (t )dt

^Р п _Y . £   ^{+ Р M}Sⁿ

м

При постоянном токе управления I y (t ) = I _o = const формула (9) ещё более упрощается:

Р п Р м*

kIt    е

^Р п   7 ^{+ P} M S n

Y М ^£

Зависимость R ( t ) в соответствии с формулой (10) принимает гиперболический характер (рис. 2).

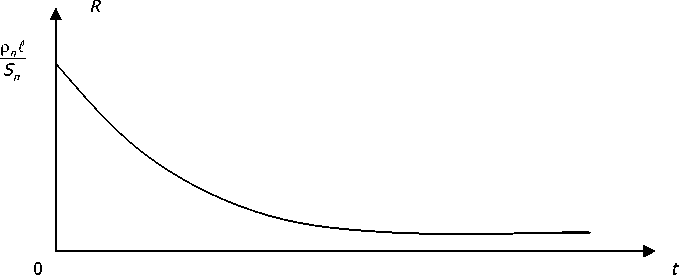
Рис. 2. Зависимость R (t) от времени при I_y(t ) = I, = const

Далее при расчётах переходных процессов в схемах, содержащих УЭХС, будем считать, что распределение плотности тока в цепи управляющего электрода является равномерным, т. е. будет использоваться формула (9).

Математическое моделирование переходных процессов. Второй закон Кирхгофа для приведённой на рис. 3 схемы имеет вид

i(t)R(t ) + i(t)R„ + L „ dit = E „ . dt

Разрешая уравнение (11) относительно производной, получаем di E о - i ( t ) ( R ( t ) + R o ) dt⁼                     '

По первому закону коммутации для данной цепи [ 2 ] i (0 - 0) = i (0 + 0) = 0, т. е.

i (0) = 0

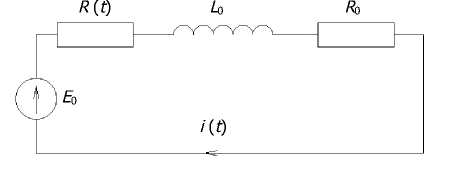
Рис. 3. Включение R ( t ) с активно-индуктивной нагрузкой

Задача коши (12), (13) легко может быть решена численно одним из известных методов, например, методом Эйлера.

Введём в рассмотрение функцию

f (R (t); i (t ))*

e о - i ( t ) ( R ( t ) + R )

L 0

Пусть tmax — время переходного процесса, n — количество дискретных временных точек переходного процесса. Тогда временной шаг определяется соотношением h = tmax.                                               (15)

n

Итерационная формула Эйлера для массива тока {ij ;j = 0, n} имеет вид ij+1 = ij + hf (Rj; ij),                                                (16)

где R j = R ( t j ) , i j = i ( t j ) .

Алгоритм расчёта переходного процесса в схеме, изображённой на рис. 3, можно представить следующей блок-схемой (рис. 4).

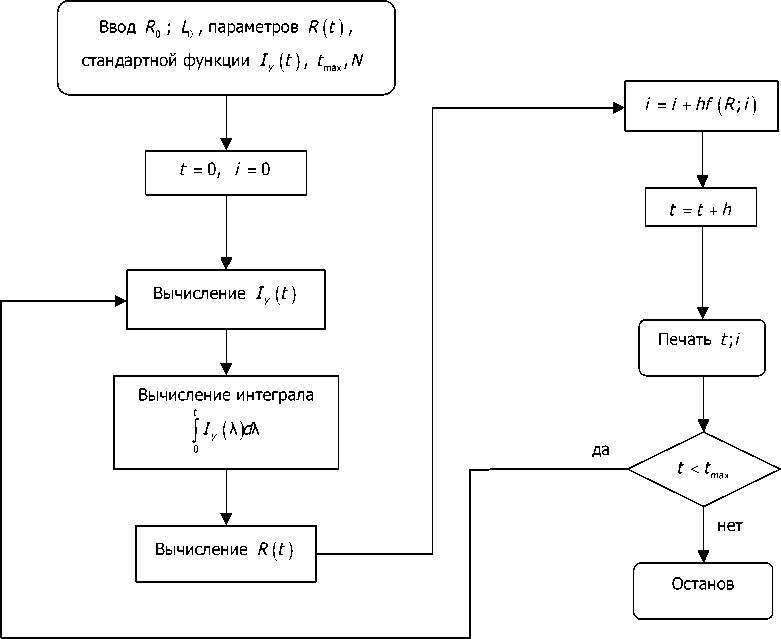
Рис. 4. Алгоритм расчёта переходного процесса в цепи R ( t ) - R ₀ - L

При исходных данных E _о = 2 B ; р п = 8 ■ 10 ^{- 5} Ом ■ м ; S_n = 10 ■ 10 ^{- 6} м 2 ; р _м = 1,72 ■ 10 — 8 Ом ■ м ; к = 0,6588 ■ 10 ^{- 6} кг / Кл; I = 0,10 м ; I _о = 0,1 Л ; у _м = 8,9 ■ 10 3 кг / м 3 ; R _o = 5 Ом ; L = 0,1гн была рассчитана зависимость i ( t ) , представленная на рис. 5.

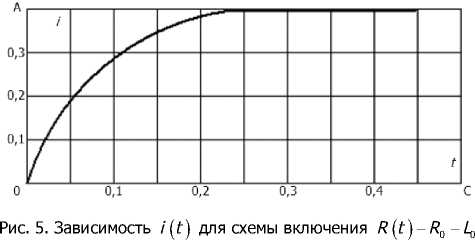
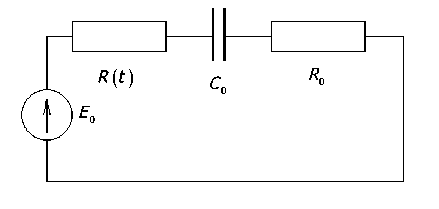
Рис. 6. Включение R ( t ) с активно-ёмкостной нагрузкой

Второй закон Кирхгофа для приведённой на рис. 6 схемы имеет вид

t i (t)R (t) + i (t)R + -1 Ji (t)dt = Eo.                                  (17)

с _{0 0}

Для получения дифференциального уравнения относительно i ( t ) продифференцируем (17) по t .

di           dR ( t )      di 1

— R ( t ) + i ( t )—— + R — + — i ( t ), dt            dt ° dt С

O откуда

±+dR (t)

di       С 0     dt

dt      ⁽ t ) R ( t ) + R 0 '

где

^dR ( t )

dt определяется при дифференцировании (9).

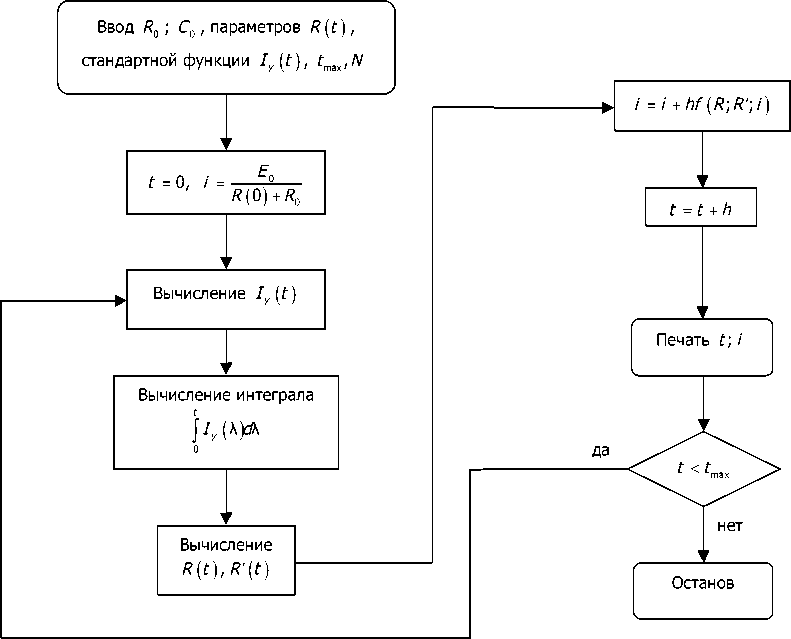
Рис. 7. Алгоритм расчёта переходного процесса в цепи R ( t ) - R 0 - С 0

р П р м^к

dR dt

—

Y м

Iy (t )

г. t                          ^.

| ^P4j l y ( t ) dt + P m S „ I ^y

V ^Y м о                        7

По второму закону для схемы на рис. 6 можно записать

U c 0 ( ⁰ — ⁰ ) = U c 0 ( ⁰ + ⁰ ) = ⁰, откуда получаем при t = ( 0 + 0 )

i (0)R (0) + i (0)Ro = Eo, т. е.

i (0) = —E---.

( ) R (0) + Ro

Таким образом, расчёт переходного процесса для i ( t ) в схеме на рис. 6 сводится к решению задачи Коши (18), (20).

Введём в рассмотрение функцию f IR (t); dR; i (t T—i (t)

±+dR (t)

C 0    dt

R ( t ) + R o .

Итерационная формула Эйлера для массива тока {ij; j = 0, n} имеет вид ij. = ij + h (Rj; Rj; ij), где

R j = ^R ( t j ) - i j = i ( t j ) , ^Rj =

^dR ( t j )

dt

.

Алгоритм расчёта переходного процесса в схеме, изображённой на рис. 6, можно представить следующей блок-схемой (рис. 7).

При E _o = 2B;R _o = 5Ом; С_ = 0,005 ф была рассчитана зависимость тока i ( t ) (рис. 8) в схеме, представленной на рис. 6.

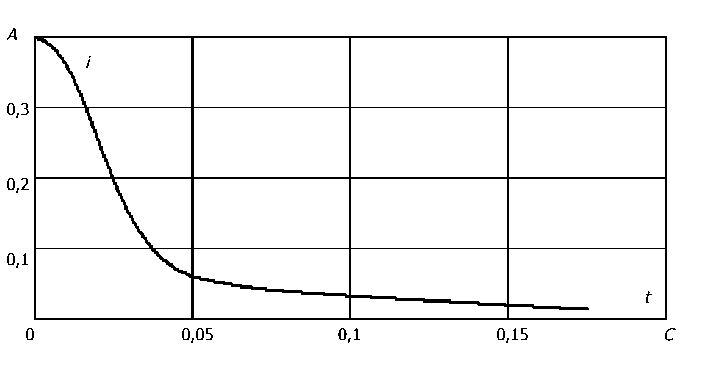
Рис. 8. Зависимость тока i ( t ) для схемы включения R ( t ) — R ₀ — С ₀

Заключение. Полученная математическая модель УЭХС успешно может быть использована для расчёта переходных процессов в линейных и нелинейных схемах, содержащих этот элемент. В большинстве случаев, даже для линейных схем, эта задача решается только численно.