Математическое моделирование пластической деформации скольжением в Г.Ц.К. сплавах с некогерентной упрочняющей фазой

¹ U i. ^- A

^{d р} Р ^- = 8 da 2 A ² _p b

_р'/У Р - b V D a

k

^Z~_l ^ex P k

kT k kT J

I U im ) J

k kT J

+ Z v c v exP

+ 2 Z v C v exP

¹ U vm ) J

k

kT J

U v m ^- )

k kT J

+ Z 2 v c 2 v exP

k

+ 2 Z 2 v C 2 v exP

( m )

^U 2 v’

kT

( m U 2 v

k kT

, (8)

Уравнения баланса дислокаций в дипольных конфигурациях. Считая, что образование дислокаций в дипольных конфигурациях межузельного и вакансионного типа равновероятно, можем оценить их генерацию соответственно как [7]

G_dl ( р ) = G_dv ( р ) = ( Л p b ) - ¹.

Процессы аннигиляции диполей рассмотрим аналогично

процессам

аннигиляции и диффузионного роста призматических петель [7, 13]. Используем предположение, что распределение диполей по длине плеча является равномерным на интервале [ y min , y max ], и будем считать, что максимальное плечо диполя, после достижения которого он теряет свою устойчивость, равно критическому радиусу захвата y max =r a , и y min =0. Уравнения баланса дислокаций в дипольных конфигурациях имеем в виде [13]

d ^ d )_   1

da

^Л p^b   a & ^Ь У max

р ⁾ ь ²v d

^{Zc ex}P

/ U m

d р ^ ^- da

^ P^Ь 2 ^V D

k

Z i c i ^ex P

k

k

kT J

U i m ^- A

Z vcv eXP

U m ^- A

k kT )

Z vcv eXP

k kT J

1 U ( m ) J

^{+ Z} 2 v c 2 v exP

( m )

_ ^U 2 v

k

kT

, (11)

k kT )

⁺ Z 2 _v ^c 2 v exP

( m U _{2 v}

k kT

Скорость деформации скольжением в гетерофазных материалах

Уравнение для скорости деформации связывает переменные, характеризующие деформирующее воздействие и деформационную дефектную подсистему кристаллического тела, с количественной характеристикой отклика материала на деформирующее воздействие скоростью деформации [4- 6, 11, 13, 15]. В работах [5-7, 12] показано, что даже в условиях статической деформации зона сдвига формируется преимущественно в динамическом режиме в условиях потери устойчивости дислокационными конфигурациями. В широком интервале условий квазистатической деформации время достижения дислокационным сегментом-источником критической конфигурации существенно превышает время дальнейшего движения дислокации до границы зоны сдвига [16]. Уравнение для скорости деформации скольжением в условиях статической деформации, записанное в предположении термоактивируемого движения дислокационного сегмента-источника до достижения критической конфигурации, которое сменяется динамическим движением дислокаций после её преодоления, имеет вид [11, 13, 15]:

8 ^е r ^1/2 Р m ^{1/2 V} D b ^2/3 D ⁽(0 -P r ) P m ⁺ P P ⁺ P d ^{)( т - т} a )F Г U ^{- ( т - т} a ^{) Л} b b n F ^/6(1 -P r ) G ^1/3                     [ kT

. (13)

Здесь £ - доля дислокаций леса, вr - доля реагирующих дислокаций леса, ar - параметр междислокационных взаимодействий с реагирующими дислокациями леса, т a - атермическая составляющая сопротивления движению скользящей дислокации, Л определяется выражением [1, 2]:

Л = ^

(^ a Р ^3/2 ) ' 3

rr _m

+

1 / 3

ЭД1 -Р r )р m + Р p + Р d )(т-т a )

^f 1

k¹ / 3 1

- 1

Gb

k

+ Л2 (Л k p( p

-5) J

>

Принимая [7] для дисперсно-упрочненных материалов т = т у +т Or +a Gb р ^1/2, т Or = Gb ( Л _p -5 ) ^{- 1} - сопротивление движению дислокаций, связанное с накоплением геометрически необходимых дислокаций на частицах, можно записать т _a =т f + Gb ( Л _p -5 ) ^{- 1} +a _aGb р ^1/2 .; U = 0.2Gb³, v = v d b /Л [4, 7] .

Таким образом, математическая модель пластической деформации гетерофазных материалов с некогерентной упрочняющей фазой включает уравнения (2)–(4), (7)–(9), (11)–(12), (13). Для проведения вычислительных экспериментов с использованием сформулированной математической модели пластической деформации скольжением в гетерофазных материалах необходимо к рассмотренным уравнениям баланса деформационных дефектов и уравнению для скорости деформации добавить уравнение (либо уравнения), описывающее деформирующее воздействие.

Пластическая деформация скольжением в условиях деформации с постоянной скоростью деформирования

Для пластической деформации в условиях постоянной скорости деформирования используем уравнение, определяющее воздействие на материал, в виде c i = const и T d_yn = a d_yn Gb р ^1/2 [5, 6]. Расчёты проведены для значений параметров, характерных для монокристаллов диспесно-упрочненных сплавов на основе меди [4-7]: b = 2,5 - 10^-10 м^-2, F = 4, v d = 10¹³ c^-1, a = 0,5, a a = 0,45, a r = 0,3, p r = 0,14, ^ = 0,5, т у =10 МПа, v = 1/3, a dyn ~ 0,33, ® ₅ = 0,3, a = 0,01 c ^{- 1} , U{ = 3,28 эВ, U ^ , = 1,27 эВ, U_i ^m =0,117 эВ, U _v ^m = 0,88 эВ.

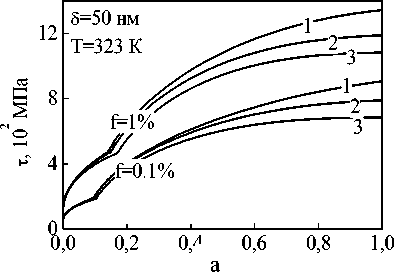
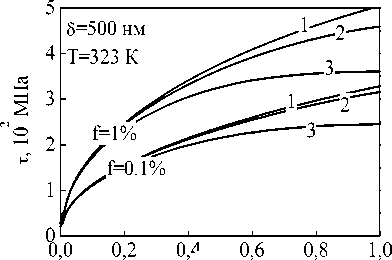
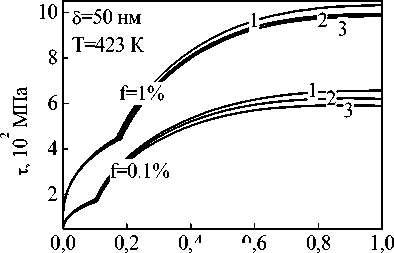
Для деформационного упрочнения гетерофазных сплавов характерно существование двух стадий, разделенных критической плотностью дислокаций и различающихся как характером дислокационной структуры, так и закономерностями пластического поведения (рис. 1, 2). На рис. 2 приведены кривые, отражающие кинетику накопления деформационных дефектов при различных температурах.

При малых размерах частиц сплавы, содержащие частицы второй фазы, характеризуются высоким пределом текучести и высокими скоростями деформационного упрочнения. При диаметре частиц больше 100 нм действующее напряжение мало изменяется с увеличением размеров упрочняющих частиц. С повышением температуры интенсивность деформационного упрочнения уменьшается, и, следовательно, исчезает эффект дисперсного упрочнения. При увеличении объемной доли, а также при уменьшении размеров частиц интенсивность деформационного упрочнения увеличивается. При этом переход из докритической области в закритическую происходит при больших степенях деформации.

в

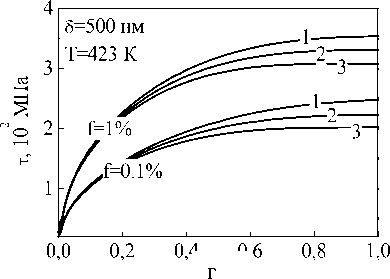
Рис. 1. Зависимость напряжения и коэффициента деформационного упрочнения от степени деформации для дисперсно-упрочненного материала на основе меди при различных скоростях деформирования: 1 – 10-1 с-1, 2 – 10-2 с-1, 3 – 10-4 с-1

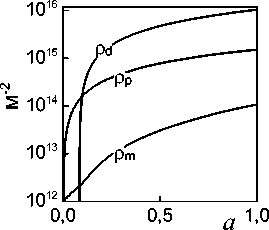
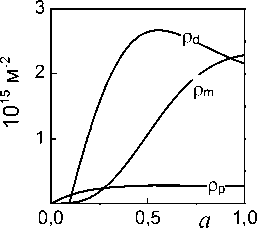
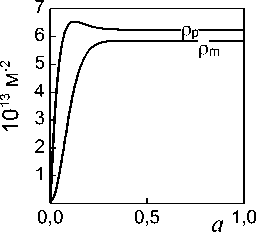
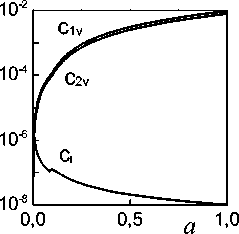
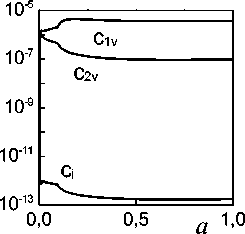
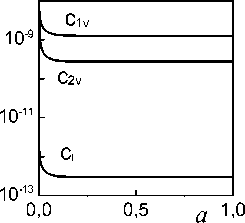
Рис. 2. Зависимость плотности деформационных дефектов различного типа от oo деформации, δ=500 A , Λp=7000 A при температурах: a,г – 77 K, б, д – 473 K, в, е – 873 K

При малой объемной доле частиц процесс деформации происходит полностью в области закритической плотности дислокаций. С увеличением f можно наблюдать две области: докритической плотности дислокаций и закритической. При большой объемной доле частиц (f=20%) процесс деформации происходит в условиях докритической плотности дислокаций. Однако для всех кривых характерна тенденция к насыщению, при этом с увеличением объемной доли частиц предельное значение плотности дислокаций и действующего напряжения увеличивается. В докритической области плотности дислокаций преобладают призматические петли, в закритической – дислокационные диполи (см. рис. 2).

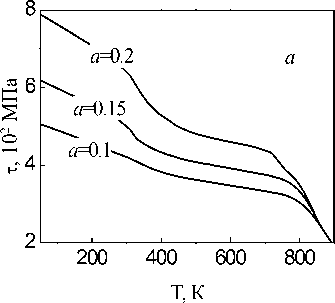
Рис. 3. Температурная зависимость напряжения течения для дисперсно-упрочненного материала на основе меди при δ =50 нм, f =1%. Номер на кривой ( b ) – скорость деформации (с^-1): 1 – 10^-1, 2 – 10^-2, 3 – 10^-3, 4 – 10^-4, а =0,15

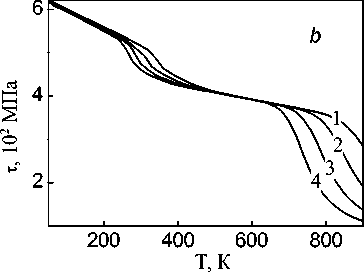
Для температурной зависимости деформирующего напряжения характерно наличие двух интервалов сильной температурной зависимости (рис. 3). Один соответствует интервалу температур, в котором начинается интенсивная аннигиляция дислокаций за счет моно- и бивакансий, второй связан с развитием деформационных процессов, связанных с термодинамическими равновесными точечными дефектами. При этом для низких температур деформирования до 250 К и в интервале температур 400–650 К кривые деформационного упрочнения практически не чувствительны к изменению скорости деформирования (см. рис. 3). Аналогичный характер экспериментальной температурной зависимости при различных скоростях деформации наблюдался для меди, содержащей некогерентные частицы.

Основные полученные закономерности согласуются с экспериментальными данными.