Математическое моделирование подъёма воды в капиллярах, имеющих форму цилиндрической вертикальной спирали

По-видимому, ксилема высших растений не является набором простых вертикальных трубок, по которым движется вода, а представляет собой более сложную структуру, в которой продвижение воды происходит не только прямолинейно. Для понимания этого достаточно посмотреть на многочисленные и многообразные жизненные формы растений.

Стволы многих растений прямолинейны. В отличие от стволов боковые побеги и ветви часто выглядят как разнообразные математические кривые линии. Нелинейность боковых побегов может быть обусловлена воздействием на них ауксина и таких явлений, как отрицательный гравитропизм, фото-, термо- и хемотропизмы . Криволинейные ветви могут иметь самый разный вид. Так, например, ствол фанерофитов [6, стр. 133, рис. 68] вертикален, а боковые ветви напоминают математическую экспоненциальную кривую. Внешне боковые побеги эвгалофита солероса (Salicornia sp.) [7, стр. 242, рис. 231] имеют вид параболических кривых, попарно симметрично отходящих от прямолинейного ствола. Точно так же расположены боковые побеги погремка большого (Rhinanthus major) [7, стр. 260, рис. 246].

Известны также автономные круговые движения растущей вверх верхушки стебля — круговые нутации [8], [9], [10, стр. 408]. Так лиана хмеля (Humulus lupulus), обвивающаяся вокруг опоры, образует цилиндрическую спираль [8, стр. 260, 261, рис. 247]. Гречишка вьюнковая (Polygonum convolvulus), жимолость (Lonicera periclymenum) и вьюнок заборный (Calystegia cepium) тоже всегда обвивают опору, что обеспечивает им рост в форме спирали. У лазящих растений, например у гороха, в цилиндрическую спираль закручиваются усики, а иногда усиком может быть и модифицированная ветка, как у винограда (Vitis vinifera) [8, стр. 225-227].

Работа выполнена в рамках инициативной НИР.

Естественно, что ксилема таких растений (или отдельных их частей) должна быть криволинейна и по виду соответствовать той криволинейной части растения, в которой расположена. Криволинейность ксилемы предполагает пространственную кривизну составляющих её цепочек трахеид и сосудов. Растение или отдельные его части могут иметь форму цилиндрической спирали, обвивающей опору. Но спиралевидный подъём воды иногда имеет место и в прямолинейных стволах. Так, например, в [11] авторы, ссылаясь на сообщение К. Томаса (1967), проводившего исследования по движению воды в кизиле, сообщают, что краска, введённая в ксилему, передвигается по спирали приблизительно на 90° на каждый метр подъёма. В этой же работе приводится утверждение И. Рудинского и Р. Вите (1959) о том, что спиральный подъём ксилемного сока, в отличие от строго вертикального, обеспечивает более равномерное распределение воды по всем частям кроны. Данные выводы основаны на следующем наблюдении. Дуб белый (ксилемный сок передвигается вверх почти вертикально) меньше повреждается от болезни увядания, вызванной сосудистым бактериозом, чем дуб болотный (восходящий транспирационный ток проходит по спирали и расходится в верхней части растения).

Спиралевидное продвижение транспирационного тока свидетельствует о наличии кроме вертикальной ещё и горизонтальной его составляющей. В источниках отсутствуют сведения о расчётах подъёма воды в спиралевидных капиллярах, в том числе применительно к движению воды в растениях. Поэтому стоит задаться вопросом о подъёме воды в капиллярах, имеющих форму цилиндрической спирали, что и является целью данной работы.

Теоретическая модель. Рассмотрим капилляр с внутренним радиусом г, наружным диаметром d_H = 2(г + £) (£ — толщина стенки капилляра). Данный капилляр закручен в виде цилиндрической спирали диаметром De углом подъёма витка, равным р, и шагом б (рис. 1).

Развёртка витка цилиндрической спирали представляет собой прямоугольный треугольник с гипотенузой /_в, катетами D и б, углом р между /_в и D. Учитывая это, длину витка /_в спирали можно определить из соотношения

/в = Vo2+62 = б ч/1 + (ctg₽)2 = D^l + (tgP)2. (1)

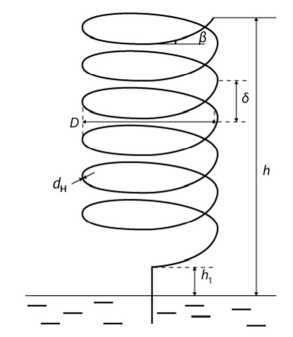
Рис. 1. Капилляр в виде цилиндрической спирали

Из (1) следует, что длина витка спирали увеличивается:

• -    во-первых, прямо пропорционально диаметру спирали,

• -    во-вторых, по мере увеличения угла наклона витка (от его минимально возможного значения Р = arctg (0/2 (г + £)), стремясь к оо при р -> 90°).

Последнее означает, что шаг б между витками спирали стремится к оо, а капилляр становится прямолинейным вертикальным.

В [1] и [2] показано, что величина продвижения воды L в прямолинейном капилляре с внутренним радиусом г, наклонённом к поверхности воды, равна

L = h / sin р

2а cos о rpgsinp

где h — высота подъёма воды в вертикальном капилляре радиуса г, ₽ — угол наклона капилляра к поверхности воды; a — угол смачивания, зависящий от молекулярного взаимодействия на границе раздела трёх сред: стенки капилляра, жидкости и воздуха; о и р — соответственно коэффициент поверхностного натяжения и плотность воды; g — ускорение свободного паде ния.

В случае криволинейного капилляра, имеющего вид у = hi + АУ” (hi — высота прямолинейной вертикальной части капилляра от поверхности воды до начала криволинейного капилляра, АУ” — криволинейная часть капилляра, представляющая параболу степени m с фокусом, равным А), величина продвижения воды равна [4, 5]

L=(h -/7^/(1-cos9),                              (3)

где 0 = arctg km

h - h, m _____L

V k

угол наклона касательной к мениску воды в капилляре к гори

зонтали.

В [1-5] показано, что в общем случае высота подъёма воды в прямолинейных и криволинейных капиллярах не зависит от угла наклона к горизонтали и вида их кривизны и всегда равна высоте подъёма воды h в одиночном вертикальном прямолинейном капилляре равного радиуса. Из этого следует, что количество витков п спирали при заданных значениях d_H, б (hi = 0) не может превышать величины, определяемой соотношением:

/7 = /7 / (гУ/у + б) = /7 / (2(Г + £) + б),(4)

а максимально возможное количество витков в спирали при отсутствии промежутка между ними (б = 0):

/Тмакс = /7 / (2(Г + £)).

При этом угол подъёма спирали минимален и равен

Змии = arctg (2(г + е)/О).(6)

Из (1) и (4) следует, что величина продвижения воды в капилляре в виде цилиндрической спирали определится соотношением

1Ц = шБ = /7o7i + (tg 3)7(2 (г + е) + б)(7)

или

Г>=о77(1д|7/(2(г + Е) + б).(8)

Общее количество витков п, суммарная длина которых равна длине прямолинейного капилляра такого же радиуса:

п = Ц1В =(h-h,)/(/в sinр) = (/7 -hx)ДDsin71 + (tg₽)2^ = (h -hx)/(sin^ЕУ + 62).(9)

Здесь угол подъёма витка спирали ₽ находится в пределах его минимально возможного значения, согласно (6) равного arctg (2(r + е) / D), когда п = /Тмакс, до 90°, когда п^1.

Физический смысл последнего заключается в том, что капиллярная система из спиралевидной превращается в вертикальную прямолинейную, описываемую выражением (2).

Приравнивая выражения (4) и (9), можно записать соотношение:

(fi-W^sin^l + ^gP) J = (/? -/71) / ^ + б).(10)

Откуда минимально возможный диаметр спирали Лин при заданных п, d_H,<5w$ равен:

п            +М 1 >

141ИН — -----,      = .)

sinp^l + (tg₽)2

Из (И) следует, что диаметр витка спирали не зависит от h и п и может принимать любые значения, ограниченные только углом ₽мин.

При 5 = 0 величина D соответствует случаю, когда витки спирали плотно примыкают друг к другу. Следует заметить, что в рассмотренном выше случае максимально плотно витки будут уложены и тогда, когда угол ₽ будет иметь минимально возможное (см. (6)) значение. При этом общая длина спирали максимальна и, следовательно, величина продвижения и количество воды в спирали данного диаметра максимальны.

При л = 1, т. е. когда в спирали присутствует только один виток, его диаметр может быть определён из (9) с учётом (7) в виде

D = ----.                                 (12)

sin₽^l + (tgP)2

В случае, когда 1 < /7 < /Тмакс, диаметр витка может быть определён из (9) и равен

D= -----.                               (13)

nsin₽^l + (tgP)2

Вывод. Полученные результаты показывают, что пространственная спиралевидная структура капилляра при прочих равных условиях позволяет перемещать больший объём воды в меньшем пространственном объёме по сравнению с прямолинейным и криволинейным капиллярами той же длины.