Математическое моделирование при расчетах на живучесть деформированного твердого тела

Введение. Основной задачей расчета и проектирования элементов строительных конструкций является выбор материала, размеров и условий опирания, обеспечивающих прочность конструкций при заданном нагружении. Так, например, в процессе э ксплу атации могут возникнуть ситуации, в которых принятые и 118

реализованные механические, геометрические и структурные параметры конструкции внезапно изменяются по причинам, не предусмотренным проектом. Задачи, позволяющие рассчитать статическую и динамическую прочность, устойчивость являются основой в проектировании конструкций. [1]. Процесс вычислений в значительной мере можно упростить с использованием таких прикладных пакетов как Mathcad, Maple, Matlab, Mathematica и др. Их отличие, например от Excel, заключается в том, что они позволяют получить результат в аналитическом виде. Так, например, программа Mathcad дает возможность не только проводить технические расчеты, но и снабжена графическим интерфейсом, позволяющим наглядно увидеть результат. Все это становится возможным из=за использования достаточно большого количества встроенных математических функций, при этом математическое выражение достаточно наглядно и понятно.

В связи с возрастающими и усложняющимися требованиями к долговечности, прочности, устойчивости и надежности строительных конструкций зданий и сооружений интенсивно совершенствуются методы расчета и проектирования инженерных конструкций. На напряженно-деформированное состояние конструкции существенно влияет ее неоднородность как естественная, так и технологическая, которая проявляется в процессе изготовления и эксплуатации отдельных элементов или строительных конструкций в целом. Широта класса неоднородных тел определяет большое практическое значение. [1, 2, 4]

Конструирование, оптимальное проектирование вызывают необходимость аналитических решений проблем прочности и устойчивости различных конструкций. Проблема математического моделирования сводится к решению дифференциальных уравнений в частных производных четвертого или второго порядков с переменными коэффициентами. Получение точных решений для таких дифференциальных уравнений возможно лишь в конечном числе случаев и сопряжено с определенными трудностями.

В настоящей работе предлагается математический метод решения задач для неоднородных стержней в статике и динамике, а также построение математической модели динамики и напряженно-деформированного состояния элементов конструкций, которые подвергаются внезапным выключениям связей и изменениям структуры.

При внезапном изменении расчетной модели конструкции, будь то изменение условий опирания или продольное разделение конструкции на несколько частей, неизбежно возникновение динамического процесса, который выражается в возникших колебаниях. Снятие опорных реакций предполагается равносильным внезапному приложению сил противоположных по знаку реакциям, а снятие внутренних сил — внезапному приложению сил противоположных по знаку внутренним силам, возникающим в связях. [1, 3, 4]

Алгоритм метода представлен на примере уравнения четвертого порядка с переменными коэффициентами, описывающего свободные поперечные упругие колебания стержня с произвольными законами распределения модуля упругости и осевого момента инерции

поперечного сечения вдоль оси стержня

Г

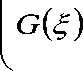
8 2 V )

85 2 J

+

8 2V _ s (5)---2 = q 0(1)

„ Z - V гДе ^ = ^Z ’ V = 1 ’

z

t EJ l2 4Pf ’

EJ       pf       ql3

-----, s =----, q o = —, E 0 J 0      P 0 f 0 ⁰ EJ

z — осевая координата ( 0 < z <  l ); l — длина стержня; t — время; V = V ( Z , t ) — прогиб; f — площадь поперечного сечения; J — момент инерции; p — плотность материала; E — модуль упругости

материала; E 0 , J 0 , Р 0 , f 0 — некоторые значения механических

и геометрических характеристик стержня. [4, 10]

Предполагается нагружение стержня

равномерно

распределенной нагрузкой заданной интенсивности q .

Специальным образом составляются уравнения

[ G (sV^^fi ] + (s (5)+gi^Sl)8^852 (     852)               8т2

= q 0 (2),

которые   отличаются от исходного (1) наличием

дополнительных функций во втором коэффициенте, однако структура

его близка к структуре исходного уравнения. Для уравнений (2)

находят достаточно точные решения

fi = fi(s)

( i=1,2,3,4 ), которые

принимают в качестве приближенного решения уравнения (1). Такой подход представляется рациональным, несмотря на то, что точное решение не просматривается. В этом случае строятся точные решения определенным образом измененной (2) первоначальной (1) задачи. Подобное изменение достаточно точно, зависти от степени приближения. [4, 5] Используя степенные ряды для приближенного вычисления значений выражения можно достаточно точно получить требуемый результат. Решение дифференциальных уравнений ищем в виде разложения в ряд Тейлора с использованием производных.

Возможно также использование интеграла Дюамеля, замена рядов оценкой остаточных членов при слабой

пределами конечных сумм с неоднородности функции gi = gi (£).

Для нахождения

оптимального решения возможно использование функции связывающей координаты и время для определения напряжения и деформации. Такой подход позволяет решать оптимизационные задачи по выбору закона распределения площадей поперечных сечений, обеспечивающего при заданном объеме материала минимальное напряжение в опасном сечении при внезапном снижении степеней статической неопределимости. [1, 4]

Кроме того, изложенный подход может быть использован при анализе напряженно-деформированного состояния балки внезапно расслаивающейся на произвольное количество слоев одинаковой толщины и позволяет решать задачи о структурных изменениях для составных по Ржаницыну стержней и пластин. Следует отметить, что сила, приложенная к нему в результате изменения переходит на другой материал. [6, 7, 9]

Результаты исследований перечисленных выше задач показали, что внезапное изменение расчетной схемы существенно влияет на напряженно-деформированное состояние элементов конструкции.

• 1.    При выборе формы поперечного сечения расчет статических напряжений является недостаточным.

• 2.    Количество изменяющихся связей напрямую связано с динамическим и статическим напряжением.

• 3.    Чем жестче закреплен стержень, тем больше будет скачек напряжений в случае исчезновения хотя бы одной связи.

• 4.    При прогрессирующем разрушении, именно в начале процесса происходит резкое увеличение напряжений.

• 5.    Чем больше число слоев, на которые расслаивается балка, тем большие динамические напряжения и деформации она испытывает.

Выводы. Предложенный алгоритм позволяет получать решения не только для дифференциальных уравнений четвертого порядка, описывающих поперечные колебания стержневых систем, но и решать уравнения второго порядка. Так, например, в армированном стержне произвольного сечения, подверженном растяжению, в котором возможен внезапный обрыв арматуры или разрушение матрицы, возникают кратковременные продольные колебания. В случае еще не разрушенного стержня, часть растягивающей силы приходится как на арматуру, так и на матрицу. Решение задачи на примере неоднородных стержней в статике и динамике возможно с построением математической модели динамики и напряженно-деформированного состояния элементов конструкций, которые подвергаются внезапным выключениям связей и изменениям структуры.