Математическое моделирование процесса десублимации изотопов водорода в лазерной мишени

Настоящая работа посвящена решению одной из задач математического моделирования технологических процессов производства лазерных мишеней. Это направление исследований в общей проблеме управляемого термоядерного синтеза занимает в настоящее время одно из главных мест. Сам управляемый термоядерный синтез с инерциальным удержанием, или ИТС — инерциальный термоядерный синтез, основан на очень быстром доведении ядерного топлива до сверхплотного состояния, а с этим и до термоядерных температур [1–4]. Контейнер, содержащий ядерное топливо, а как правило, это дейтерий-тритие-вая смесь, называется мишенью. Исследования показывают, что абляционное сжатие сферически или цилиндрически симметричной топливной мишени для формирования центра горения является энергетически оптимальным процессом. Для этого мишень симметрично облучают со всех сторон лазерным излучением или иными видами излучения (рентгеновское, ионные и электронные пучки) [5–6]. При этом энергия излучения поглощается во внеш- ней абляционной оболочке мишени, абля-тор испаряется, ионизируется и разлетается со скоростью порядка 100 км/с. Создаваемый при таком разлете реактивный импульс давления сжимает неиспарившее-ся топливо, которое в центре мишени достигает необходимой плотности и температуры. Последнее и позволяет зажечь D-T термоядерную реакцию. образующиеся в результате реакции альфа-частицы с энергией 3,52 МэВ теряют её во внутреннем слое холодного топлива и нагревают его. Образуется фронт термоядерного горения, который быстро распространяется в слое холодного топлива. Теоретические расчёты показывают, что для достижения условия брейкивен (breakeven — условие, при котором энергия выхода в реакции термоядерного синтеза не меньше вложенной) необходимо существенное сжатие и нагрев вещества мишени до температур 10 кэВ. Для этого можно использовать одну из трёх схем облучения топливной мишени. Это прямое облучение, прямое зажигание, или быстрый поджиг, и непрямое рентгеновское облучение. Структура мишени и её физические характеристики, вообще говоря, зависят от схемы облучения, но неизменной остаётся одна черта:

мишень должна представлять собой сферическую оболочку с твёрдым слоем D-T топлива внутри нее. На первый взгляд, это простая конструкция. Но она оказалась достаточно сложной при её технической реализации [7–8]. Первая проблема состоит в том, чтобы доставить топливо внутрь многослойной полистироловой оболочки мишени, не разрушив ее. Одно из решений — поместить оболочку в камеру с D-T газообразной смесью, находящейся под давлением. В результате газ проникает через стенку мишени, постепенно заполняя ее. Давление газа внутри мишени повышается, а вместе с этим следует повышать и внешнее давление, но так, чтобы не разрушить оболочку. Поскольку в оптимальном по быстродействию режиме разность внешнего и внутреннего давлений не должна превышать критического значения, при котором может разрушиться оболочка, необходимо с высокой степенью точности определять давление газа внутри мишени, измерить которое невозможно. При этом внутреннее давление может достигать от 300 до 1000 атм. Было необходимо разработать адекватную математическую модель заполнения газопроницаемых оболочек до высоких давлений [9–10], когда состояние газа описывается уравнением Ван-дер-Ваальса. Результаты модельных расчётов в дальнейшем использовались при конструировании системы заполнения оболочек в лаборатории термоядерных мишеней нейтронно-физического отдела ФИАН им. П.Н. Лебедева. После заполнения газом мишень помещается в криостат, где охлаждается до температур фазовых переходов, в результате которых газ оседает на внутренней стенке мишени в виде твёрдого слоя. В работе изучается процесс вымораживания газообразных изотопов водорода на внутренней стенке оболочки лазерной мишени без образования жидкой фазы, то есть процесс десублимации.

• II.    Предположения модели и некоторые вспомогательные соотношения

На рис. 1 изображена лазерная мишень, которая представляет собой многослойную полистироловую сферическую оболочку, внутри которой находится дей-терий-тритиевая газообразная смесь, охлаждённая до температуры тройной точки. В процессе десублимации на внутренней стенке оболочки вымерзает твёрдый шарообразный слой изотопов водорода, который далее будем называть криогенным, или топливным слоем.

оболочка

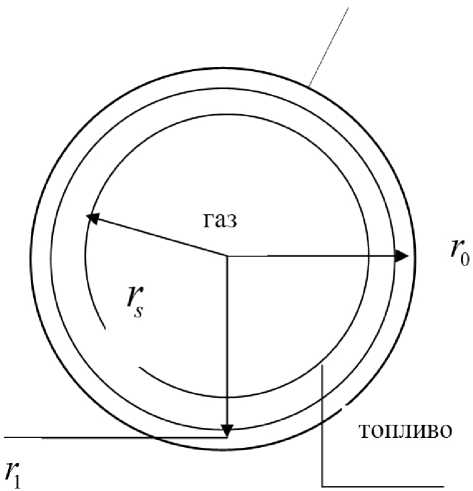
Рис. 1

Будем считать, что в процессе десублимации газ внутри оболочки представляет собой насыщенный пар, и его температура, давление и плотность связаны уравнением Клапейрона–Клаузиуса. Такой подход представляется более реалистичным, чем предположение о постоянстве температуры газообразной фазы, сделанное в работе [11]. Поэтому полученные ниже результаты несколько отличаются от тех, что были приведены в статье [11].

Вначале проведём анализ уравнения Клапейрона–Клаузиуса для газа, термодинамическое состояние которого описывается уравнением Клапейрона–Менделеева. Последнее допущение является в некоторой степени идеализацией и оправдывается в первую очередь попыткой аналитического решения поставленной ниже задачи.

Давление p, температура T и удельные объёмы vg ,vs газообразного и твёрдого водорода в области тройной точки на фазовой диаграмме связаны уравнением Клапейрона–Клаузиуса dp λs dT = T (Vg - Vs) ’ где λs — удельная теплота сублимации. Для водорода и его изотопов в окрестности тройной точки отношение vs/vg мало, поэтому предыдущее уравнение можно приблизить уравнением dp    λs dT = Tvg'

Термодинамическое равновесное состояние газообразной фазы внутри оболочки описывается уравнением Ван-дер-Ваальса. Наше упрощение сводится к предположению об идеальности газа, то есть к уравнению Клапейрона-Менделеева pV = = m RT, откуда следует, что Vg = m = RT, (μ — молярная масса газа). Подставим это выражение в (1) и проинтегрируем уравнение (1) по T . Получим хорошо известное соотношение между давлением и температурой идеального насыщенного пара:

p = C exp | -RTy       ⁽²⁾

Наша ближайшая задача найти связь между толщиной криогенного слоя w = r 1 — - r s и температурой газа внутри оболочки, которая предполагается однородной по объёму. Обозначим T _tp ,ρ ₀ — температуру, при которой начался процесс десублимации, и начальную плотность газа в мишени. Пусть r 1 ,r s — внутренний радиус оболочки мишени и расстояние от центра мишени до внутренней поверхности шарового криогенного слоя соответственно. Тогда толщина криогенного слоя w = r 1 — r _s , а его объём V _s = V 0 — 3 nr ^ = 3 п ( r 3 — r 3 ) , где V 0 — начальный объём газа. Левую часть уравнения (2) согласно закону Клапейрона-Менделеева запишем как

P_RT = P 0 V 0 — P s V s RT μ        V 0 - V _s    μ

) ,        (3)

= p 0 RT ( _{— —} ¹ — V ЕЦ (1 — w ) ³

где v = pO ^ 0,22 для изотопов водорода при температуре, близкой к тройной точке, а w = w — безразмерная относительная толщина криослоя. Подставляя выражение (3) в левую часть формулы (2) и учитывая, что при T = Ttp плотность газа р = ро и относительная толщина криослоя w = 0, получим значение постоянной

ρ 0 RT tp

C =----- exp ^μ

T^α tp   ^.

Здесь а = ^ т Т ~ ⁹⁹⁰² К ~ 243 К. Вновь

R       8 , 13

подставим (3) в левую часть (2) и исполь- зуем только что полученное выражение для C. Теперь (2) примет вид

1 —        = VT P exp { а ( Т-* — T ^- 1 )} =

(1 — w ) T

= vG ( T ) .

Разрешим это уравнение относительно w. Получим w = 1 —

1 / 3

1 —V

1 — VG

Если v = p 0 мало, то (4) можно разложить в ряд по малому параметру ν и получить аналитическую зависимость w ( T ) :

w w = — = r1

= 3[1 — TT exp { а ( T-¹ — T - 1 )} + O ( V 2 ) . _а ⁽⁵⁾ Нетрудно видеть, что dT Tie т)    =

= eт (1 — т) С 0, если T ^ а ~ 243K, что справедливо для того диапазона температур, при котором происходит десублимация. Отсюда следует, что правая часть (4) или (5) является монотонно убывающей функцией T . Таким образом, при убывании T от Tо до 0 величина w (T) монотонно возрастает от 0 до примерно wmax = 1 — — 33/1 — v ^ 0,08. Если V = р0 мало, то wmax ≈ 3ρρ0 . Из уравнения (4) (а при малых значениях ν из (5)) получаем транс- цендентную зависимость

T = F ( w ) ^ Fpw),

где F ( w ) — функция, обратная к функции, стоящей в правой части соотношения (4) (или (5)).

• III.    Математическая постановка начально-краевой задачи

Ниже T i ( r,t ) , k i ( T ) , C i ( T ) , p i ( T ) обозначают температуру, коэффициент теплопроводности, теплоёмкость и плотность веществ соответственно. Индекс i = sh ,s,g , где sh относится к оболочке, s,g определяют криогенный слой и газ. Тепловые потоки в оболочке и криослое описываются в сферически симметричном случае уравнением теплопроводности

P i C i ГТ = Хд-^{Г 2} k i IT,i = sh ,s.    (7)

dt    r ² dr dr

Коэффициент χ определяет отношение характерного пятна контакта, через которое идёт теплообмен с внешней средой, к поверхности мишени. Если мишень полностью погружена в охлаждающую среду, то для тонких оболочек x ~ 1

На внешней поверхности оболочки справедливо равенство

T sh ( r 0 ,t ) = T ext ,             (8)

где T ext — внешняя температура, которая может зависеть от времени. Условие

T sh ( r I ,t ) = T s ( r I ,t )            (9)

определяет непрерывность температуры на границе оболочка–криогенный слой. Баланс тепловых потоков на этой границе задаётся равенством

∂Tsh         ∂Ts ksh dr |r=ri    ks dr |r=ri

Баланс тепловых потоков на границе криослой–газ учитывает тепло, выделяющееся при десублимации,

∂T s

^Xk ^s dr ' r = r i ⁽ t )

ТРУДЫ МФТИ. — 2009. — Том 1, № 4 слагаемое справа равно нулю и последнее равенство запишется в виде

∂T _s                 dw

^Xk ^s" dr ' r = r i ^{— w (} t ) = ^{— X s P s}dtt'

Равенство температур на границе газ-криогенный слой имеет вид T _s ( r 1 — — w ( t ) ,t ) = T g ( t ) , которое согласно (6) записывается как

T s ( r 1 — w ( t ) ,t ) = F ( w ( t )) . (12)

Считаем, что процесс десублимации начинается в момент t = 0 . Тогда начальные условия таковы:

w (0) = 0,(13)

Tg (0)= Ttp,(14)

T.h(r,0 = T(r).

где T tp — температура, при которой начался процесс десублимации, например, температура тройной точки газа, а т ( r ) — распределение температур внутри оболочки в начальный момент времени. Считаем, что граничные условия для т ( r ) согласованы с граничными условиями нашей задачи, то есть

T ( r о ) = T ext , т ( r 1 ) = T s ( r 1 , 0) = T g (0) .

Сразу отметим, что решение поставленной выше задачи «забывает» начальные условия, поэтому условие (15) далее существенной роли играть не будет.

Введём безразмерную температуру 9 = = тГ. Для физических коэффициентов криогенного слоя ks,cs,ρs используем линейные аппроксимации ks = 5 • 10—3

Дж см · с · К

C s = C s • 9 , где C s = 1 Дж , p s = 0 , 09 сМг з .

Для упрощения исследования поставленной начально-краевой задачи (8)–(15) для системы уравнений (7) запишем её в безразмерной форме. Для этого введём следующие переменные и параметры.

Характерное время процесса десублимации можно оценить величиной

= Xk g

∂T g ∂r

r = r 1 — w ( t )

-

dw λ s ρ s dt .

∗ t 1

Здесь λ _s — удельная теплота десублимации. Поскольку температура газа предполагается однородной по объёму, то первое

P 0 V g X s

Xk sh ^{4 nr} о ² ( T ^-— T ^ )

Здесь X _s ~ 990 Дж / г — удельная теплота сублимации.

Введём т = t — безразмерное время;

t ₁

• 9 i = TjTi- — безразмерная температура в слое i = sh ,s,g ; x = r 0 r , u = ^r 1 ^{— r}- — без- r 0 - r 1          w max

размерные пространственные переменные в оболочке и криослое соответственно; 5 = = r 0 -o r ¹ — безразмерная толщина оболочки; параметр δ ^{- 1} называется ещё аспектным отношением. Пусть далее w = ww-- безразмерная толщина криогенного слоя.

Переменная x будет использоваться для точек оболочки. Очевидно, что на её внутренней и внешней границах значения x равны 1 и 0 соответственно. Пространственную переменную u будем использовать для точек криогенного слоя. На внешней и внутренней границе этого слоя u равно соответственно 0 и w .

Будем считать оболочку стеклянной (стекло «пирекс»). Зависимость c _g , c _sh , k _sh от температуры можно приближённо задать линейными соотношениями k _sh = = k sh • (1 + a sh 9 ) , c sh = c sh • (1 + e sh 9 ) , где 9 = Т /T ext — безразмерная температура.

В частности, параметры, входящие в приведённые выше формулы для водорода, заключённого в стеклянную оболочку под давлением 250 атм, при температурах порядка 300 К имеют следующие значения:

Вт ksh = 1,4 • 10-3 см-К ,ash = 0,14,

C sh = 6 • 10 ² -Дж ,e sh = 0 , 2 , P sh = 2 , 3 г / см ³ . г • К

Теплоёмкость c g для газа практически не зависит от температуры и равна c _g = = 1 , 5 R = 6 , 2 ДЖ . Плотность газообразного водорода при давлении 250 атм в оболочке радиуса r 0 = 0 , 5 мм при комнатной температуре равна р о = p g = 2 • 10 ^{- 2} сМг з .

В безразмерных переменных система уравнений (7) для 9sh (х,т) ,9s (u,т) примет вид d9sh _    1

г ⁽¹+ М»к )- ^ 7 = (1 _ 5х ) 2 ^х

Величины

( 5r o ) 2 p sh C sh χk sh t ^∗ ₁

^{3 5p} sh ^c sh • ⁽ T tp ^_ T ext )

λ s ρ 0

0 , 005 , δ ₁ ² r ₁ ² ρ s c s χk s t ^∗ ₁

= 3( T_tp _ T_ex) ^{P s C s ( 5 1 (1    5 )) 2} k sh « 0 , 0005

tp ext        ρ0 λsδks            , и y = ~ ~ 10.

ε 1

Параметр ε является малым. Таким образом, система (16)–(17) является сингулярно возмущённой системой полулинейных параболических уравнений. Краевые условия (8)–(9) примут вид

9sh(0 ,т) = 1,(18)

9sh (1 ,т) = 9s (0 ,т).(19)

Балансовое соотношение (10) запишется как d9s (0,т) = 51riksh(1 + ash9sh(1 ,т)) d9sh (1 ,т)

∂u               δr0ks

=(20)

wmax dw   χks Text ∂θs sPs “t^ dk = 51 ri дй 1 u=w(T) , или dw _ ^d9s (u,r) । dT = ^ du   1 u=w(T)

где

. =       5r 2 k s p 0 T ext

3 52r 2 k_shp_s ( T tp   ^Tex:t

Равенство безразмерных температур газа и криослоя на границе их раздела согласно (6) имеет вид 9s(w(т),т) = f (w(т)), где z=x _ F (51 w) f w = —---.

T ext

Начальные условия (13)–(15) тоже очевидным образом записываются в новых обозначениях:

w (0) = 0 ,9 g (0) = ^ t^ , T ext

9 sh ( x, 0) = ^ ( x ) ,x E [0 , 1] .       (21)

Поскольку начальные условия согласованы с краевыми, то pi (0) = 1 ,^ (1) = 9 _g (0) .

В дальнейшем при решении сингулярно возмущённой задачи (16)–(21) мы ограничимся построением лишь регулярной части решения, которая «не помнит» начальные условия. Погранслойная (или сингулярная) компонента решения быстро их «забывает».

Плотность газа и безразмерная толщина криогенного слоя W = w/r 1 при предположении об отсутствии жидкой фазы в каждый момент времени связаны соотношением рд(т) = ps f1 - f1 - -) (т^м )1 , Ps) V1 — w (т)

(22) где ро = pg(0). Как отмечалось ранее, процесс десублимации закончится, если в некоторый момент плотность газа станет достаточно малой, в идеале равной нулю. В этом случае выражение в квадратных скобках обнуляется, и мы имеем 1 — w = = 3/1 — v, где v = р0. Отсюда следует, что максимальная безразмерная толщина wmax криослоя равна приблизительно wmax = 1 — V71 — V, а Wmax = Г1Wmax. Таким образом, максимально возможное значение безразмерного времени процесса десублимации τmax получаем, решая уравне- ние w (тmax) — wmax, или в других обозначениях:

W ( T max ) = 1 .

Если же процесс десублимации заканчива- ется тогда, когда давление паров водородных изотопов больше нуля и равно

ρg∗ , то в этом случае согласно (22) вели- чина

W * = 1 —

ρ s ρ s

— р _о

—

ρ

∗ ^g

и продолжительность процесса десублимации τ ^∗ в безразмерных единицах есть корень уравнения

W ( т * ) = W* ——.

w max

Таким образом, основным результатом решения задачи (16)–(21) для нас будет построение функции W ( т ) , описывающей динамику изменения толщины безразмерного слоя.

Решение поставленной задачи будем искать в виде суммы регулярных и сингулярных слагаемых:

0 sh ( х,т,Е ) = 0⁽ ( r^ х,т,Е ) + n ^(sh) ( х,т,Е ) ,

0 s ( х,т,Е ) = 9 s^r ) ( х,т,Е ) + П ^{( s} ) ( x,t,e ) .

Здесь т = т/e . Ограничимся поиском нулевого приближения регулярной составляющей решения, которое ищем в виде асимптотического ряда по степеням ε

∞

⁰ ( r ) ⁽ х,т^,Е ) = ^{0 (О) (} х,т ) + ^ ^E k ⁰ i k ^{) (} х,т ) , k =1

i = sh ,s.               (23)

Сингулярная составляющая ищется так, как описано в Приложении. Можно показать, что эта составляющая быстро стремится к нулю, и ею можно пренебречь.

• IV.    Построение приближённого решения задачи о десублимации

В данном параграфе будет построено нулевое приближение задачи (16)–(21), то есть будут найдены первые члены 0 ^(О) ( х,т ) , i = sh ,s рядов (23). Запишем уравнение (16) в виде

Ed0sh = H (0sh ,x),(24)

∂τ где нелинейный оператор

H ( 0 sh ,x ) =

_1

= (1 — 5x)2(1+ esh0sh) X x d (1 — 5x )2(1 + ash0sh) d0sh.

∂x∂x

Для того чтобы найти нулевые приближения уравнения (24), положим (см. Приложение):

H ( 0 ^н ,x ) = 0 , или

— ^{(1 —} 5x ^{) 2} (1 + ^a sh ^{0 ( h )}) -x^ = ⁰ . ⁽²⁵⁾

Аналогично в уравнении (17) нулевое приближение удовлетворяет уравнению d (1 — 51 u )2 d-^ = 0.      (26)

∂u         ∂u

Краевые условия для θ _s ⁽⁰ _h ⁾ ,θ s ⁽⁰⁾ имеют вид (18)–(21), где вместо символа θ следует использовать θ ⁽⁰⁾ .

Интегрируя (25)–(26) по x и u соответственно, получим

Определим вид c o ( т ) . Подставим (30) в (28) и воспользуемся соотношением (37). Тогда выражение для

^{e (o) (} uT ^{) _}

(1+ ^a sh 6' (i! ^{( x}T )) _ c _o ( T )

ah        ~ 6 (i - 6x )^{+ c 1 ( T )} ’

*14 ^U,T ) = TTT^ + d 1 ( t ) ■   (28)

6 ₁ (1 - 6 ₁ u )

α sh

L /      + (1+ a sh ) ² — 11

1 —6

ηc 0 u

1 — 6 1 u

Используем его в (21). Тогда для переменной z _ a _sh c o получим иррациональное уравнение

Из (27), используя (18), найдём c 1 ( т ) и, подставив вновь в (27), получим

C o ( T ) x _

1 — 6x

2 г

-z r + (1 + a sh ) ² — 1 —6

_ a s_h f (w) —

^_ 5--- [ ^{(1 +} “ sh ^ ^{(0) ( X,T )) 2 — (1} + ^a sh ^{) 2}] ■

2a _sh L                                      J

Из (28), (29) и условия (19) равенства температур на границе оболочка — криослой следует выражение для d 1 _    [j ^hcT + (1+^sh)2 — 1]

^a sh     ^{1 — 6}

Дифференцируя (27) по x, а (28) по разим д§)_ _       c o( T)_______ dx (1 + ash0^(1 — 6x)2 ’ des0 _   do(t)

du (1 — 6 1 u ) ²

ηwz

1 — 6 1 w,

которое равносильно квадратному уравнению

a 0 z 2 ^{— 2} [1 ⁺ a o ^{(1 + a} sh ^{f )]} z ⁺

^{+ a} sh ⁽ f ^{— 1) [2 + a} sh ⁽ f ^{+ 1)] _ 0}

d 0 ^- δ 1 ^.

u , вы-

Подставим правые части (31) в (20) и найдём связь между d ₀ и c ₀ d ₀ ( т ) _ nc 0 ( т ) ,

δ1r1ksh где П _ 6roks(1 — 6)2 ■

Используем в (20) выражение (31). С учётом (37) дифференциальное уравнение (20) примет вид

dw _ .    c o ( t )

dT     ¹ (1 — 6 1 w ) ’

где £ 1 _

r 0 ρ 0 T ext

^{3 6} 1 r 1 P s ⁽ T tp ^— T ext ⁾

в предположении, что 1 — 6 ~ 1 . Здесь

ηw ao   1 — 6 1 W

Поскольку n ~ 0,47,6 1 _ Wmax ~ 0,08, то для значений w E (0,0,1) согласно (32) полученное квадратное уравнение можно заменить линейным, положив ao _ 0. Если w E [0,1,1], то требуется решать квадратное уравнение, взяв в качестве решения меньший из корней, поскольку он при ao ^ 0 стремится к решению аппроксимирующего линейного уравнения. Таким образом, мы получим co _ Ф wu (т)), где

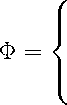
( f ( w ) - 1 )[ ^{2+ a} sh ( f ( ^w ) ⁺¹ )] 2 [ 1+ a o ( w )( 1+ a sh f ( w ))] 1+ a o ( w )( 1+ a sh f ( w )) -V D a sh a 0 ( w )

w E [0 , 0 , 1);

,w E [0 , 1 , 1] ■

В этом выражении

D ( w ) _

^{_ 1} +² a o ⁽ w ^{)(1 + a} sh ^{f (} w ^{)) +} a o ⁽ w ^{)(1 + a} sh ^{) 2} .

Подставим (40) в дифференциальное уравнение (38), проинтегрируем последнее и

получим связь между безразмерной тол щиной w = w и безразмерным временем wmax процесса десублимации т = t:

t

Аналогично пусть θ есть корень уравнения

W ( 0 ) = 0 , 1 .

т =

w

1 [ ⁽¹ - ⁵ 1 s ) _d8

€ J  Ф( S )

Тогда функция Ф ( w ) следующим образом зависит от температуры θ :

Максимальное время течения процесса десублимации равно

Ф( 0 ) =

^т max

£ Г (1 - ⁵ 1 s )

€ J Ф( s )

⁽ О — 1)[2+ g _sh ⁽ 6 + ¹ )] 0 g 1+ A ( 6 )(1+ a _s h 9 ) - VW )

a sh A ² ( 6 )

[ 0,0 tp ]          ;

,0 G [ 0 min ,0 ] .

Здесь

В интеграле (33) используется функция Ф (w), для определения которой требуется знать функцию f w . Последняя задаётся неявно, что при вычислениях может создать неудобства. Во избежание этого запишем (33) другим способом, используя вместо w переменную θ. Из равенства (4) следует w = W (0), (34)

a ( 0 ) =

nW ( 0 )

1 - 5 1 W ( 0 ) ^,

D ^{( 0} ) = ^{1 + 2} A ^{( 0 )(1}+ ^a sh ⁰ )+ A ^{2 ( 0 )(1} + ^a sh ^{) 2} .

Из сказанного выше и (33) следует, что

где

W ( 0 ) =

w max

11 (1

1 -v

- vG ( 0 )

Функция

И -

θtp т <6)=^ i ^-10? B <6) G' (0 > d0.

θ

θ

G ^{( 0} ) = -0 - exp⁽ а ^{( 0 - - 0 1} )) .

Здесь а = т^ = R^ _t ~ 60 для водорода.

Очевидно,

G ( 0 ) = -^ exp( а ( 0 -p¹ - 0 ^{- 1} ))( аг ¹ - 1) .

Из (34)–(35) получаем выражение для

^ = -в (0) d (0), dθ где

Максимальное значение длительности процесса десублимации равно т ( 0 _min ) . Связь между безразмерной толщиной криогенного слоя и безразмерной температурой задается соотношениями (34)–(35).

Ниже на рис. 2 и 3 приведены графики функций w ( т ) ,w ( t ) для мишени, параметры которой: мишень — сферическая оболочка из стекла «пирекс» радиуса 0 , 5 мм, толщины 0 , 025 мм. Начальное давление газообразного водорода в оболочке 250 атм. Здесь можно считать, что расчётное время отражает реальность, если в мишени сохраняется более 10% начальной массы газа.

3 w max (1 - vG ( 0 )) ^{4 / 3} .

Пусть 0 _min — безразмерная температура, при которой заканчивается процесс десублимации, то есть

зависимость безразмерной толщины криогенного слоя от безрамерного времени

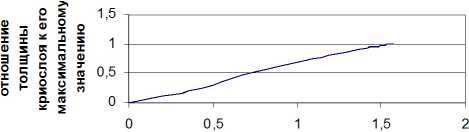
безразмерное время

Рис. 2

W ( 0 min ) = 1 .

зависимость толщины криослоя от времени

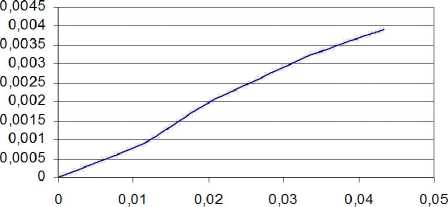
время в с

Рис. 3

• V.    Приложение

Рассмотрим дифференциальное уравнение в банаховом пространстве B

Az = ^{H ( z,t} )

с начальным условием z (0) = п.

Здесь е — малый параметр, а H ( z,t ) — нелинейный, вообще говоря, неограниченный оператор B х R ^ B , бесконечно дифференцируемый по t , допускающий существование бесконечно дифференцируемого решения z о ( t ) уравнения

H ( z,t ) = 0 .              (38)

Изложенная ниже схема решения уравнения (36) принадлежит профессору А.М. Тер-Крикорову [12]. Она является модификацией подходов, изложенных в [13].

Обозначим H k ( и 1 ,и 2 ...,и _к ,t ) полилинейные операторы степени к = 2 , 3 , ... с областью определения D С B и значениями в B . То есть

Hk (аи 1 ,аи 2 ...,auk ,t) = ak Hk (и i ,и 2 ...,Uk ,t), и для любого i

H k ( и i , ..., U i + V i , ..., U k ,t ) =

Пусть далее для некоторого 5 >  0 и всех и таких, что |и| С 5 :

∞

H ( z ₀ ( t )+ u,t ) = L ( t ) и + 52 H _k ( и,и, ..., и,Ь ) .

k =2

Здесь L ( t ) = H z ( z о ( t ) ,t ) — линейный оператор, являющийся производной Фреше оператора H ( z,t ) по z в точке z ₀ ( t ) .

Решение уравнения (36) будем искать в д z (t,E ) = Z (t,E ) + П(t,e ),(40)

T = t, п(0,е) = п - Z(0,е).

Подставим сумму (40) в уравнение (36). Получим

EdZ^t^ + dП(т,е ) = H ( Z () ,t) + dtdτ

+ H [ Z ( ET,E ) + П( T,E ) ,ET )] — H ( Z ( ET,E ) ,ET ) .

Положим

\    = H(Z(t,E) *),(42)

d П( t,e ) dτ

= H [ Z ( ET,E ) + П( T,E ) ,ET ] — H ( Z ( ET,E ) ,ET ) (43) с начальным условием (41). Если уравнения (41)–(43) выполняются, то сумма (40) является решением задачи Коши (36)–(37).

Решение системы дифференциальных уравнений (42)–(43) будем искать в виде формальных рядов по целым степеням параметра ε :

Z ( t,E ) = z 0 ( t ) + £ z k ( t ) E k ,    (44)

k =1

П( T,E ) = ^2П k ( T ) E ^k , П о (0) = п — z о (0) .

k =0

(45) Подставим ряды (45) в правую часть уравнения (42). Получим согласно (39):

H ( z o ( t ) + ²² z k ( t ) E k ,t ) = k =1

= ² ( L ( t ) z k ( t )+ g k ( z o ( t ) , ..., z k - 1 ( t ) ,t )) E ^k .

k =1

(46) Выражения для операторов gk определяются согласно (39) операторами L, H2, ..., Hk. Например, g 1 = 0, g2 = = H2( z 1 ,z 1), g 3 = H2( z 1 ,z 2) + H2( z 2 ,z 1) + Hз( z 1 ,z 1 ,z 1).

Подставляя (44), (46) в (43) и приравнивая коэффициенты при одинаковых степенях параметра ε, получим рекуррентную систему уравнений dzk-1 = L(t)z-(t) + g-(zo(t), ..., Zk-1(t),t), k > 1.                 (48)

Предположение 1. Линейный оператор L ( t ) = H z ( z o ( t ) ,t ) обратим в D .

В этом случае уравнения (48) последовательно разрешимы и

Z k ( t) =

= L ^{- 1 (} t ) W - g k ^{( z} o ⁽ t ) ,..., k - i i ⁽ t ) ,t )] .

(49) Подставим ряды (44)–(45) в уравнение (43). Приравняем слагаемые при нулевых степенях параметра ε и положим в коэффициентах ет = 0. Получим d По( т) = dτ

= H [ z о (0) + П о ( т ) , 0] - H ( z о (0) , 0) . (50) В силу уравнения (3) второе слагаемое в правой части равно нулю. Из последнего уравнения и представления (4) с учётом сделанного замечания получаем задачу Коши для П _о ( т ) :

d П            ^

—— = L (О )По(т) + ^^ Hm (По, ..., По,0), dτ m=2

П о (0) = п — z о (0) .         (51)

Пусть нелинейный оператор H ( z,t ) представим в окрестности точки z _о (0) + П _о ( т ) в виде

H ^{( z} о ⁽⁰⁾+^П о ^{( т ) + и,Ет} ) = H ⁽ z о ⁽⁰⁾+^П о ^{( т} ) , ⁰⁾ +

∞

+Л( т ) u + 52 h - ( u,u, ..., и,т ) ,     (52)

k =2

где h-(ui,u2...,u-,т) —полилинейные опера торы от u 1, ..., uk, то есть hk (au 1 ,au 2 ...,auk ,т) = a- hk (u 1 ,u 2 ...,uk ,т), hk(ui,..., ui+vi,..., u-т) = hk(ui,u2...,u-,т)+ +hk(ui, ..., Vi, ...u-,т), а Л(т) — линейный оператор, являющийся производной Фреше оператора H(z,Eт) в точке z = zо (0) + По(т).

Подставим ряды (44)–(45) в правую часть уравнения (43). Получим согласно (39), (52):

H [z о ( ет ) + П о ( т ) + ^ ( z - ( ет ) + П - ( т )) Е^к ,Е^

-

-

H f z о ( Ет ) + ^ z- ( Ет ) Е ^- ,Е ^ =

= H ^{[ z} о ⁽⁰⁾ + ^П о ^{( т} ) , ^{0] —} H ^{( z} о ⁽⁰⁾ , ⁰⁾ +

+ H [z о ( Ет ) + П о ( т ) + ^ ( z - ( Ет ) + П k ( т )) е ^- ,е^ —

— H [ z о ( Ет ) + П о ( т ) ,Ет ] +

+ ^{H [ z} о ^{( Ет} ) + ^П о ^{( т} ) ^{,Ет ] — H [ z} о ⁽⁰⁾ + ^П о ^{( т} ) , ^0] +

+ H ( z о (0) , 0) —H f z о ( Ет ) + ^ z - ( Ет ) Е ^- ,Е ^ =

= ^{H [ z} о ⁽⁰⁾ + ^П о ^{( т} ) , ^{0] — H ( z} о ⁽⁰⁾ , ⁰⁾ +

∞∞

+Л( т ) ^ z s ( Ет ) E s + Л( т ) ^ П - ( т ) Е ^- + s =i                    k =i

∞∞

+ 52 hm (Z, ..., Z,ET) — Л(т) 52 zs (Ет) Es — m=2                        s=i

∞ k

— ЕЕ Е h m ( z i 1 ,...,z i m ,Ет ) Е ^- +

∞

+ 52 Q - ( z о ,z i , ..., z - ,т ) E ^- .      (53)

k =i

Четвёртое и шестое слагаемые взаимно уничтожаются. В пятом слагаемом Z = = [К / X_i ( z - ( Ет ) + П - ( т )) Е ^- ] . Отсюда и из свойства полилинейности следует, что

∞

Е h m ^{( Z}, ..., ^Z,ET ) = m =2

∞ k

= Е Е Е   h m ( X i . ,-.,x i m ) E ^k +

∞

⁺ E G - ^{( X} i ,...^,X - - 1 ^,т ) ^{E -} , - =2

где xi может равняться либо zi, либо Пi. Последняя сумма в (53) есть результат разложения в ряд третьей и четвёртой пар слагаемых в предположении о бесконечной дифференцируемости решений Zk (ет) по аргументу.

Подставим (53) в правую часть, а (45) — в левую часть уравнения (44). Приравняем слагаемые при одинаковых степенях параметра ε . Получим с учётом (51):

^у^ = Л(т)Пк(т) + Pk(По, ..., Пk-1 ,т), dτ

П к (0) = -Z k (0) , к = 1 , 2 , ..., (54)

где P _k (П о , ..., П _{k -} 1 ,т ) — известные операторы от П _о , ..., П _{k -} 1 .

Уравнения (38), (49), (51), (54) полностью определяют формальное решение (40) задачи (36), (37).