Математическое моделирование процесса фильтрации флюидов нефтяного пласта, Усть-Балыкского месторождения

Математическое описание процессов разработки нефтяных залежей имеет своей целью предсказание локальных и интегральных характеристик пластовой системы при различных условиях воздействия на нее и нахождение оптимальных режимов эксплуатации месторождений.

При разработке систем управления технологическим процессом добычи нефти ставятся задачи разработки моделей пласта и выбор наиболее подходящего режима работы оборудования. Процесс развития математического моделирования тесно связан с развитием вычислительной техники. Использование вычислительной техники позволило во много раз ускорить процесс исследования механики разработки нефтяного месторождения. Моделирование, в свою очередь, играет огромную роль при разработке модели нефтенасыщенного пласта [1, 3].

Преимуществом математических моделей является возможность их использования для проведения контролируемых экспериментов, что может быть крайне затруднительно, с реальной системой. Кроме этого, моделирование может применяться для изучения пласта, содержащего как одиночные скважины, так и группу скважин. Использование группы скважин позволяет представить исследуемый объект в виде многомерного или распределенного, что может дать более подробную информацию о процессах, происходящих в нем, и позволит исследовать его свойства, с характеристиками взаимодействия флюидов между собой.

Следует отметить, что за время эксплуатации нефтяного месторождения, в пласте происходит перемещение большого объема жидкости от одного участка к другому. Скважины располагают так, чтобы можно было контролировать процесс движения флюидов. Построение рабочей математической модели позволяет найти место вытеснения нефти рабочим агентом, при определенном расположении нагнетательных скважин.

При моделировании нефтенасыщенного пласта, он разбивается на участки, представляющие собой ячейки. К каждой ячейке присваиваются свойства месторождения. Пласт представляет собой плоскость с точками, которые являются скважинами. Расстояние между скважинами является размерами ячеек [6].

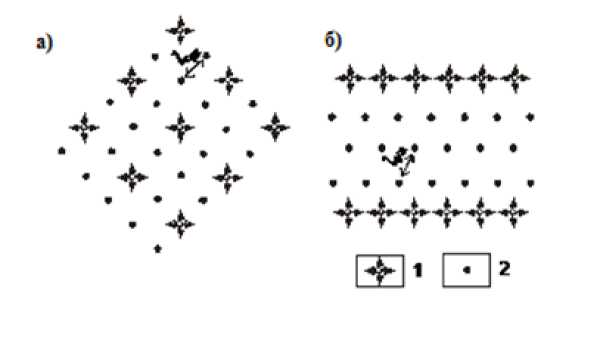
Рисунок 1. Равномерное расположение скважин: а) площадное; б) с разрезанием залежи на блоки. Где: 1 – нагнетательные скважины; 2 – добывающие скважины.

Математическое описание процессов разработки нефтяных залежей имеет своей целью предсказание локальных и интегральных характеристик пластовой системы при различных условиях воздействия на нее, нахождение оптимальных режимов эксплуатации месторождений.

Основные уравнения получаются из следующих физических законов:

• а)    сохранения массы;

• б)    сохранения моментов;

• в)    сохранения энергии (первый закон термодинамики);

• г)    закон Дарси – уравнение движения жидкости;

• д)    уравнения состояния.

При этом, одним из важнейших физических явлений, при разработке месторождения, является движение флюидов в пористой среде, которое определяется законом Дарси. Так скорость фильтрации однородной жидкости в пористой среде прямо пропорциональна градиенту гидравлического давления и площади сечения, перпендикулярной к направлению потока, и обратно пропорциональна ее вязкости [3].

к / dp dz\

^ =--1 v— + — , где

" pv \ d s ds J

• ^    – массовая скорость в направлении потока s;

• k    – проницаемость для однородных флюидов;

• µ    – динамическая вязкость;

• p    – давление;

• z    – вертикальная координата;

• v    – удельный объем.

  

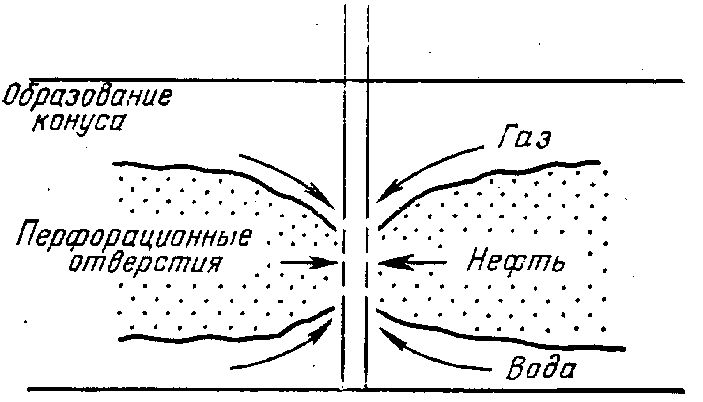
  Рисунок 2. Приток флюида к скважине.

  
  

Модель, рассматриваемая в статье, представляет собой залежь пласта БС6 Усть-Балыкского месторождения [5].

Геометрические характеристики нефтяного месторождения представлены в таблице 1.

Таблица 1.

Геометрические показатели нефтяного месторождения, в метрах.

L x	L y	L z2	L z3
2000	2000	3,4	3

Процессы, происходящие в пласте, зависят от времени. При помощи дифференциальных уравнений в частных производных решается задача фильтрации флюидов [5].

dH2(x,y,z,T) 1 dr т)

д2Н2(х,у,г,т)

2^ дх2

д2Я2(х,у,г,т)

2'у ду2

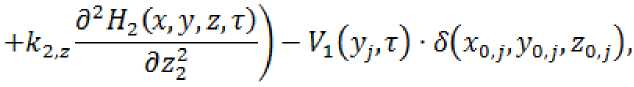
О < х < Lx,0 <у< Ly,Lz2  О

где H i - напор в i -ом изучаемом горизонте ( i =2,3);

k_tx , kt y , ki z — коэффициенты фильтрации по пространственным координатам в горизонте i -ого пласта ( i =2,3);

П - упругоемкость пласта ( i =2);

У^,т) - понижение напора, вызванное воздействием j-ой добывающей скважиной;

6(x oj , yo j, z₀ j ) - функция, равная единице, если x=x₀ j , y=y₀ j , z=z₀ j , и равная нулю в других случаях;

x, y, z - пространственные координаты;

т - время.

Скорость фильтрации нефти по осям представлена следующими уравнениями (закон Дарси):

кгхШг (х,у,я,т)

«2 =----,

/^2

О < У < Ly, L_z3< я <  L_z2,t > 0;

к₂._удН₂(х,у,г,т)

^2 =-------яJ

0 < х < L„.    < z <> 0;

^2^5^2 (^У,^,Т)

^2 =---.

/^2®

0 < х < Lxl0 < у < Lv,t > 0.

Скорость фильтрации воды по осям представлена следующими уравнениями:

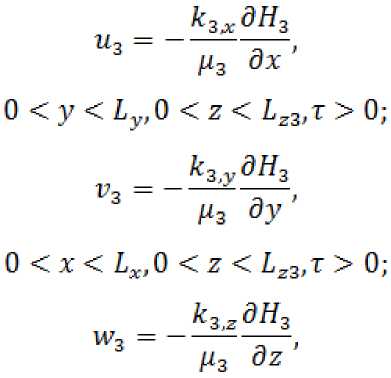
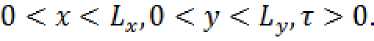
Боковые границы

дЯ2(О,у,г,т) _ о дН2 (Lx,y,z,T) дх         ' дх

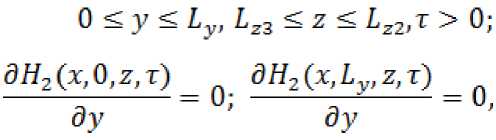
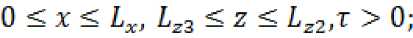
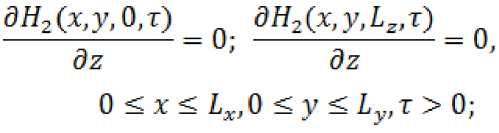
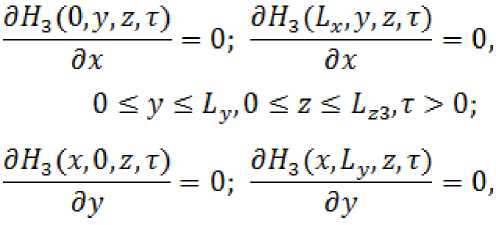
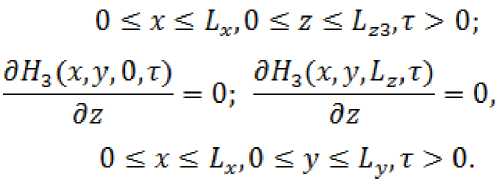
Для решения данной математической модели нефтяного месторождения составим дискретную модель объекта уравнения.

Для решения данной задачи наиболее целесообразно использовать метод конечных разностей. Это, как правило, требует замены вещественных переменных x, y , z, т их целочисленными аналогами. Далее производится дискретизация (см. рис. 3 - 4) и численное решение системы уравнений.

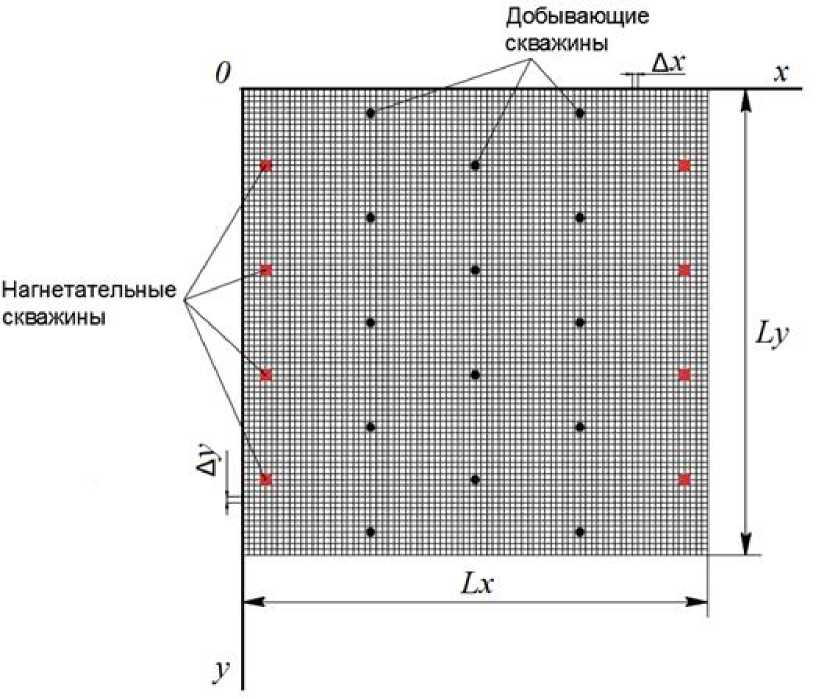
Рисунок 3. Дискретизация объекта по осям x и y .

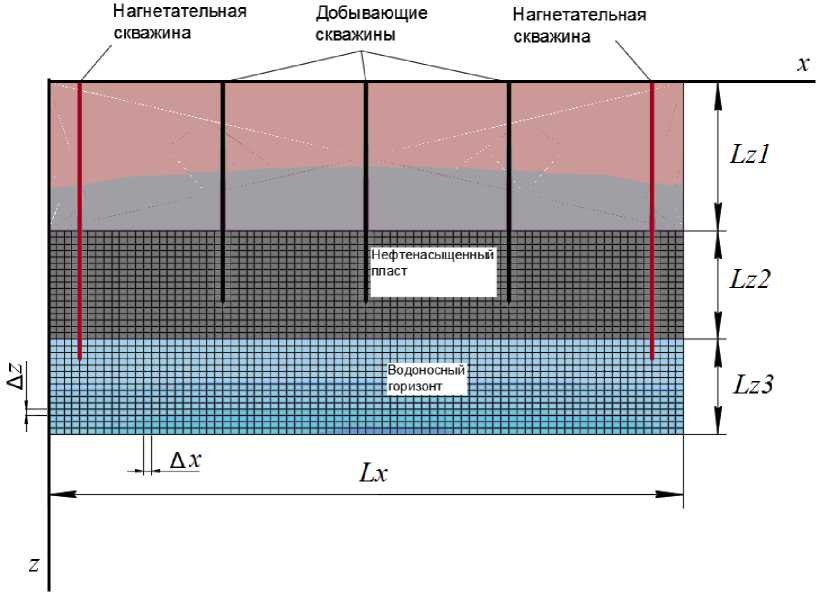
Рисунок 4. Дискретизация объекта по осям x и z .

В результате решения определяются параметры передаточной функции объекта для последующего синтеза системы управления. При этом основными выходными данными модели является дебит, который может быть получен как по отдельной скважине, так и по всему пласту, отображающий продуктивность пласта при определенном режиме эксплуатации.

Недостаток информации о пласте и происходящих в нем процессах для каждой конкретной скважины создает определенные проблемы при построении полноразмерной модели. Из этого следует, что от модели необходимо отображение показателей, которые устойчивы к вариациям исходных данных.

Эффективность разработки нефтяного месторождения характеризует коэффициент извлечения нефти из месторождения. Этот коэффициент равен отношению количества извлеченной нефти к её запасам в пласте. Значение этого коэффициента показывает рентабельность и экономическую эффективность нефтяного месторождения.

Практическая ценность непрерывно действующей динамической модели состоит в постоянном расчете и идентификации параметров объекта в реальном масштабе времени, что даёт возможность использовать полученную модель в системе управления добычей нефти без значительных экономических затрат, и позволяет оптимизировать процесс разработки месторождения и , одновременно, повышает экономическую эффективность процесса эксплуатации месторождения. Целесообразность использования таких моделей напрямую связана с применяемыми методами анализа и синтеза. Применение методов синтеза систем с распределенными параметрами [4] даёт наибольший объем данных для определения значений параметров распределенного регулятора [2], который напрямую влияет на эффективность эксплуатации выбранного месторождения.