Математическое моделирование процесса формообразования песчано-смоляных смесей

спечивает получение отливок с требуемой структурой и, соответственно, с необходимым уровнем технологических свойств.

Большее качество отливок дает литье в песчано-смоляные формы (ПСФ), в которых сочетаются высокая газопроницаемость и прочность, они не сопротивляются усадке, не впитывают влагу застывающим сплавом и не склонны к осыпаемости. Также они с малыми энергозатратами разрушаются после формирования отливки. Это обеспечивает получение отливок, обладающих высокой чистотой поверхности и размерной точностью, а также большую экономию формовочных материалов (по сравнению с песчано-глинистыми формами более 50 %). В свою очередь, уменьшение оборота формовочных материалов значительно снижает расходы по внутризаводской и внешней транспортировке. При использовании литья в оболочковые формы увеличивается выход годного [1-3].

Однако один из недостатков этого способа литья - относительно высокая стоимость связующего. Одним из направлений снижения расхода связующего является использование одновременно с нагревом смеси для формообразования оболочки и статической нагрузки [4, 5]. Другим направлением снижения расхода смеси в целом и связующего в частности служит пределение зависимости свойств оболочковой формы от технологических параметров, что будет способствать управлению свойствами формы, снижению брака и т.п.

Цель настоящего исследования - разработка матматических зависимостей для оперативного управления свойства оболочковой формы.

Ранее [6] было определено напряжение релаксации σ р песчано-смоляной смеси:

Г

£ =

V

2 ■ Т -----1 ■ e

E 0

^

■ 7 + (2-^1 )■ 7 = 7 ■

V E 0 7

2- т - t

2- ^- ■ (1 - e ^Т )

E 0

Формула (1) является уравнением ползучести ПСС в условиях формообразования со статической нагрузкой.

_ Е0 • E1 •£ p °p = 2 •(E о + E), где Е0, Е 1 - соответственно модуль упругости, в момент времени t=0 и t=t1; Ер - деформация релаксации.

Сравнение теоретических и практических результатов приведено на рис. 1.

На графике показана экспериментальная линия регрессии (кривая 1).

Расчетная линия регрессии (кривая 2) построена по уравнению y=-16,667x2 + 4,6333x + + 0,008 с коэффициентом достоверности R2 = 0,9799.

Таким образом, нелинейность деформации ПСС обусловлена различным характером зависимости упругой, вязкой и пластической деформации от напряжения. Получено уравнение ядра ползучести ПСС.

Также была определена формула количества теплоты Q (2), расходуемой на нагрев оболочки:

Q = 5 ■

n = к

Т - Т 0) / X n=0

⁴ ■ z n

nn

+ 52 ■

( n = к 1

Т - Т0) / X—

V n = 0 ^a n - 1

+ ^ + 1 /3■ п-dn )'

A, an      4    J.

где 5 1 , 5 2 - коэффициенты распределения, зависящие от преобладания конвекции или теплопроводности; d – диаметр в точке соприкосновения частиц твердой фазы; z 1 – диаметр (высота) одной песчинки; Т_к и Т 0 - температура подмодельной плиты конечная и начальная; X - теплопроводность дисперсной среды; а 2 – коэффициент температуропроводности.

На коэффициенты распределения влияет степень уплотнения, форма и размер частиц твердой фазы и другие факторы. В реальных условиях можно принимать за сферическую форму песчинок, учитывать пористость и процентное соотношение смолы и кварцевого песка. С уменьшением пористости смеси уменьшается значение конвективного теплообмена и ^коэффициент δ 2 уменьшается.

Очевидно, что повышение истинной плотности в процессе термического воздействия приведет к увеличению скорости прогрева формы, т. е. к сокращению тепловых потерь. Приложение статической нагрузки в начальный момент нагрева дисперсной смеси приводит к повышению ее плотности [7].

Следует учитывать и то, что по мере плавления смолы (а также увеличения статической нагрузки на формирующуюся дисперсную смесь) смола заполняет поры и твердеет, схватывая песчинки. Здесь уже будет происходить передача тепла теплопроводностью. Для такого состояния значение λ будет также зависеть от соотношения связующего и песка.

В формуле (2) ΔT для конкретных случаев есть величина постоянная, массу смеси можно представить как произведение объема v на плотность р. Объем дисперсной смеси есть произведение площади S на высоту z. Площадь определяется геометрическими размерами модельной нагреваемой плиты, а высота есть толщина оболочковой формы (величина прогрева и твердения формы). Толщину стенки формы z можно вычислить по формуле z = k • Т?, (3)

где k – коэффициент пропорциональности; τ – время теплового воздействия на дисперсную песчано-смоляную среду [8].

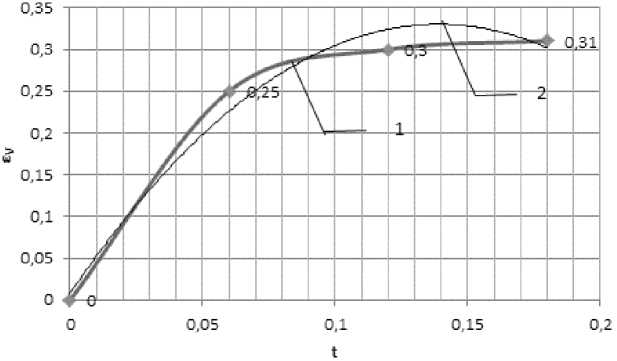
Рис. 1. Сравнение теоретических и экспериментальных данных деформации ПСС во времени

Fig. 1. Comparison of theoretical and experimental data of SRM deformation in time

Таким образом, можно получит зависимость тепла, идущего на нагрев песчано-смоляной смеси, от времени теплового воздействия на эту смесь:

Q = c ⋅ ΔТ ⋅ ρ ⋅ S ⋅ k ⋅ τ . (4)

В правой части формулы все значения кроме времени есть постоянные (можно изначально задаваться различными температурами нагрева смеси и площадью, подвергаемой термическому воздействию).

Полученную зависимость можно использовать для определения времени нагрева смеси, необходимого для образования оболочковой формы.

На рис. 2 представлена зависимость количества теплоты от времени нагрева (экспериментальные данные и данные расчета по полученной формуле, эксперименты проводили в цехе коркового литья ТОО «КМЗ имени Пархоменко», г. Караганда, Казахстан) при температуре нагрева модельной плиты 250 °С.

Очевидно, что выделение теплоты происходит по закону, близкому к параболическому. Для мелких и средних отливок оптимальная толщина песчано-смоляной оболочки составляет 8-10 мм, для обеспечения такой толщины необходим нагрев смеси в течение 25-30 с. Уменьшение толщины оболочки приведет к разрушению формы при заливке, а увеличение толщины – к перерасходу смеси и ухудшению ее газопроницаемости. Дальнейшее время нагрева нецелесообразно, так как интенсивность выделения теплоты для прогрева формы уменьшается, к тому же происходит выгорание смолы, что разупрочняет форму. Расхождение между экспериментальными и расчетными данными составляет 5-7 %.

Таким образом, получена зависимость количества теплоты от времени теплового воздействия. Теоретические и экспериментальные исследования показали, что для получения качественной оболочки необходимо нагревать песчано-смоляную смесь в течение 25-30 с при температуре 250 °С. В случае увеличения продолжительности или температуры нагрева происходит разупрочнение формы за счет выгорания связующего (смолы).

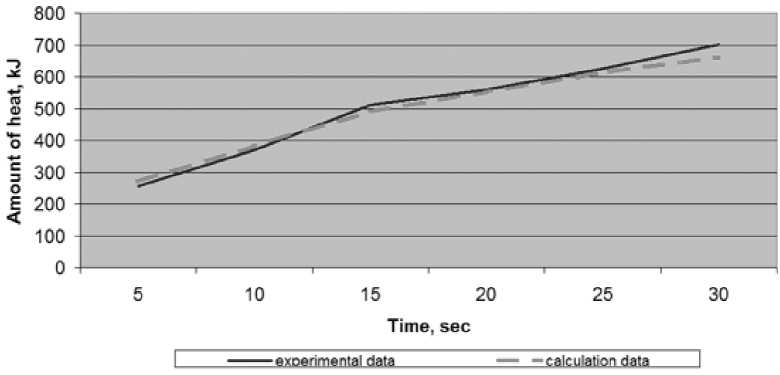
Рис. 2. Зависимость количества теплоты от времени нагрева смеси

Fig. 2. The heat quantity depends on the heating time of the mixture

Пористость песчано-смоляной смеси можно рассчитать по следующей зависимости:

, d ² х S ² x F xK p x т

m = 1------

96 x Q x h x n

Q

– объем газа, проходящего через образец поперечного сечения F и высоты h за время τ при перепаде давлений ^p ; d - диметр зерна; S - площадь просвета между частицами смеси; m – пористость смеси; η – динамическая вязкость газа.

Плотность можно определить по (6):

р =

M x в

ln

—--Mx»n

| 1 Г

P1 xl--x ln^Pnp -H v a I    Fx(HL )JJ где M – масса уплотняемой смеси; β – параметр, учитывающий влияние внешнего трения; F – площадь прессующего органа; рпр - предельная плотность сплошного тела; Н - начальная высота заполнения формы; L – расстояние, пройденное прессующей колодкой при прессовании формы; ρ – плотность смеси при давлении 0,1 МПа; α – коэффициент потери сжимаемости; 1,

μ – коэффициент уплотняемости.

Полученная формула дала хорошую сходимость расчетной и практической величины плотности смеси (рис. 3). На оси абсцисс показано первоначальное значение давления.

По результатам исследований была разработана программа расчетов технологических параметров в зависимости от габаритов опоки, температуры и давления на смесь. Интерфейс программы и результаты вычислений представлены на рис. 4, 5.

На базе проведенных теоретических исследований напряженно-деформированного состояния составлена программа расчета технологических параметров изготовления песчаносмоляной формы.

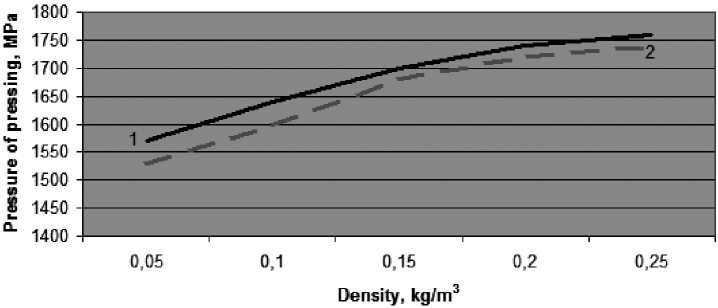
Рис. 3. Расчетная и практическая плотности ПСС в зависимости от давления прессования (1 – теория, 2 – эксперимент)

Fig. 3. Influence of pressing pressure on SRM densities (1 – theory, 2 – experiment)

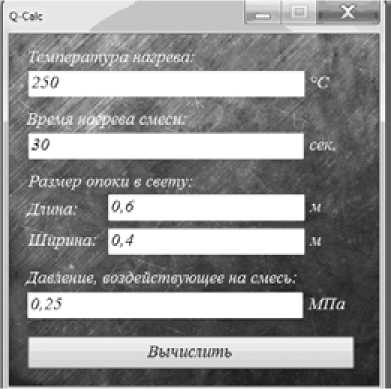
Рис. 4. Пример ввода начальных данных

Fig. 4. Example of initial data introduction

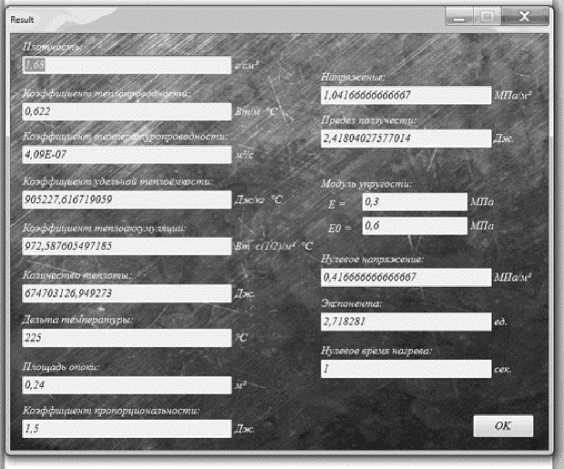
Рис. 5. Результаты вычислений

Fig. 5. Calculation results interface