Математическое моделирование процесса литья деталей газотурбинных двигателей
Автор: Дубровская Александра Сергеевна, Донгаузер Константин Александрович, Труфанов Николай Александрович
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Рубрика: Технологии в авиационном и ракетно-космическом комплексе
Статья в выпуске: 4-5 т.14, 2012 года.
Бесплатный доступ
Рассматривается применение компьютерного моделирования к процессу изготовления отливок деталей машин методом литья по выплавляемым моделям (ЛВМ). Построена математическая модель, описывающая процессы заливки расплава в керамическую форму с последующим его затвердеванием. При помощи термометрирования реального производственного эксперимента проведена верификация полученной модели.
Математическое моделирование, компьютерная имитация, литье по выплавляемым моделям, кристаллизация
Короткий адрес: https://sciup.org/148201400
IDR: 148201400 | УДК: 519.6
Текст научной статьи Математическое моделирование процесса литья деталей газотурбинных двигателей
точной неразъемной разовой модели, по которой из жидких формовочных смесей изготовливается неразъемная керамическая оболочковая форма. Перед заливкой расплава модель удаляется из формы выплавлением, выжиганием, растворением или испарением, для удаления остатков модели и упрочнения форма может быть нагрета до высоких температур, что улучшает ее заполняемость расплавом [2]. Для формирования внутренней полости изделия используется керамический стержень.
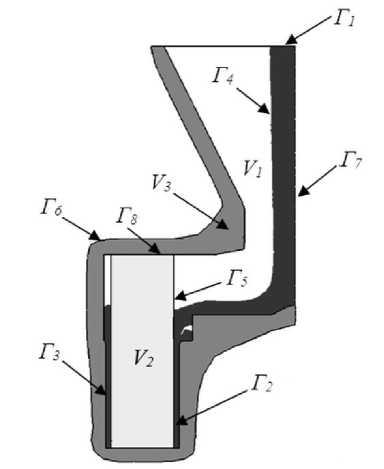
Рис. 1 . Схематическое изображение процесса изготовления отливки изделия методом ЛВМ:
V1 – область тела отливки, V2 – стержень, V3 – форма, Г1 – граница для заливки металла, Г 2 – граница контакта стержня и металла, Г3 – граница контакта металла и формы, Г4 – свободная поверхность металла, Г5 – свободная поверхность стержня, Г 6 –свободная поверхность формы, Г7 – плоскость симметрии
После заливки расплава в керамическую форму происходит охлаждение системы, в процессе которого расплав кристаллизуется, принимая все конфигурации керамической формы. Затем форму разрушают, керамический стержень вытравливают, отливку очищают, обдувая ее воздухом под давлением. Удаляют лишний металл (прибыли).
Составим математическую модель для описания производства отливки детали методом точного литья. На рис. 1 изображена схема изготовления полой отливки, включающая керамическую форму, стержень и область формирования отливки.
Исследование нестационарных температурных полей в расчетной области при заливке металла и кристаллизации отливки ведется с помощью дифференциального уравнение теплопроводности
P i " T + P i U ' gradT = V ( A V T ) x e V i
ОT Gt где энтальпия материала отливки
T
HST) -JCp, (T)dT + L[1 - gs (T)]
0 , для материала формы и керамического стержня дифференциальное уравнение теплопроводности имеет вид
P i—i -tx-vAV T ) x e v i
о T дt
T
Hi(T) -f c„(T) dT где индексы: 1, 2 и 3 относятся к областям V1, V2 и V3 соответственно, T - температура; t - время; р - плотность материала; ср - удельная теплоемкость; L - удельная теплота фазового перехода; X=X (Т) - коэффициент теплопроводности; U -(иуи2,и3) - вектор эффективной скорости расплава, рассчитываемый через истинную скорость жидкой фазы U. следующим образом: U - gl' U.; gl - доля жидкой фазы; gs - доля твердой фазы gs =1 - gi; x = (x1,x2, x3) - радиус-вектор в декартовой системе координат.
Уравнение теплопроводности дополняется граничными условиями на поверхности контакта форма - отливка и отливка - стержень.
a T _ a T
- A - A ^- a ii( T i - T )
оn оn x e Г, i -i,2 .
На границах теплообмена с окружающей средой условия имеют вид
A — - -a ( T - T ) - a ( T 4 - T 4 ) i ic i c i c
оn i - <
i,
2,
x e Г 4 x e Г,
5 ,
[ 3, x e Г 6
где a(t) - коэффициент теплоотдачи, определяемый в соответствие с [3], индекс с соответствует параметрам окружающей среды, е - степень черноты, а а - постоянная Стефана-Больцана. Начальные условия накладываются на температуру заливаемого металла и формы с керамическим стержнем T ( x ,0) - Tof ( x), i - 1,2,3; x e V .
Для моделирования заливки расплава в керамическую форму и расчета тепломассоперено-са используется дифференциальное уравнение движения. В расчетной области рассматривается неизотермическое ламинарное течение несжимаемой ньютоновской вязкой жидкости. Граница раздела фаз явным образом не выделяется.
P ^У- + — grad ( U 2) + 2 p( rotU x U ) - дт 2
- - P i g + grad ( p ) + grad p dix ( U ) + ^ U
K
,
x e V , g - ускорение свободного падения; p -давление; p - коэффициент вязкости; K - проницаемость дендритного каркаса, рассчитываемая g 3
по формуле Кармана-Козени: K - —1 2 , здесь kSV
S - 6(i - gl) - удельная поверхность твердожид-VD кой фазы, D - характерный размер дендрита, к -постоянная Кармана, к=5.
Уравнение движения дополняется эволюционным уравнением неразрывности сжимаемой среды в области жидкой фазы, для соблюдения закона сохранения массы:
^^ + div (p U) - 0, _ v д t v 0 ’ , x e Vi
.
Уравнение движения дополняется следующими граничными условиями: U - о при x e Г2 и Г3 - условие полного прилипания вязкой среды к твердой поверхности; су • n - p при x e Г4 - условие отсутствия касательных (рт - 0) и равенство нормальных напряжений давлению газа над свободной поверхностью (pn = -pcn ), n – единичная нормаль к свободной поверхности отливки.
Форма свободной поверхности Г 4 определяется во времени через зависимость нормальных напряжений и поверхностного натяжения в металле при x е Г 4 , по механизму, предложенному в [4]. На границе Г 2 ^ Г з для кристаллизовавшегося металла скорость U автоматически становится равной 0, поскольку U = g l • U 1 , а g l =0. Предполагается, что в начальный момент времени на поверхности x е Г 1 существует источник расплава, для которого известно начальное распределение скоростей: U 0 = ( 0,0, и 0 ) .
Для верификации предложенной математической модели на опытном заводе ОАО
«Авиадвигатель» был проведен эксперимент по изготовлению монокристаллических образцов из никелевого суперсплава. В ходе работы использовалась специальная вакуумная печь подогрева форм. Заливка двух блоков с образцами производилась в предварительно нагретую керамическую форму. После выдержки образцы постепенно выдвигались из печи, чтобы обеспечить плоский температурный градиент, противоположный направлению роста кристаллов. Задание начальных и граничных условий при математическом моделировании соответствовало технологическому режиму производства образцов. На рис. 2 изображен процесс заливки образцов во времени. Полученная картина соответствует инженерным представлениям о заполнении керамической формы расплавом.
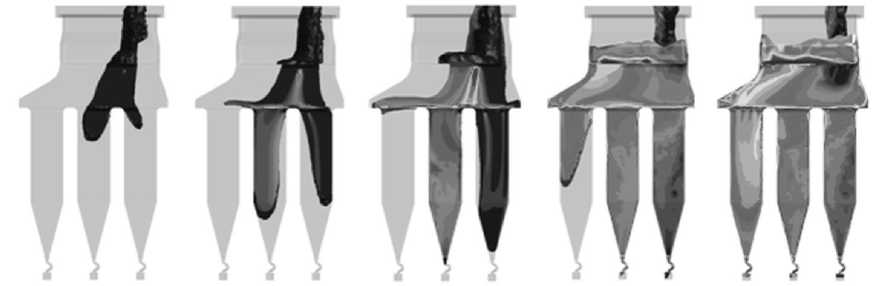
Рис. 2. Результаты компьютерного моделирования процесса заливки образцов из жаропрочного никелевого суперсплава
При проведении натурного эксперимента в керамическую форму и полость отливки были установлены специальные температурные датчики под номерами №7-№12 (схема установки термопар показана на рис. 3а). Термопары с четными номерами передавали данные о температуре в керамической форме, а с нечетными – в отливке. Полученные данные были интерполированы в кривые, показывающие температурновременную зависимость в форме (рис. 3б) и отливке (рис. 3в). Данные кривые были сопоставлены с результатами компьютерного расчета в узлах, соответствующих схеме расположения датчиков. На рис. 3б и 3в приведено сравнение с расчетными данными показаний термопар №11 и №12 соответственно. Абсолютная погрешность для математической модели не превысила 10°С, что в интервалах температур кристаллизации составляет менее 1%.
Выводы: подтверждено соответствие результатов численного моделирования экспериментально полученным данным, что свидетельствует о возможности широкого применения математического моделирования для имитации процессов ЛВМ.

a)
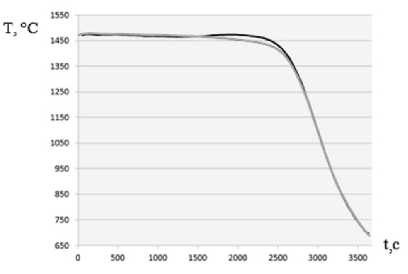
б)
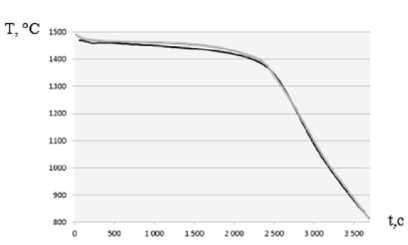
Список литературы Математическое моделирование процесса литья деталей газотурбинных двигателей
- Монастырский, А.В. Разработка технологии литья крупногабаритных лопаток ГТД для энергетических установок с применением систем Полигон и ProCAST/А.В. Монастырский, В.П. Монастырский, Е.М. Левитан//Литейное производство. 2007. № 9. С. 29-34.
- Степанов, Ю.А. Технология литейного производства/Ю.А. Степанов, Г.Ф. Баландин, В.А. Рыбкин. -М.: Машиностроение, 1983. 287 с.
- Дубровская, А.С. Численное исследование влияния технологических и конструкционных параметров на процесс изготовления монокристаллических отливок деталей газотурбинных двигателей/А.С. Дубровская, К.А. Донгаузер//Вестник ПГТУ Прикладная математика и механика. 2011. №9. С. 81-102.
- Brackbill, J.U. A continuum method for modeling surface tension/J.U. Brackbill, D.B. Kothe, C. Zemach//Journal of Computational Physics. 1992. №100. P. 335-354.


