Математическое моделирование процесса получения цилиндрических спаев стекла с металлом

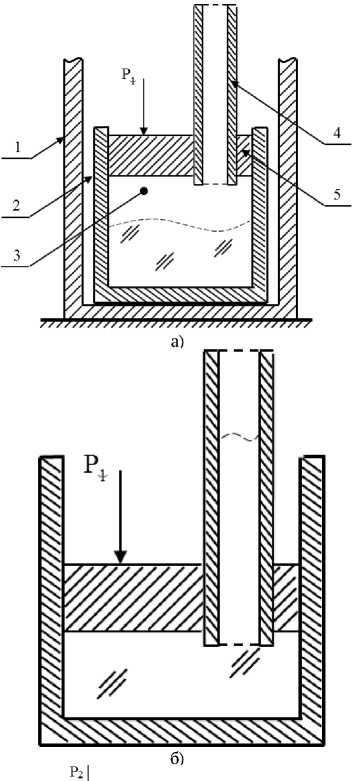
термической печи 1 устанавливается тигель 2 со стеклянной шихтой. При определенном температурном режиме шихта расплавляется, образуя вязкую однородную стекломассу 3. Через поршень 5 с отверстием для образца 4 передается давление Р1, которое позволяет выдавить вязкую стекломассу внутрь образца (рис. 1б). После заполнения стекломассой определенного объема начинается охлаждение экспериментального образца, в процессе которого на его верхний то- рец, с целью создания определенного уровня напряжений, подается давление P2.

В данном технологическом режиме моделированию подлежат следующие параметры: Tw ‒ температура размягчения стекла, при достижении которой начинает подаваться давление; Р ‒ давление; η ‒ вязкость стекла при температуре Тw; V ‒ свободный объем внутри образца до эксперимента; t1 ‒ время, за которое при данных параметрах стекломасса заполнит весь свободный объем, эволюция напряженно-дефор-мируемого состояния экспериментального образца в процессе охлаждения при           .

Математическая модель. Для определения параметров технологического режима разделим задачу на две несвязанные:

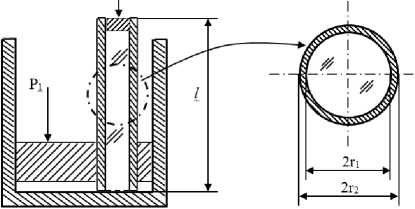
• -    стационарного течения вязкой жидкости по трубе круглого сечения (одинакового вдоль всей длины трубы),             , T w = const (рис. 2);

• -    определения термических напряжений и деформаций в экспериментальном образце стеклометаллоком-

• позита в процессе остывания,            , темпера

тура зависит от времени T(t) (рис. 2).

Первая задача в случае параллельного течения вязкой жидкости между неподвижными стенками носит название пуазейлевого течения и при определенных допущениях имеет аналитическое решение [3]. Для трубы кругового сечения аналитическая зависи- мость скорости течения в зависимости от давления, характерного размера и вязкости имеет вид:

р=^(Я²-г²) ^1

где ‒ скорость течения жидкости; ΔP ‒ разница давлений между верхним и нижним торцами образца; l ‒ длина образца; R ‒ внутренний радиус образца; r ‒ текущий радиус.

Масса Q вязкого стекла, протекающего в 1 секунду через поперечное сечение образца равна

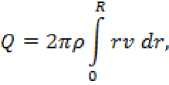
где Q ‒ масса вязкого стекла; ρ ‒ плотность стекломассы, тогда время заполнения свободного объема V стекломассой вычисляется по формуле:

V itR2l           R2l tw op ~

V 2np rv dr 2 rv dr

Задача может быть существенно усложнена предположением, что при заполнении стекломассой металлического цилиндра ее вязкость изменяется по высоте.

в)

Рис. 1. Схематичное изображение установки для создания экспериментальных образцов СМК стержней: а) принципиальная схема установки - 1 ‒ корпус печи; 2 ‒ тигель; 3 ‒ стекломасса; 4 ‒ образец; 5 ‒ поршень; б) процесс постепенного заполнения образца; в) полностью заполненный стекломассой образец, с установленным на стеклянном торце поршнем 6 для передачи давления P 2

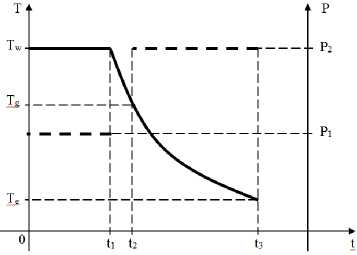
Рис. 2. Режим изменения температуры и давления: T w – температура размягчения стекла; T g – температура стеклования; T e – температура среды

Исследование термических напряжений СМК заключается в определении напряженно-деформи-руемого состояния в составном цилиндре при изменении температуры. Предположение, что напряжения не оказывают существенного влияния на температуру, позволяет решать последовательно следующие задачи: задачу определения температурных полей в материале; краевую задачу определения напряженно-дефор-мируемого состояния для слоистого материала с температурными и структурными неоднородностями.

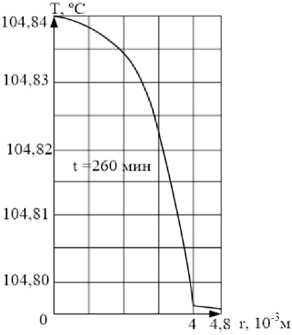
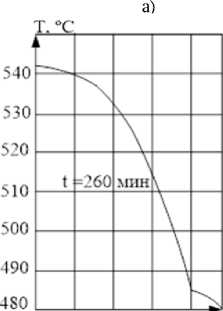
0                   4 4.8 r. 10'³m

б)

Рис. 3. Пример распределения температурных полей в СМК в фиксированный момент времени: а) при d < 80·10^-3 м; б) при d > 80·10^-3 м

Определение полей температуры для слоистых материалов заключается в постановке краевой задачи теплопроводности, с учетом изменяющихся теплофизических характеристик и условием идеального контакта на границе разных материалов и равномерного нагрева вдоль образующей [5]. Результатом решения температурной задачи являются пространственновременные поля распределения температуры T(r, t), с учетом которых далее решается задача определения напряжений и деформаций. Решение температурной задачи показало, что для диаметров образцов d < 80·10-3 м температура незначительно изменяется по диамет- ру композиционного стержня и ее можно считать не зависящей от радиуса (рис. 3), что позволяет сделать предположение о том, что в целом температура внутри стержня может быть задана как температура режима, т.е. Т = Т(t).

Математическое моделирование охваты-вает временной период от момента перехода стекломассы в стеклообразное состояние Tg до полного остывания стеклометаллокомпозита (см. рис. 2). Считаем, что стекло находится в упругом состоянии, а металлическая оболочка при достижении определен-ного уровня напряжений - в состоянии упругопластического деформирования. Деформирование двуслойного цилиндра в процессе остывания является следствием разницы механических характеристик материалов и давления на стеклянный сердечник распределенного по верхнему торцу (рис. 1в). Геометрия цилиндра позволяет сделать предположение о осесимметричной деформации цилиндра. Поэтому краевая задача механики в упругой области состоит из уравнений равновесия записанных в цилиндрической системе координат

^°тг | ®°zt | °rr — °ФФ _ Q dr dz r da do a f 4B ^^      46146» —^ f 4b   dr dz r              (4)

соотношений Коши dur       ur       duz err =      ефф = ~' ezz =

_ 1 /ди2 1 dur\ гя 2 \ dr "^ r dz / уравнений состояния

/du, u, du dr

dz t du„

+2^^

dr adT,

0 du, u, du аФФ dr

dz

+2д--(ЗЛ + 2д) I adT,

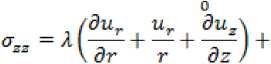
du             f

+2p.— —-(ЗЯ + 2д) adT, dz             J

0 Su dz гдн σrr, σzz, σφφ, σzr, err, ezz, eφφ, ezr, ur, ur ‒ компоненты тензоров напряжений, деформаций и перемещений, соответственно, отличные от нуля вследствие предположения осесимметричной деформации и являются функциями от координат r (радиус), z (длина), t (время); α ‒ коэффициент линейного температурного расширения,

λ, μ ‒ параметры Ламе, зависящие от механических свойств материала. Поскольку в нашей задаче рассматривается двухслойный цилиндр, выполненный из различных материалов (см. рис. 1в), механические характеристики для 0≤ z ≤ l имеют вид:

_ ( a_g(t),X_g(t),g_g(t), 0 < r < r_v ^(ОДтСО^^СО-П <  r < r₂.

Краевые условия на границе сопряжения двух разных материалов записываем, предполагая, наличие идеального контакта:

^rr(.rl ~ O,Z,t) = СТГГ(Г! + O,Z,t), u^ - O,z,t) = ur(rt + O,z,t).  (7)

Краевые условия на внешней боковой поверхности и на торцах запишем, учитывая равномерно распределенное давление на стеклянный сердечник со стороны верхнего торца, и отсутствие нагрузки на внешней поверхности цилиндра и на нижнем торце

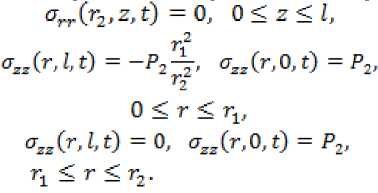
Начиная с некоторого момента времени при охлаждении образца в нем формируются напряжения за счет разницы коэффициентов линейного температурного расширения и модулей упругости первого рода, которые приводят к процессу пластического течения в металлической оболочке. В таком случае уравнения равновесия (4) необходимо интегрировать отдельно в области пластического теченияr e [rvr2] и в области обратимого деформирования r e [o,rt] при усло-

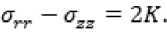
вии

(9) где K ‒ предел текучести.

Отметим, что требование непрерывности этих параметров на границе области пластического течения приводит к необходимости определения поля перемещений не только в области обратимого деформирования, но и в области с накопленными необратимыми деформациями. Распределение предела текучести будем считать известной функцией, линейно зависящей от текущей температуры:

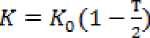
где K 0 – предел текучести при начальной температуре.

Выводы: при относительно простой постановке задачи (4) ‒ (9) следует отметить сложность получения аналитических зависимостей и построения численного решения ввиду наличия разных материалов, их реологических свойств и различного типа деформирования. Используя методы численного интегрирования можно исследовать процесс накопления необратимых деформаций, пользуясь заданным распределением температур и определенного в зависимости от такого распределения предела текучести.