Математическое моделирование процесса прессования труб переменного сечения

Основным параметром, определяющим возможность протекания процесса прессования в стабильных условиях, является максимальное усилие прессования, возникающее в процессе деформации.

При проектировании нового технологического режима прессования труб переменного сечения с утонённой стенкой на заднем участке, важнейшим ограничением является уровень предельно допустимых нагрузок на деформирующий инструмент прессов, входящих в прессовую линию, что объясняется изменением толщины стенки в процессе прессования от номинального до минимального значения. Поэтому очень важно точно прогнозировать величину максимального усилия, возникающего в процессе деформации металла.

Характер течения металла при прессовании определяется рядом факторов, главными из которых являются: калибровка матрицы (HМ, HТМ, ю) и пресс-шлы (DИГтах , dp , LИГтах , Lц , Lр ), положение и форма границ пластического очага деформации (R1, R , r1, r, 6 , в , Y), режимы прессования (vM , Xi), условия трения на контактных поверхностях (тS, ц), механические свойства исследуемого металла (оS) и другие. Действия этих факторов определяют структуру моделируемой системы, свойства ее элементов и причинно- следственные связи, присущие системе и существенные для достижения цели моделирования.

В соответствии с основным законом теории пластических деформаций о течении металла в направлениях наименьшего сопротивления в процессе распрессовки заготовка ( D ₀, d ₀, h ₀) под влиянием силового воздействия P пресс-шайбы осаживается и увеличивается в диаметре ( D К ). Одновременно или несколько позже в зависимости от отношения величины поперечных сечений заготовки и пресс-изделия, длины заготовки и других деформационных условий начинается заполнение прессуемым металлом канала матрицы. Непосредственно с этого момента начинается процесс выдавливания трубы в отверстие одноканальной конической матрицы - стадия прессования трубы.

Для математического описания процесса прессования и решения соответствующей задачи, были приняты следующие основные допущения: деформируемый металл идеально пластичный ^{( т} 5 = ^о s! V3 ) и несжимаем ⁽ ^„ + ^ yy +^ _zz = 0); температура пластической горячей деформации в процессе прессования не изменяется ( A t = 0 ); деформация осесимметричная ( x_y = y_y ); силы контактного трения постоянны и не зависят от нормальных давлений ( т _к =цт S ); температурные на-

Выдрин А.В., Космацкий Я.И., Баричко Б.В.

пряжения и деформации, силы инерции и другие массовые силы пренебрежимо малы.

Математическое описание процесса прессования труб переменного сечения осуществлялось в прямоугольной пространственной системе координат. В связи с тем, что в течение основной стадии процесса различные участки выпрессовывае-мого металла находятся в различных напряженно-деформированных состояниях, претерпевают упругие или пластические деформации, было произведено условное разделение на несколько характерных блоков в соответствии с расчетной схемой, представленной на рис. 1.

В соответствии с рис. 1, границами блоков с соответствующими им параметрами зон пластической деформации при осесимметричном прессовании и выполнении условия несжимаемости являются сферы.

Следует отметить, что одними из характерных, влияющих на условия и результаты прессования, являются зоны 6 и 9, находящиеся вблизи матрицы. Металл в этих зонах на рассматриваемой стадии в истечении не участвует или почти не уча-

Математическое моделирование процесса прессования труб переменного сечения ствует и образует объемы пластически недефор-мирующегося, находящегося в упругом состоянии металла [1, 2].

В очаге деформации, ограниченном блоками 2, 3 и 4, скорость течения металла в некоторой точке по оси z зависит не только от координаты данной точки z , но и от ее положения по оси x . Следовательно, скорость линейной деформации ξ _zz не является постоянной величиной по объему металла. Поэтому для математического описания процесса были определены средние значения скорости линейной деформации ξ _{zz ср} , которые являются средними между скоростью линейной деформации на границах очага деформации, т. е. на границе контакта металла с пресс-иглой и застойной зоной металла:

ξ _{zz ср2} = 12 ν _П ( λ ₂ - 1 ) ×

( cos 0 cos a | x|----------------------+---------I,                  (1)

I R cos Y- R 1 ^cos Ф ^ ИГтах )

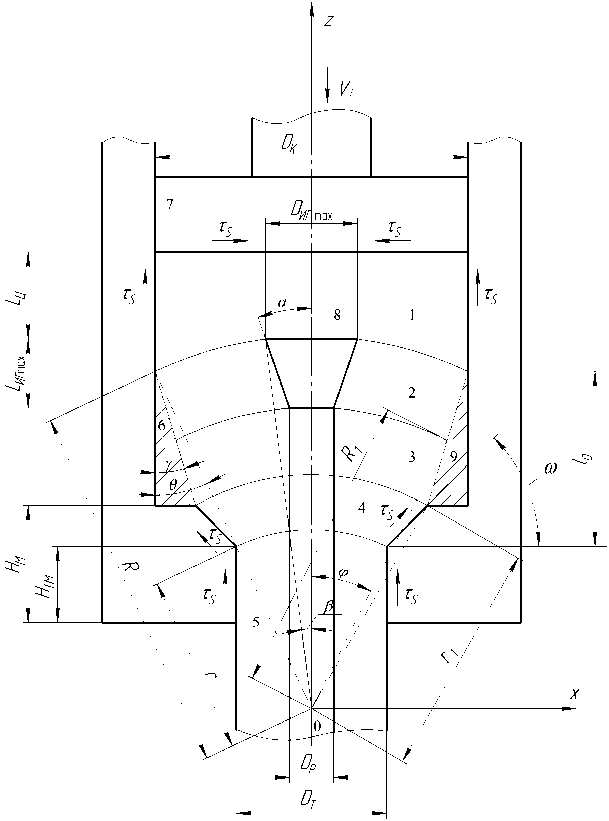
Рис. 1. Расчётная схема процесса на стадии прессования с геометрическими граничными условиями

ξzzср3=12λ2νП(λ3-1)×

-

R cos ^в - L ИГтах к

+

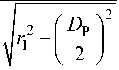
+              cosθ

R 1 cos ϕ- R cos γ+ l 0 - ( H М -

ξzzср4=12λ2λ3νП(λ4-1)×

r 12

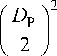
D Р

cos ω

R cos γ- l 0 + ( H М - H ТМ ) - r cos γ

Уравнение баланса мощностей для случая горячего прессования труб с использованием пресс-иглы с коническим участком включает в себя мощность сил деформирования N_P с приложением усилием пресса, мощности сил формоизменения заготовки N _Ф , мощность N _Δ , развиваемую

максимальными касательными напряжениями на всех поверхностях разрывов скоростей S _Δ в заго-

товке и мощность сил контактного трения N _τ .

В общем виде уравнение баланса мощностей представляет собой выражение следующего вида:

NP

=τ S

Г                                  )

JJJ H 2 d + JJJ H 3 dV 3 + JJJ H 4 dV 4

к V 2               V 3              V 4           J

+JJ T$ I Av| dS + JJ TkVcdS , (4) SΔ Sк где τS – сопротивление металла на сдвиг; τк – силы контактного трения на единицу поверхности контакта; Sк – площадь контакта; νс – средняя скорость скольжения по поверхности контакта; H2 , H3 , H4 – интенсивность скоростей деформаций сдвига в соответствующих блоках; V2 , V3 и V4 – объемы металла соответствующих блоков; Δν – разница касательных скоростей к поверхности разрыва перед поверхностью разрыва и за ней; σS – сопротивление металла пластической деформации.

Путем преобразований уравнения баланса мощностей, с учетом всех переменных параметров, получена зависимость для определения усилия прессования, возникающего при изготовлении труб с уменьшением толщины стенки на заднем участке, представленная в общем виде:

p = ^ Ф +2L _O ^Г 1 с +ц у ) , (5)

Vn V3 $ к 4 ^J v 7

где μ – коэффициент трения скольжения; ν П – скорость прессования; B , С – переменные параметры мощности сил контактного трения и мощности, развиваемой максимальными касательными напряжениями на поверхностях разрывов скоростей S _Δ в заготовке соответственно.

Представленная математическая модель (5) была использована для численного исследования влияния изменения величины максимального диаметра пресс-иглы на значение величины усилия прессования. Параметры процесса прессования труб с применением пяти различных профилировок пресс-игл, при неизменных остальных параметрах, представлены в таблице.

Параметры прессования труб ∅89×12 мм переменного сечения из стали марки 08Х18Н10Т

Минимальная толщина стенки трубы ( h Тmin ), мм		11,0	10,0	9,0	8,0	7,0
Размеры заготовки ( D 0 / d 0 × h 0 ), мм		191 / 77 × 474
Геометрические параметры профилировки пресс-иглы, мм	L ИГmax / L Ц / L Р	30 / 100/ 1370
	D ИГmax	69,20	71,20	73,20	75,20	77,20
Диаметр втулки контейнера ( D К ), мм		195
Геометрические параметры матрицы	H ТМ / H М , мм	14 / 25
	ω , град	45
Коэффициент вытяжки ( λ ), мм/мм		9,16	9,87	10,58	11,30	12,0
Температура прессования ( t П ), °С		1180
Скорость прессования ( ν П ), мм/с		220
Коэффициент трения скольжения ( μ )		0,035
Сопротивление металла пластической деформации ( σ S ), МПа		161,9	161,2	160,5	159,8	159,2
Максимальное усилие прессования ( P max ), МН		20,9	21,1	21,4	21,7	21,9

Максимальное усилие прессования, МН

* ^(^ИГтах )    “ *“ ^(^Tmin )

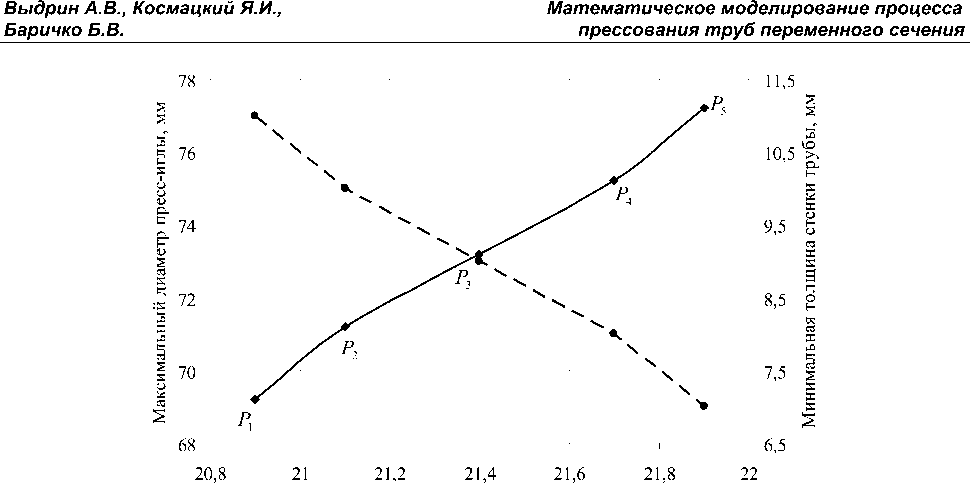
Рис. 2. Зависимость максимального усилия прессования трубы переменного сечения от максимального диаметра пресс-иглы и минимальной толщины стенки: P 1 = 20,9 МН, P 2 = 21,1 МН, P 3 = 21,4 МН, P 4 =21,7 МН, P 5 = 21,9 МН

На рис. 2 представлены построенные в одной системе координат с использованием заданных значений определяющих параметров и расчетных значений параметров отклика графические зависимости изменения значения максимального усилия прессования от максимального диаметра пресс-иглы и минимальной толщины стенки трубы .

В соответствии с графическими зависимостями, представленными на рис. 2, приведено подтверждение фундаментального положения теории прессования [2]. Показано, что значение величины максимального усилия прессования P ₅ = 21,9 МН, возникающего при прессовании трубы с меньшей толщиной стенки (7 мм) на заднем участке, превышает значения величины максимального усилия прессования P ₁ = 20,9 МН, возникающего при прессовании трубы с большей толщиной стенки (11 мм). При этом зависимости изменения параметров отклика от определяющих параметров обратно пропорциональны.

Таким образом, в отличие от опубликованных в работах [3–5] в настоящее время зависимостей для определения максимального значения усилия прессования разработанная математическая модель позволяет, учитывая специфическую профилировку прессового инструмента, прогнозировать возможность изготовления труб заданного сортамента и определять рациональную форму прессового инструмента.