Математическое моделирование процесса снабжения производственного предприятия на основе регистров бухгалтерского учета

Данные научные исследования ведутся в рамках научной школы моделирования и управления сложными системами академика Академии наук Республики Татарстан Т.К.Сиразетдинова [1 - 3], которая развивается в КНИТУ-КАИ. Одним из подходов к задачам планирования и прогнозирования производственных предприятий является применение динамических моделей финансово-хозяйственной деятельности предприятия, в основу которых положена структура бухгалтерского учета [4 - 8].

В представленной работе на основе этих подходов построена более подробная дискретная математическая модель процесса снабжения предприятия, начиная от процесса закупок и до передачи сырья, материалов и комплектующих в производство. Эта модель может быть использована как в решении самостоятельных задач, связанных с процессом закупки сырья и материалов, так и встроена в более общую модель функционирования предприятия.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ СЧЕТА

В основу математической модели предприятия положена математическая модель бухгалтерского счета [4 - 6], которая в алгебраическом виде для активного счета описывается уравнением (1), а для пассивного счета уравнением (2):

S(t) = S(t - At) + DT(t) - CT(t), (1)

где: S(t) – сальдо счета на текущий момент времени,

S(t– Δ t) – сальдо счета на предыдущий момент времени,

DT – оборот по дебету,

CT – оборот по кредиту,

∆t – интервал времени, соответствующий рассматриваемому периоду, t – текущий момент времени.

Разница между активным и пассивным счетом обоснована тем, что принцип двойной записи отражает входящие и выходящие потоки только в положительном значении, поскольку в бухгалтерском учете отрицательные числа не используются. В нашей модели мы можем не разделять счета на активные и пассивные и описать математическую модель бухгалтерского счета в следующем виде:

S(t) =S(t- M) + U_in(t) - U_out(t), (3)

где: U_in – входящие средства за интервал ∆ t , U_out – выходящие средства за интервал ∆ t . Следует отметить, что в бухучете принято рассматривать заданные интервалы времени, связанные с отчетностью, например, месяц, квартал, год. Однако выражения (1) - (3) справедливы для любого момента времени t и любого интервала ∆ t . В рамках данной работы в дальнейшем примем, что ∆ t – некоторый заданный постоянный интервал времени, имеющий смысл шага дискретности модели, а время t – дискретное, принимает заданные значения с шагом ∆t, начиная с t = t₀ .

ДИСКРЕТНАЯ МОДЕЛЬ ПРОЦЕССА СНАБЖЕНИЯ

Рассмотрим процесс снабжения производственного предприятия (рис. 1).

На этой схеме показано, что деньги U₁ с рас-

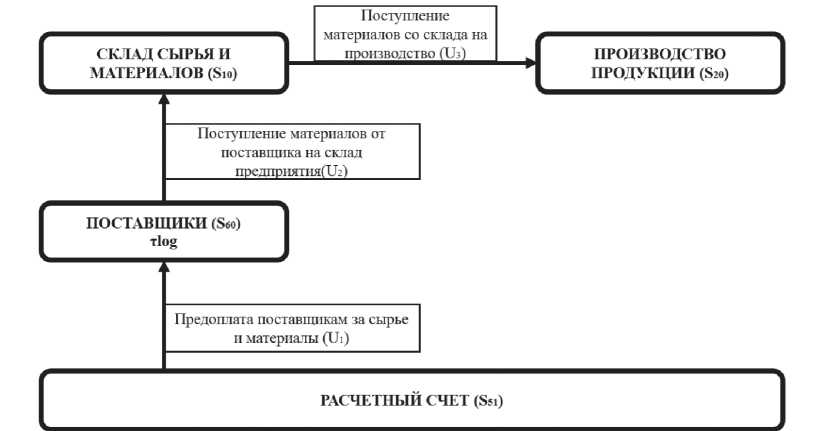
Рис. 1. Процесс снабжения производственного предприятия.

четного счета S₅₁ поступают к поставщикам S₆₀ на оплату сырья и материалов. Через определенное время τ _log материалы U₂ поступают на склад S₁₀ . Затем, по мере необходимости, материалы U₃ отпускают в производство S₂₀ .

Математическая модель склада описывается уравнением вида (3), где:

S(t) – количество сырья на складе в момент времени t ;

S(t – Δ t) – количество сырья на складе в момент времени t – Δ t ;

U_in(t) – приход сырья и материалов на склад за Δ t ;

U_out(t) – расход сырья и материалов со склада за Δ t ;

Таким образом, уравнение склада запишется в следующем виде:

МО = Mt - д0 + ^2(о - МО. (4)

Предположим, что задана программа выпуска продукции X_prog(t) для всех рассматриваемых t , начиная с t = t₀ , т.е. количество выпускаемой продукции за каждый интервал времени ∆ t , начинающийся в момент t – ∆ t . Тогда потребности необходимое количество материалов, труда и оборудования для производства продукции за интервал ∆ t , соответствующий дискретному моменту t , определяются выражением (5), представляющим собой вектор с пропорциональными компонентами [1, 2]:

ГЦ^) “ KyXp_rOg(t)

J V^t) = K^g^ ,       (5)

к^(0 ^— KfXp_TOg(t^

где: X_prog(t) – заданная программа выпуска готовой продукции,

• V_v(t) – необходимый объем материалов для производства X_prog(t) продукции,

• V_l(t) – необходимый фонд рабочего времени для производства X_prog(t) продукции,

V_f (t) – необходимый фонд станочного времени для производства X_prog(t) продукции,

K_v (t) – коэффициент материалоемкости единицы готовой продукции,

K_l (t) – коэффициент трудоемкости единицы готовой продукции,

K_f (t) – коэффициент фондоемкости единицы готовой продукции.

Таким образом, X_prog(t) , в соответствии с выражением (5), определяет требуемое количество ресурсов поступающих в производство.

Рассмотрим расход сырья и материалов со склада на производство. В случае, если материалов на складе достаточно для производства X_prog(t) , со склада берется необходимое количество материалов V_v (t) . В противном случае, если в наличии на складе материалов меньше чем необходимо для производства X_prog(t) , берется все имеющееся в наличии количество материалов, т.е. S₁₀(t) , и производится продукции столько, сколько позволяют эти материальные запасы.

Таким образом, расход материалов за интервал ∆ t описывается следующим выражением:

U₃(t) = min(v_v(t); 5₁₀(0).     (6)

Обычно поставщикам требуется некоторое время для доставки сырья и материалов на предприятие, следовательно возникает задержка между моментом заказа сырья и материалов и их поступлением на склад. Обычно работа с поставщиками ведется по предоплате, поэтому предполагаемся что задержка учитывается с момента оплаты партии товара. Отсюда, поток U₂(t) поступлений на склад описывается следующим выражением:

U₂(t) = и_г^-т_1од\         (7)

где: U₂(t) – количество сырья и материалов поступающих на склад за интервал ∆ t к моменту времени t ,

U₁(t – τ _log ) – количество денежных средств поступивших за интервал ∆ t на счет поставщиков τ _log времени назад,

τ _log – задержка по времени поставок материалов на склад.

Поскольку количество сырья и материалов зависит от количества денежных средств, имеющихся в распоряжении у предприятия, поток денежных средств поставщикам либо равен требуемому количеству сырья, то есть удовлетворяет требованиям производства при достаточном количестве денег, либо, если денежных средств не достаточно, мы закупаем столько сырья, на сколько это позволяет нам финансовое положение. Это можно описать уравнением следующего вида:

, (8)

где: U₁(t) – исходящие денежные средства,

V_v (t + τ _log ) – требуемое количество денежных средств для закупки сырья и материалов,

S₅₁(t) – имеющиеся в распоряжении денежные средства.

ИЛЛЮСТРАТИВНЫЙ ПРИМЕР

Рассмотрим пример производства профна-стила. На нашем производстве установлен план, по которому планируется выпуск продукции по 400 пог.м. в день. На нашем складе имеется запас сырья и материалов достаточный для производства 1600 пог.м. На расчетном счете лежит сумма денег, достаточная для закупки материалов на 10000 пог.м. Задержка τ _log принимается равной пяти дням, предполагая что мы работаем с одним и тем же поставщиком, с их средним периодом поставки материалов. Расчеты предоставлены в табл. 1.

На рис. 2. отображен реальный выпуск про- дукции (сплошная линия), относительно запланированного (пунктирная линия). Как видим из графика, в течении первых шести дней наше производство справляется с планом, но после начинается дефицит ресурсов.

Более подробное движение сырья и материалов через склад отражено на рис.3. в виде гистограммы.

На пятый день производства, как видно в табл. 1, мы оплатили поставку ресурсов на 3000 пог.м., но они, с учетом задержки, пришли только на девятый день. На графике это видно по прямой сплошной линии, означающая простой на предприятии.

Чтобы догнать производственный план, мы заблаговременно заказывали материалы, а выпуск продукции подняли, что видно в табл.1. в столбце «заданная программа».

На тринадцатый день мы сравнялись с производственным планом, но не снизили темп выпуска, что отражено на графике подъемом сплошной линии над пунктирной. Но увеличенный выпуск продукции увеличил количество потребляемых ресурсов, и поставки которые заказывали заранее не соответствовали производственным потребностям, из-за чего начались простои на предприятии и общий выпуск продукции начал снижаться до требуемого.

На семнадцатый была произведена последняя закупка сырья на 3000 пог.м., после чего деньги на нашем расчетном счете закончились. На двадцать второй день, на склад поступила последняя поставка и наших ресурсов хватало на производство продукции чуть выше запланированного уровня. На графике это видно, как линии идут параллельно друг к другу. Но на двадцать девятый день, наши ресурсы закончились, и производство

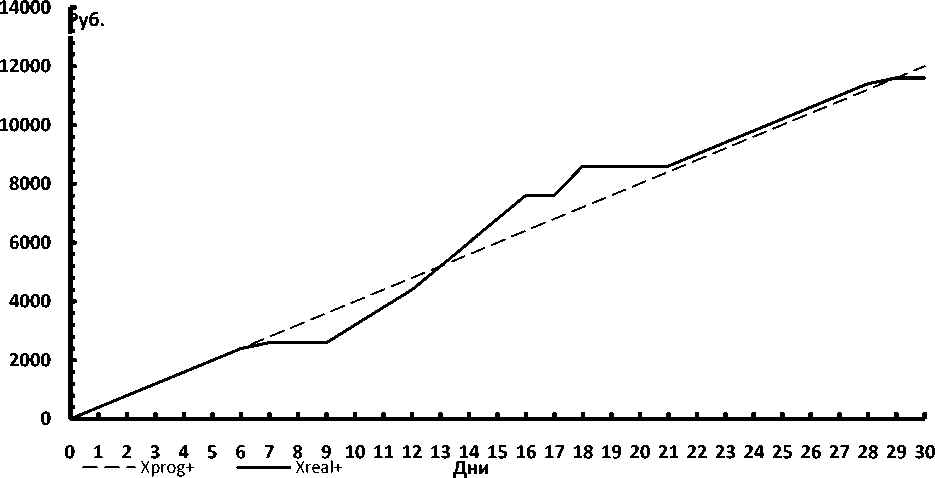
Рис. 2. Производственная программа

Таблица 1. Результаты расчета

К и	S о к к 05 ^ К ьо о а X	05 к S ЬЮ о 2 с а X	i к Л 05 m а о а с	К о си с О о « н	S о к ей	S о к 5	S о к сч'	S о к о ио	S о к NO	S о к о> X	S о к + о> X
0	0	0	0	0	10000	1000	0	1600	0	0	0
1	400	400	400	400	9000	0	0	1200	400	400	400
2	400	800	400	800	9000	0	0	800	400	400	800
3	400	1200	400	1200	9000	0	0	400	400	400	1200
4	400	1600	400	1600	9000	0	0	0	400	400	1600
5	400	2000	400	2000	9000	3000	1000	600	400	400	2000
6	400	2400	400	2400	6000	1000	0	200	400	400	2400
7	400	2800	600	3000	5000	1000	0	0	200	200	2600
8	400	3200	600	3600	4000	0	0	0	0	0	2600
9	400	3600	600	4200	4000	0	0	0	0	0	2600
10	400	4000	600	4800	4000	0	3000	2400	600	600	3200
11	400	4400	600	5400	4000	0	1000	2800	600	600	3800
12	400	4800	600	6000	4000	0	1000	3200	600	600	4400
13	400	5200	800	6800	4000	1000	0	2400	800	800	5200
14	400	5600	800	7600	3000	0	0	1600	800	800	6000
15	400	6000	800	8400	3000	0	0	800	800	800	6800
16	400	6400	800	9200	3000	0	0	0	800	800	7600
17	400	6800	800	10000	3000	3000	0	0	0	0	7600
18	400	7200	1000	11000	0	0	1000	0	1000	1000	8600
19	400	7600	1000	12000	0	0	0	0	0	0	8600
20	400	8000	1000	13000	0	0	0	0	0	0	8600
21	400	8400	400	13400	0	0	0	0	0	0	8600
22	400	8800	400	13800	0	0	3000	2600	400	400	9000
23	400	9200	400	14200	0	0	0	2200	400	400	9400
24	400	9600	400	14600	0	0	0	1800	400	400	9800
25	400	10000	400	15000	0	0	0	1400	400	400	10200
26	400	10400	400	15400	0	0	0	1000	400	400	10600
27	400	10800	400	15800	0	0	0	600	400	400	11000
28	400	11200	400	16200	0	0	0	200	400	400	11400
29	400	11600	400	16600	0	0	0	0	200	200	11600
30	400	12000	400	17000	0	0	0	0	0	0	11600

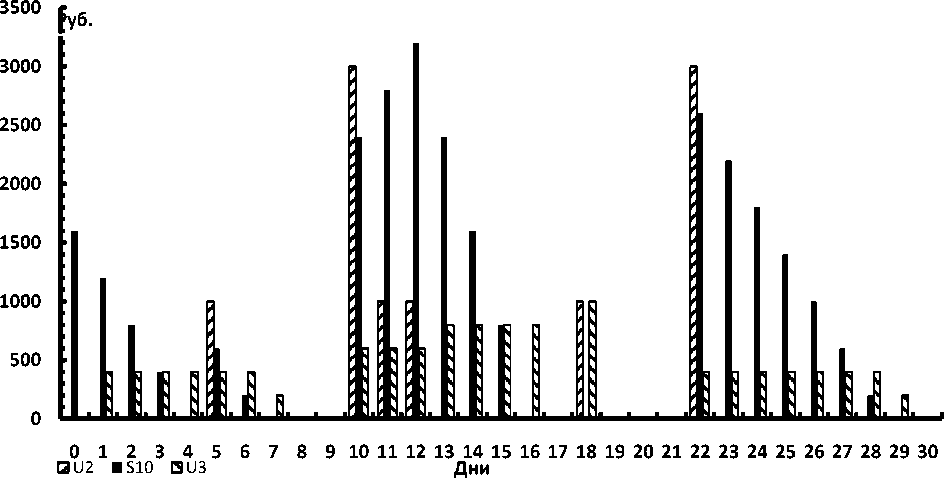
Рис. 3. Движение сырья и материалов через склад

встало, в следствии чего производственный план не был выполнен на запланированном уровне.

ЗАКЛЮЧЕНИЕ

В данной статье представлена математическая модель, отражающая процесс снабжения производственного предприятия на основе регистров бухгалтерского учета. Представленная математическая модель позволяет строить прогнозные траектории процесса снабжения и решать ряд типовых задачи на предприятии, таких как:

• -    планирование и прогнозирование производственной программы,

• -    прогнозирование поставок ресурсов,

• -    прогнозирование потребления ресурсов,

• -    решение задач логистики,

• -    ряд других задач.

Модель приводится в дискретном виде, однако может быть записана и в непрерывном виде. В этом случае она представляет собой систему дифференциальных и алгебраических уравнений с изменяющейся структурой. Опора на регистры бухгалтерского учета упрощает проблему идентификации модели и позволяет легко интерпретировать результаты.

Представленная модель может быть встроена как составляющая в общую математическую модель функционирования и развития предприятия.