Математическое моделирование процесса стратифицированного течения расплавов полимеров в осесимметричной постановке

На сегодняшний день продолжают оставаться востребованными исследования, посвященные изучению процессов многокомпонентных стратифицированных течений, сопровождающих и определяющих условия многих технологических процессов. Особое внимание следует уделить многослойным течениям жидкостей с аномально-вязкими свойствами, так как для подобных материалов режим течения будет определяться значительным числом влияющих факторов. Осложняет задачу взаимодействие нескольких потоков материалов с различными физико-реологическими свойствами. При этом имеются участки совместного течения: исследования показывают [1], что стабильность границы раздела оказывает существенное влияние на результат всего процесса и качество получаемого изделия. Этот процесс весьма затруднителен для непосредственного наблюдения, так как происходит внутри инструмента. Проследить распределение материалов можно, например, посредством моментального охлаждения инструмента с последующим разбором и произведением продольного среза. Далее с помощью специальных приемов можно получить картину распределения отдельных потоков [2–6]. Однако такой путь весьма трудоемок и подходит к каналам простой формы. Поэтому для анализа процессов течения полимеров в каналах сложной формы было принято решение о численном моделировании [7].

Рассмотренное в данной статье стратифицированное течение является частью процесса экструзионного наложения полимерной многослойной изоляции, в значительной степени определяющее качественные и эксплуатационные характеристики готовой кабельной продукции.

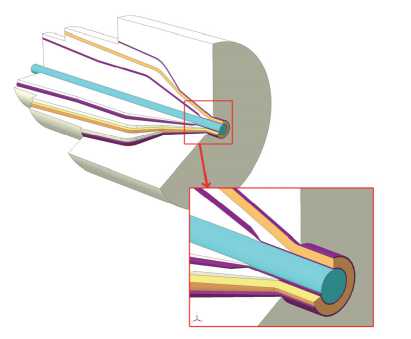
Рис. 1. Конфигурация кабельной головки

Геометрия каналов кабельной головки представлена на рис. 1. Различными цветами обозначены расплавы полимеров с отличающимися физико-реологическими свойствами. Высота канала на выходе составляет 6,9 мм, длина горизонтального участка соприкосновения с подвижной стенкой (жилой) 27 мм, толщина канала 1 в зоне примыкания к подвижной жиле 0,7 мм.

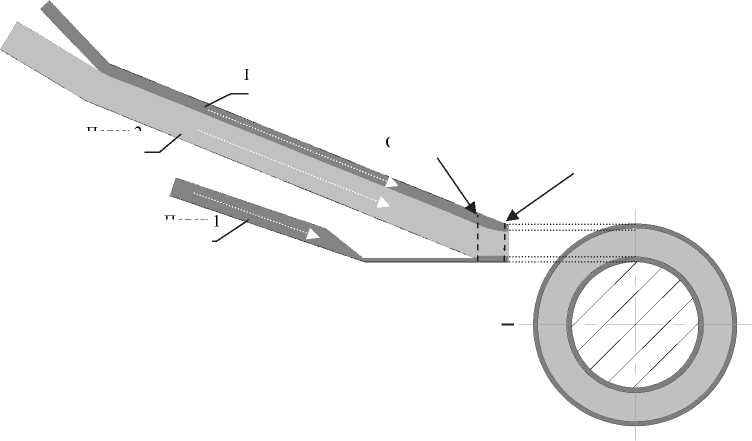
Такую геометрию удобно рассматривать в цилиндрической системе координат (рис. 2).

Здесь различными цветами отмечены слои материалов с различными свойствами, при этом хорошо заметны участки совместного течения. Было получено расположение границ раздела потоков на выходе каналов, по которым можно судить о количестве материала, накладываемого на готовое кабельное изделие. Кроме того, в ходе решения задачи строились тепловые поля, по которым отслеживались локальные перегревы. Такие превышения температуры обусловлены внутренними диссипативными источниками тепла, возникающими в результате трения слоев расплава друг о друга. Это вызывает дополнительный разогрев полимера, что негативно сказывается на его эксплуатационных свойствах.

Поток 3

Сечение А

Сечение Б

Поток 2

r▲

Поток 1

Подвижная стенка

ζ

Ось симметрии

Рис. 2. Каналы истечения полимеров в цилиндрической системе координат

Математическое описание процессов тепломассообмена расплавов полимера при стратифицированном течении основано на законах сохранения [8].

Для упрощения задачи был сделан ряд допущений:

• –    процесс стационарный;

• –    среда несжимаемая, без упругих свойств [9];

• –    массовые силы значительно меньше поверхностных;

• –    течение осесимметричное;

• –    на границах канала реализуются условия прилипания и непроницаемости;

• –    теплофизические характеристики постоянны.

С учетом допущений система дифференциальных уравнений [8, 10] для каждого из слоев потока в скоростях имеет следующий вид:

1 Э^ +5 V ; = 0, r д , д;

д (2|1* J+2ц Эд v, д r к э д r J r д r

-

2 . д Г / д v, —Ц э V r ⁺Ч7 Ц э

∂

ζ ∂ v

∂ P

r

∂ζ

д r dZ J d r ’

Г д V;

д   , Г д V, дv

Ц э       ' "47

∂ r

∂ v

к

∂ r ∂ζ

J_

д V _Z A

Ц Э Г ^v

⁺ r к д r a; Jа; ^{2 Цэ} -

∂

к

∂ζ

Г д T    д T

ρiCi v    +v кr дr   ;д;

∂ P

д;,

J

к

1 д( „TЛ д r X     +X i+ Ф, r ar к    дr J д; ,

i ∂ T

к

∂ζ

J

где индекс i определяет номер слоя в потоке и соответствующий ему материал; r , Z - радиальная и продольная цилиндрические координаты; v r , v z - компоненты вектора скорости; Ф - диссипативный источник тепла; P - давление; T - температура; р - плотность; C - теплоемкость; X - теплопроводность; и , - эффективная вязкость, являющаяся функцией скорости сдвига и температуры [11]:

n - 1

у J ,                    (5)

где ц о - начальная вязкость при Т ) ; в - температурный коэффициент вязкости; n - коэффициент аномалии вязкости; 1 ₂ - второй инвариант тензора скоростей деформации.

Система дифференциальных уравнений (1)-(5) замыкалась следующими граничными условиями:

• -    на неподвижных стенках компоненты скорости равны нулю;

• -    на границе контакта с подвижной жилой продольная компонента скорости равна скорости движения жилы (0,183м/с);

• -    на входе в каналы задавались давления;

• -    на выходе - ГУ второго рода по скорости и температуре;

• -    температура неподвижных стенок каналов 443 К;

• -    температура расплавов полимеров на выходе из экструдеров 423 К;

• -    температура подвижной жилы 383 К.

На границах раздела потоков задавались следующие граничные условия [12]:

по напряжениям

( т rr cos( r , n ) + т r z cos( z , n )) 1 1 = (t rr cos( r , n ) +т r z cos( z , n )) I 2 , (t r z cos( r , n ) + T zz cos( Z , n )) I 1 = (t r z cos( r , n ) + T zz cos( Z , n )) I 2 , (t rr cos( r , n ) + т r z cos( z , n )) I 2 = (t rr cos( r , n ) + т r z cos( z , n )) I 3 , (t r z cos( r , n ) + T zz cos( z , n )) I 2 = (t r z cos( r , n ) + T zz cos( z , n )) I 3 ,

по скоростям vr I2 = vr I3;

v z 1 1 = v z | 2 , v z | 2 = v z | 3 ,

по потокам тепла qr 11=qr I2; qzk=qz |2, qr 12=qr 1з; qz I2=qz 1з,

по температуре на границах раздела потоков

T I 1 = T I 2 ;      T I 2 = T I 3 ,                             (9)

где индексы 1, 2, 3 – номера потоков стратифицированного течения (см. рис. 2); т _rr T _r z - нормальные и касательные напряжения, определяемые как

T r = 2 а э ^d v , о r

^т r z =a э

^Л d v_r д v z ^Л I dz + д r )

где q r , q ζ – потоки тепла в направлении соответствующих осей.

Сформулированная таким образом система дифференциальных уравнений (1)–(4), дополненная реологическими уравнениями состояния (5), граничными условиями (6)–(10) и свойствами перерабатываемых материалов (таблица) решалась численно, с применением метода конечных элементов в программном комплексе Ansys.

Для оценки стабильности решения было проведено два расчета: один в режиме заданного расхода, другой – в режиме заданного перепада давления в каналах.

Для сравнения модели с заданными расходами (назовем ее «модель Q») с результатами, полученными для модели с заданными перепадами давления (назовем ее «модель P»), были рассчитаны поля тем- ператур, скоростей, распределения потоков, а также построены эпюры скорости по некоторым поперечным сечениям каналов (рис. 3).

Физико-реологические свойства исследуемых материалов

Материал	Начальная вязкость μ 0 при Т = 433K, Па ⋅ с	Температурный коэффициент вязкости β, 1/K	Показатель аномалии вязкости n	Плотность ρ, кг/м3	Коэффициент теплопроводности λ, Вт/(м·К)	Удельная теплоемкость C , Дж/(кг·К)
Изоляция (слой 2)	14946	0,0168	0,542	779	0,182	2500
Экран (слои 1, 3)	38523	0,0027	0,251	1080	0,182	2500

Для модели P на входах в каналы задавались давления в узлах в виде прямоугольных эпюр.

Расход в модели Q задавался через узловые скорости для каждого из трех входов, вектор скорости ориентирован по нормали к линии, ограничивающей вход каждого канала. Эпюры скорости имели прямоугольный вид.

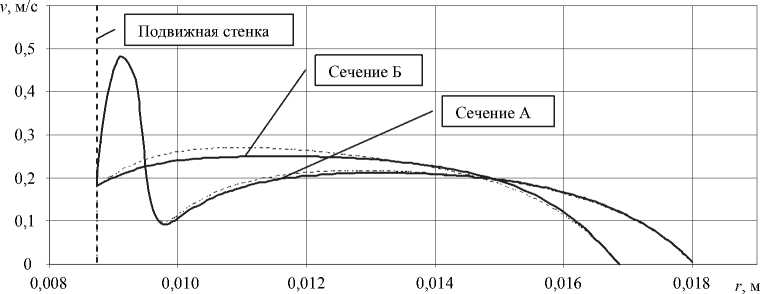
Рис. 3. Сравнение эпюр скоростей для различных сечений и моделей:     – «модель

Q »;     – «модель P »; сечение А и сечение Б обозначены на рис. 2

Анализ эпюр скорости показал максимальное отклонение результата модели P от модели Q в сечении Б (т.е. ближе к выходу из расчетной области) 8,4 % (при этом среднее отклонение скорости в этом сечении не превышает 3,9 %). Для сечения А максимальное отклонение скорости составило 2,3 %, среднее – 0,9 %.

Расхождение между моделями Q и P при приближении к выходу из канала связано с изначальным заданием давления на границах в виде прямоугольных эпюр (в исходной модели P распределения давлений на входах в каналы и на выходе из него носили сложный нелинейный характер). Поэтому картина потоков в непосредственной близости от этих границ несколько искажалась.

Эпюра скорости расплава полимера в узком канале, образованном головкой и подвижной жилой, в поперечном сечении имеет явно выпуклый характер (скорость по центру этого канала более чем в 2,5 раза превышает скорость движения жилы), что объясняется малым поперечным сечением кольцевого канала и высоким перепадом давления. По мере слияния потока 1 и совместного потока 2 и 3 на расстоянии между сечением А и сечением Б происходит смещение границы раздела этих потоков в направлении от жилы, тем самым поперечное сечение кольцевого канала увеличивается, скорости потока 1 выравниваются и приближаются к скорости движения жилы (см. рис. 2).

Поскольку численная реализация предложенной математической модели стратифицированного течения подразумевает соответствующую итерационную процедуру, необходимо определить некоторое условие ее окончания. Так как одним из основных контролируемых параметров являлись толщины слоев изоляционных материалов на выходе из канала, была проведена серия расчетов, целью которой стало определение характера зависимости толщин слоев от количества счетных итераций. Результатом этой серии расчетов явился график, представленный на рис. 4.

Анализ полученных кривых показал, что для стабилизации решения достаточно 1500–2000 счетных итераций. Дальнейшее увеличение количества итераций на характер распределения потоков материала в установившемся стратифицированном течении практического влияния не оказывало. Следовательно, в расчетах при той же геометрии модели и той же сетке разбиения на конечные элементы можно ограничиться установленным количеством итераций.

Для определения достаточного количества конечных элементов были проведены исследования, заключающиеся в анализе распределения потоков и координат границ раздела потоков для различных сеток. При этом в рамках одной сетки все конечные элементы были одного размера, преимущественно использовались четырехузловые элементы.

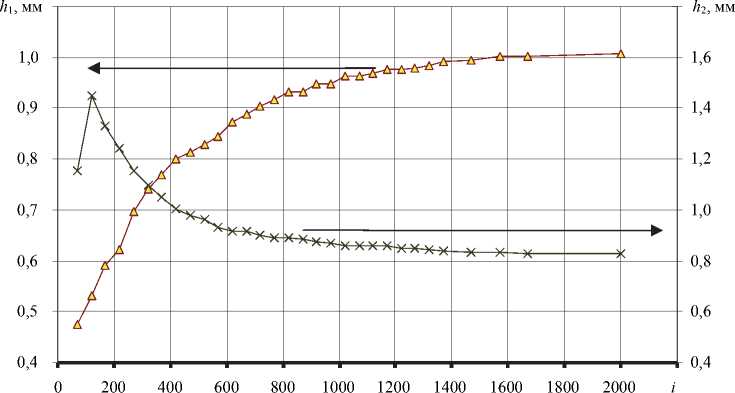
Рис. 4. Изменение толщин слоев материала при увеличении количества счетных итераций (i):    – внешний экран по изоляции (h1); – внутренний экран по жиле (h2)

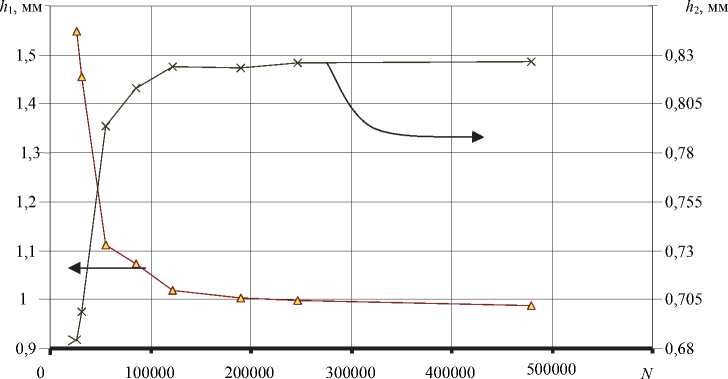
Рис. 5. Изменение толщин слоев материала при увеличении количества элементов ( N ):    – внешний экран по изоляции ( h 1 );    – внутренний экран по жиле ( h 2 )

Из рис. 5 видно, что при увеличении количества конечных элементов от двухсот тысяч и выше характер распределения потоков не менялся, на что указывала стабилизация границ раздела потоков разнородных материалов на выходе расчетной области.

Для проверки предположения о возможных погрешностях расчета, связанных с разбиением на конечные элементы, сетка частилась, прежде всего в зоне слияния потоков 1 и 2 (см. рис. 2), так как это наиболее сложный с точки зрения происходящих процессов участок. Поскольку увеличение числа конечных элементов не приводило к существенному изменению результатов (в том числе и эпюр скорости в различных сечениях) был сделан вывод о достаточной точности счета.

Изначально рассматривалась геометрия реально существующей кабельной головки для наложения трехслойной изоляции, эксперименты с которой привели к получению продукта с неудовлетворительным качеством. Измерение полупроводящего слоя по жиле показало недостаточную его толщину и неравномерный характер наложения. Предварительный анализ ситуации с использованием предлагаемой математической модели и численного метода выявил причину [13]. В части канала, в которой поток материала, образующий слой полупроводящего экрана по жиле, перетекает из коническо-цилиндрического зазора с неподвижными стенками в кольцевой зазор, где одна из стенок образована подвижной жилой, возникало вихревое течение, которое оказывало существенное влияние на условия протекания материала через поперечное сечение канала (рис. 6).

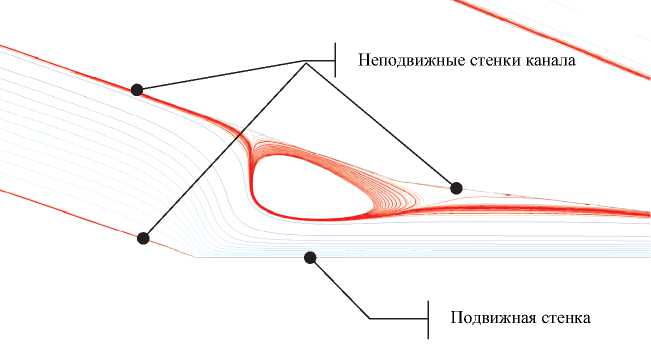
Рис. 6. Завихрение потока в канале исходной кабельной головки

Подобное явление достаточно хорошо известно и описано, например, в [14], где автор отмечает влияние такого вихревого течения на качество получаемого изделия.

Таким образом, при исследовании существующего технологического режима возникла новая задача, заключающаяся в рационализации геометрии кабельной головки для заданного технологического режима. В результате была предложена новая альтернативная геометрия кабельной головки для одновременного наложения нескольких слоев изолирующего материала, которая во всем технологическом диапазоне параметров экструзии показала отсутствие ранее указанного явления завихрения материала (рис. 7).

Неподвижные стенки кан

"I Подвижная стенка

Рис. 7. Отсутствие завихрений материала в канале предложенной геометрии

Так, после предварительного анализа существующей кабельной головки были определены недостатки ее геометрии и предложена новая конструкция канала истечения полимера, формирующая более рациональные потоки материала.

На рис. 8 приведен фрагмент каналов кабельной головки, на котором характеристически представлено отличие исходной кабельной головки от предложенного варианта.

Штриховой линией показано предложенное утонение канала, препятствующее возникновению завихрения.

С целью определения степени влияния температурной зависимости вязкости на возникновение завихрения материала были проведены исследования, подробно описанные в [15]. В целом они показали, что эффект завихрения обусловлен именно наличием сложной модели вязкости, учитывающей, помимо всего прочего, и температуру материала. В модели, где вязкость зависела исключительно от скорости сдвига, подобного завихрения не образовывалось.

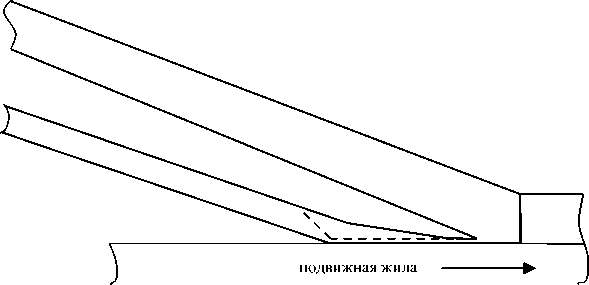
Рис. 8. Различия в геометрии каналов исходной и предложенной кабельной головки

Предложенная геометрия кабельной головки была численно исследована на возможность переработки материалов, физико-реологические свойства которых отличаются от представленных в данной работе (плотности в диапазоне 400–1400 кг/м³, n = 0,1…0,7, µ 0 = = 2000…80000). Результаты позволяют сделать вывод о возможности такой переработки без изменения предложенной конструкции. Однако для определения возможности переработки материалов, свойства которых существенно отличаются от приведенных, или описываются иными законами, или моделями (например, ПВХ), требуются дополнительные исследования.

Полученное в ходе численного моделирования решение позволило построить совокупность температурных полей, распределений потоков полимеров в каналах, поля давления, скорости. Возможность построения границы раздела потоков позволила судить о толщине накладываемых на жилу слоев на выходе из кабельной головки, а полученные распределения температуры – контролировать внутренние перегревы в слоях расплава полимера.

На рис. 9 представлено поле давления внутри кабельного канала. Видно, что наибольшее давление создается в канале, по которому истекал полимер, образующий внутренний полупроводящий слой по жиле. Это связано с наименьшим поперечным сечением данного канала и с достаточно высокой вязкостью полимера.

Рис. 9. Поле давлений в каналах кабельной головки

На рис. 10 приведено поле скоростей движения расплава по каналам кабельной головки. Наибольшая скорость потока наблюдалась в самом узком сечении канала (сужение при перетекании материала из канала с неподвижными стенками в канал, одна из стенок которого образована подвижной жилой). При этом максимальная скорость в этом суженом участке примерно в 2 раза превосходила скорость движения жилы.

Contours of Velocity Magnitude (m/s)

Рис. 10. Поле скоростей в каналах кабельной головки

Анализ температурного поля, приведенного на рис. 11, показал достаточно равномерный характер прогрева материала в канале. При этом на выходе полимер практически сохранял температуру расплава, получаемого от экструдера (рис. 12), – 423 К, а средняя температура на выходе 426 К. На неподвижных стенках температура соответствовала температуре подогрева кабельной головки, что улучшало прохождение материала через сечение канала.

Contours of Static Temperature (k)

Рис. 11. Поле температур в каналах кабельной головки

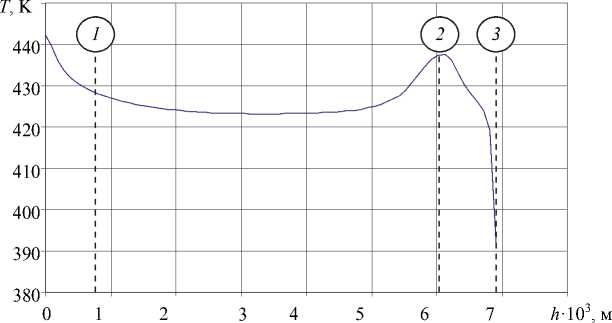
Рис. 12. Распределение температуры в сечении Б ( h – высота канала): 1 – граница полупроводящего экрана по изоляции; 2 – граница полупроводящего экрана по жиле; 3 – токопроводящая жила

Рис. 11–12 показывают невозможность оперативного контроля вероятных диссипативных перегревов полимера в кабельной головке при помощи измерительных инструментов на выходе из головки, так как температуры выравнивались и уловить перегрев не представлялось возможным. Таким образом, предлагаемый способ контроля внутренних перегревов на основе численного моделирования представляется одной из возможных альтернатив контроля качества изоляции на предмет наличия следов термической деструкции материала.

Рис. 13. Распределение потоков материала внутри каналов кабельной головки

Рис. 13 демонстрирует траектории движения расплава полимеров по коническо-цилиндрическим каналам кабельной головки и отражает взаимодействие потоков при их слиянии. На рис. 14–15 отдельно показаны границы потоков расплавов полимеров. Можно отметить стабильность границ на всем участке взаимодействия потоков, что обеспечивает хорошее качество получаемой многослойной изоляции.

Границы потоков, изображенные на рис. 15, позволили определить толщины накладываемых на жилу полимерных полупроводящих и изолирующих слоев.

Рис. 15. Границы раздела потоков на выходе из кабельной головки

Для оценки степени влияния различных факторов на исследуемый процесс формования многослойной полимерной изоляции были проведены численные эксперименты, результатами которых явились графические зависимости толщин накладываемых изоляционных слоев от массового расхода и линейной скорости движения жилы.

Графики, приведенные на рис. 16, показывают изменение толщины накладываемых слоев материала при изменении массового расхода в первом ( Q 1 ), втором ( Q 2 ) и третьем ( Q 3 ) каналах. При увеличении расхода Q 1 в 10 раз толщина экрана по жиле возрастала в 6,8 раз, толщина изоляции уменьшалась на 20 %, а толщина экрана по изоляции уменьшалась на 30 %. При увеличении расхода Q 2 в 8 раз толщина экрана по жиле уменьшается в 2 раза, толщина изоляции возрастает в 3,7 раза, а толщина экрана по изоляции падает в 5,7 раза. При увеличении расхода Q 3 в 10 раз толщина экрана по жиле падает на 20 %, толщина изоляционного слоя падает на 40 %, а толщина экрана по изоляции возрастает в 5 раз. Анализ графиков позволил сделать вывод о минимальном влиянии расхода первого канала на два других.

На рис. 17 показана зависимость толщин слоев от линейной скорости. При увеличении V л в технологическом диапазоне в 8 раз толщина экрана по жиле уменьшалась в 3,5 раза, толщина изоляции и толщина экрана по изоляции возрастали соответственно на 12 и 28 %.

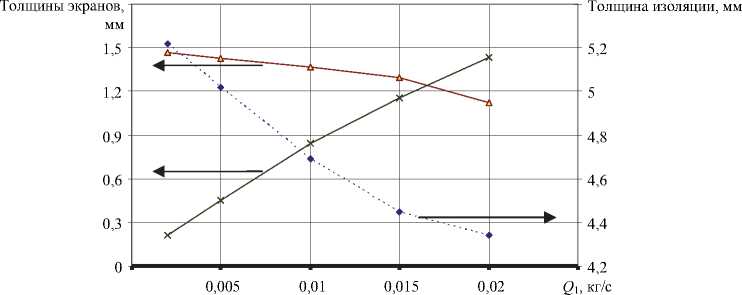
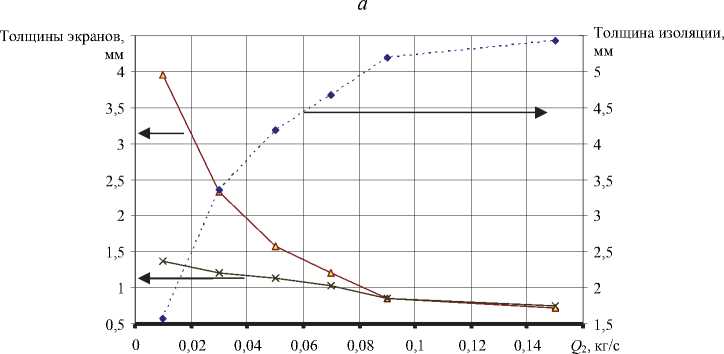
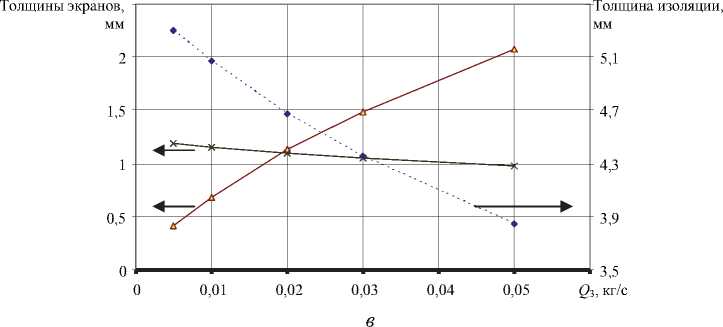
Рис. 16. Изменение толщин слоев материала при изменении расхода: а – в канале 1;

б – в канале 2; в – в канале 3;      экран по изоляции; -------изоляция; —X  экран по жиле

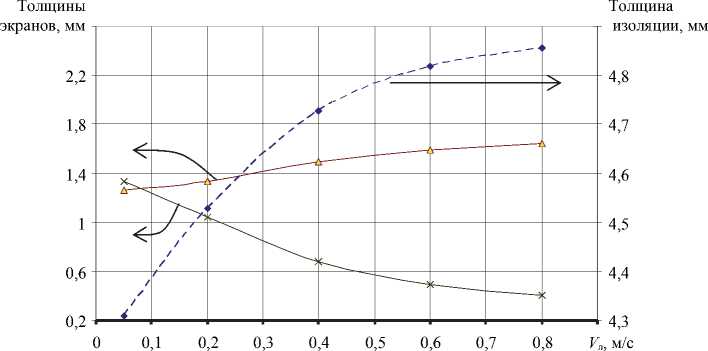
Рис. 17. Изменение толщин слоев материала при изменении линейной скорости V л : экран по изоляции; - - - ♦- - - изоляция; —X экран по жиле

Толщины слоев контролировались на выходе кабельной головки. Таким образом, суммарная толщина всех слоев фиксирована и ограничена высотой канала на выходе. При увеличении линейной скорости эпюра скорости материала на выходе теряла выпуклый характер: материал увлекался подвижной стенкой (жилой), и характер эпюры смещался ближе к течению Куэтта. Скорости второго и третьего потоков уменьшались, следовательно, для сохранения требуемого расхода было необходимо увеличение ширины каждого из потоков.

Таким образом, в результате данного исследования была разработана осесимметричная модель трехслойного неизотермического течения расплавов полимера в системе коническо-циллиндрических зазоров кабельной головки. В ходе исследований была предложена альтернативная геометрия кабельной головки, оптимизирующая потоки расплавов полимеров и устраняющая явление противотока.

Произведена оценка степени влияния различных факторов на толщины накладываемых на готовое кабельное изделие слоев, в результате чего были построены зависимости геометрических свойств производимых кабельных изделий от расходов и линейных скоростей движения жилы. Эти зависимости позволяют оперативно менять технологические параметры экструзионной линии, заранее зная получаемый в итоге результат.

Результаты данного исследования с успехом могут быть применены при изучении процессов неизотермических многослойных течений в кабельных головках; при проектировании систем автоматизированного управления экструзионными линиями [16, 17].

Работа выполнена при финансовой поддержке РФФИ (грант №13-08-96034).