Математическое моделирование процесса сушки древесных отходов

влагоудаления из древесной щепы, являющейся отходами переработки древесины, следует заметить, что данный процесс имеет ряд отличий по сравнению с влагоудалением из массива древесины. За счёт повреждённой структуры материала интенсивность внутреннего влагопереноса в продольном и поперечном направлениях значительно отличается от аналогичных параметров у массива соответствующих пород. Без учёта этой особенности математические модели процесса сушки не будут обладать высокой точностью.

Ряд исследователей [1-4] разделяют «активные» и «пассивные» режимы сушки. Основными признаками активных гидродинамических режимов по мнению Сажина [2, 8, 9] являются: развитая поверхность взаимодействия фаз, гидродинамическая устойчивость (стабильность гидродинамической обстановки во времени по всему объему аппарата), приближение гидродинамической модели потоков в аппарате к модели идеального вытеснения, а также увеличение относительной скорости движения фаз. Повышение активности гидродинамической обстановки в сушильном аппарате связано с увеличением межфазных относительных скоростей, подвижности и столкновения частиц, а соответственно среднего коэффициента теплоотдачи, что интенсифицирует процесс, однако требует роста затрат. За косвенный показатель гидродинамической активности аппарата можно принять коэффициент межфазной теплоотдачи с учетом доли тепла, идущей на испарение влаги. Это так, если речь идёт об этапе сушки с постоянной скоростью влагоудаления.

Рассматривая процессы сушки, необходимо понимать, какие процессы протекают в материале при удалении влаги. При нарушении равномерного распределения влаги по объему материала, то есть при наличии градиента влажности влага перемещается из мест с большей концентрации влаги в места менее увлажненные. В процессе сушки происходит испарение влаги с поверхности материала, при этом влажность верхних слоёв уменьшается и за счёт разности концентраций между поверхностными и внутренними слоями возникает внутренняя диффузия. Но нагрев поверхности приводит к изменению направления движения влаги в материале [6]. Процесс удаления влаги нестационарен.

Необходимо выделить несколько этапов сушки. Традиционно выделяют период прогревания материала, при этом на поверхности материала достигается температура влажного термометра. В конце данного периода достигается максимальная скорость сушки.

Она определяется равенством скоростей диффузии влаги к поверхности и скорости испарения. Это характерно для всего второго этапа сушки, когда скорость испарения остаётся постоянной. В этот период удаляется влага намокания, удаляется влага из пор и крупных капилляров, происходит снижение уровня влагосодержания на 70-80%. На этом этапе процесс подчиняется законам испарения жидкости со свободной поверхности, без проникновения границы испарения под поверхность. При стабильных внешних условиях скорость сушки на отрезке постоянна. Когда количество влаги в поверхностном слое материала уменьшается и становится близким к сорбционной емкости, испарение влаги замедляется, так как скорость подачи ее к поверхности меньше, чем скорость испарения. Наступает третий этап сушки – испарение влаги с ненасыщенной поверхности. На этом этапе происходит испарение капиллярной влаги. После испарения всей влаги из макропор и для ряда материалов наступает этап стабилизации скорости сушки.

Наличие того или иного периода сушки обусловлено особенностями структуры и начальной влажностью материала. В коллоидных капиллярно-пористых телах влага может перемещаться в виде жидкости и в виде пара [5]. Основными факторами перемещения влаги в материале является градиент влажности и температуры. Влага находятся в равновесном состоянии в материале при условии равенства температур в различных её точках и равномерном её распределении по всему объему материала. При нарушении равенства температур, то есть при наличии градиента температуры, влага перемещается от поверхности с высокой температурой к поверхности с более низкой температурой. При незначительном перепаде температур влага перемещается в виде жидкости, а при большом перепаде – в виде пара. Перемещение влаги по направлению потока тепла обычно называется термодиффузией [7, 9] . При нагревании поверхностное натяжение изменяется. На нагретой поверхности поверхностное натяжение и капиллярное давление уменьшаются, капиллярный потенциал нагретой поверхности уменьшается, и жидкость перемещается от мест более нагретых к местам менее нагретым. То есть на третьем этапе сушки существует механизм обратного переноса влаги от зоны испарения в подповерхностные слои. Поскольку на процессы прогрева и диффузии влаги взаимно связаны и обладают определённой инерционностью то интенсифицировать процесс удаления влаги можно интенсифицировать периодическим нагревом и охлаждением поверхности. При этом можно ожидать наличия оптимальной частоты смены нагрева и охлаждения зависящей от амплитуды температур, влажности материалов, теплоёмкости каркаса тела [5-7].

Рассмотрим наиболее часто применяемые математические модели расчёта тепловых полей и полей влажности материала. Лебедев П.Д. в «Теплообменные сушильные и холодильные установки» воспользовался следующими формулами к изучению процесса сушки.

ат csp0 cs at где - внутренний положительный источник тепла;

• - плотность сухого материала; с в – теплоемкость влажного материала; r - теплота парообразования; ε – коэффициент внутреннего испарения влаги; t – температура материал; a – коэффициент температуропроводности материала при его средней влажности.

У Лыкова при p=cons дифференциальное уравнение переноса тепла и массы во влажном теле имеет вид:

дсо

— = DyoV2a>+DYo6V2d

ОТ

doo - г доо

— = aV^ + г-■ — от            с от где r – удельная теплота испарения; δ – коэффициент термодиффузии, характеризует относительный мас-соперенос пара и жидкости; ε – критерий испарения, характеризующий долю переноса влаги в виде пара от общего ее потока, 0≤ε≤ 1, при ε= 0 перенос влаги происходит в виде жидкости, при ε =1 за счет диффузии пара.

Процесс сушки, Лыков А.В. разделил на два этапа и кривую скорости во втором этапе заменил прямой линией, геометрическое соотношение выглядит так:

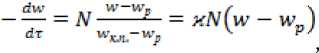
где N - постоянная скорость сушки в первом периоде;

-приведенная критическая влажность, которая может быть больше или меньше действительной критической влажности;                  - относитель ный коэффициент сушки, зависящий от характеристики материала и определяемый экспериментально.

После интеграции уравнение будет выглядеть следующим образом:

X = l/(w_K„. - W_p)

где -приведенная критическая влажность, которая может быть больше или меньше действительной критической влажности; w1 и w2 -начальная и конечная влажность сушимого материал; wр -равновесная влажность.

Учитывая, многообразие математических моделей процесса сушки приходится учитывать те ограничения, которые накладывает сам объект удаления влаги – щепа. Поскольку в этом случае толщина одиночного элемента древесной щепы много меньше других характерных размеров использование двумерных а тем более трёхмерных моделей вызывает сомнение, учитывая что конечная влажность не должна быть ниже 12-13%, учёт режима с входом границы испарения в массив тела, как минимум, требует проверки. Конечная влажность древесной щепы оценивается в 13,5%, что определяется технологией дальнейшей переработки.

Экспериментальная часть. В ходе расчетов авторами были приняты следующие допущения: предельная температура сушильного агента составляла 1400С (требования пожароопасности) при использова- ния воздуха в качестве сушильного агента, недопущение обугливания поверхностного слоя сушимого мате- риала, что отрицательно сказывается на дальнейшем технологическом процессе. Для решения поставленной задачи была применена система одномерных уравнений:

∂ u

∂ τ

∂2u∂

= D ⋅ ρ ⋅    + D ⋅ ρ ⋅ δ ⋅

∂x 2

∂ x

∂T    ∂2T     r∂

=α    +ε⋅⋅

∂τ    ∂x 2     c∂

Масса удаляемой влаги

∂u∂ m =-D⋅ρ⋅   -D ⋅δ⋅ ρ⋅

B          ∂x∂ где T – температура, u - влагосодержание, х – текущая координата α – температуропроводность, D – коэффи- циент диффузии, r – скрытая теплота парообразования, ε – критерий испарения ε=0 при диффузии влаги и ε=1 при диффузии пара, τ – время, δ – коэффициент термодиффузии с- теплоёмкость.

Одним из основных коэффициентов переноса массы влаги является D – коэффициент диффузии пара и жидкости, в некоторых случая его называют коэффициентом потенциалопроводности или влагопроводи-мости, зависит он от влажности и температуры вещества. При этом одной из важнейших задач является определение коэффициента диффузии (потенциало-проводности) и коэффициента термодиффузии. Последний также зависит от температуры и влажности вещества.

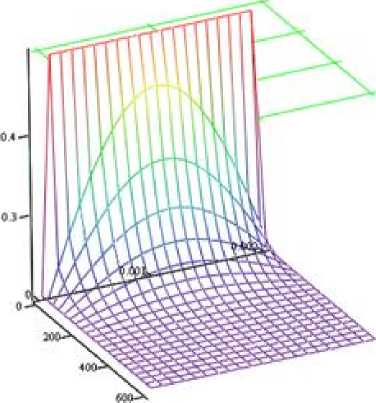
Рис. 1. Трёхмерное представление полученной зависимости изменения влагосодержания

Критическим участком математического моделирования процесса влагоудаления является определение коэффициента диффузии и термоградиентного коэффициента. На основании анализа собственных экспериментальных данных, а также анализа данных по значению коэффициента термодиффузии, приведенных в работах [5-7, 9] авторами была получена зависимость коэффициента термодиффузии:

δ = 0.241 ⋅ U - 0.048 ⋅ t - 1.412 ⋅ 10 ^-3 ⋅ U ⋅ t -

- 1.188 ⋅ 10 ^-3 ⋅ U ² + 5.086 ⋅ 10 ^-4 ⋅ t ²

где t – температура, u - влагосодержание.

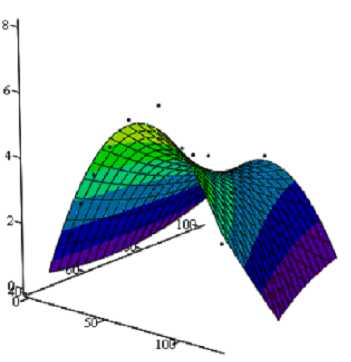
Рис. 2. Зависимость термоградиентного коэффициента от температуры и влагосодержания

Для анализа эффективности осциллирующего режима был поставлен ряд численных экспериментов с использованием модернизированной модели, основной задачей которого, являлось определение режима обеспечивающего одинаковое по сравнению со стационарным время влагоудаления при меньших энергетических затратах. Графики на рис. 3-6 доказывают одинаковое время влагоудаления по объёму с осциллирующим и не с осциллирующим режимах сушки, при этом при осциллирующим режиме потребление тепловой энергии на 20% меньше.

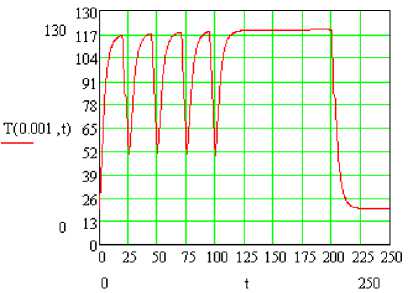
Рис. 3. Изменение температуры в центре исследуемого объекта при осциллирующем режиме подвода тепла

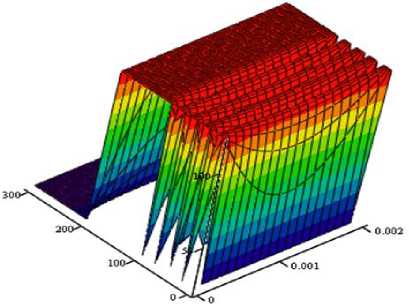
Рис. 4. Графики влагосодержания по сечению тела во времени

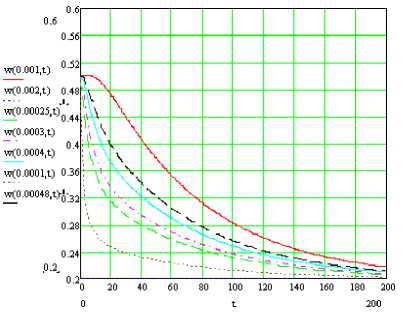
Рис. 5. Осциллирующий режим сушки

Выводы: авторами была разработана математическая модель удаления влаги из щепы с учётом зависимости термоградиентного коэффициента от влажности материала и температуры. Проведя математическую обработку экспериментальных данных методом наименьших квадратов авторами была получена регрессионная зависимость термоградиентного коэффициента от температуры и влажности, для сушки древесных отходов. Произведена оценка эффективности режимов осциллирующей сушки.

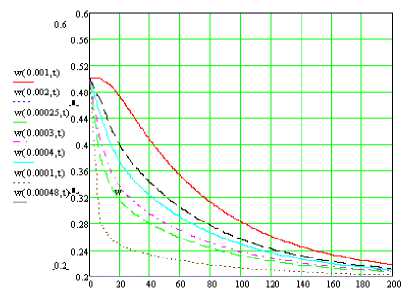
Рис. 6. Стационарный нагрев исследуемого объекта

• 2.

• 3.

• 4.

• 5.

• 6.

• 7.

• 8.

• 9.