Математическое моделирование процесса теплообмена в солнечном коллекторе с учетом времени релаксации тепловых напряжений

Актуальность

В России и во всем мире в последнее время уделяется большое внимание развитию использования альтернативных (возобновляемых) источников энергии. В нашей стране, в частности, был принят Федеральный закон «Об энергосбережении и о повышении энергетической эффективности и о внесении изменений в отдельные законодательные акты Российской Федерации» № 261-ФЗ от 21.11.2009 г.

В связи с этим возрастает значение использования альтернативных источников энергии. Исследованию различных проблем, связанных с использованием возобновляемых источников энергии, в том числе математическому моделированию в области возобновляемых источников энергии, посвящено много работ [1, 2, 4, 5 и др.].

Солнечные коллекторы — это самое первое открытие человеком возможности использования возобновляемой энергии солнца для своих нужд. В настоящее время использование солнечных коллекторов также широко распространено. Интерес представляет математическое моделирование процессов теплообмена в солнечном коллекторе для повышения эффективности его работы и для возможности управления солнечным коллектором.

Постановка задачи

Солнечные коллекторы делятся на два основных типа — плоские солнечные коллекторы и трубчатые (вакуумные). Наибольшее распространение имеют плоские коллекторы, это определяется их дешевизной, простотой использования.

Стандартный деревянный стеклопакет, установленный в большинстве квартир, построенных до 90-х гг., представляет собой также солнечный коллектор. У пластиковых стеклопакетов возможности поглощения и накопления тепла выражены слабее, так как нет той самой весьма полезной с точки зрения поглощения тепла широкой прослойки воздуха между внутренними и внешними рамами.

Можно использовать набор из двух пластиковых стеклопакетов и реализовать прослойку воздуха между ними, таким образом добиться эффекта солнечного коллектора.

С практической и научной точки зрения представляет интерес решение проблемы учета инерции теплопередачи при наличии воздушной прослойки. В частности, представляет интерес оценка влияния теплопотерь через оконные конструкции с учетом застекленной лоджии.

В случае наличия застекленной лоджии даже при использовании пластиковых стеклопакетов образуется воздушное пространство между оконными конструкциями наподобие коллектора, влияние этого воздушного пространства требуется оценить с использованием математической модели на основе уравнения теплопроводности, остальные процессы в первом приближении не учитываются, так как основное внимание уделяется учету инер- ции теплопередачи.

Отметим, что при стандартном подходе к выводу уравнения теплопроводности используется закон Фурье. Применение закона Фурье предполагает, что имеет место бесконечная скорость распространения тепла в среде [6. С. 40]. В случае, когда требуется учи- тывать конечность скорости распространения тепла, т.е. инерцию распространения тепла, следует модифицировать закон Фурье.

В связи с учетом инерции передачи тепла в законе Фурье появляется дополнительное выражение в правой части, и закон Фурье после модификации примет вид:

1 лт    9 q q = -kgradT - тг —, ' а t где q — вектор плотности теплового потока, т.е. количество энергии, проходящей в едини- цу времени через единицу площади, k — коэффициент теплопроводности, T — температура, тг — время релаксации тепловых напряжений.

С учетом инерции теплопередачи уравнение теплопроводности при наличии источни-

ков тепла с известной плотностью запишется в следующем виде [6]:

(ат сР dt + т

:

= div ( kgradT ) + f + т _г

d f а t ’

здесь f определяет мощность внутренних источников теплоты, c — удельная теплоем- кость, р — плотность среды.

Приведенное выше уравнение теплопроводности является гиперболическим уравнением теплопроводности, оно учитывает конечность скорости распространения тепла. Положим для простоты р = 1.

Для двумерной задачи в отсутствие источников тепла и при допущении постоянства k будем иметь уравнение вида:

^< а ² и

а и

а и       а2 и , c ;^7 + Trc -^ = к —+— ■

х аx

аy2)

Для одномерной задачи при тех же предположениях будем иметь уравнение вида:

а и      а2 и , а2 и c + тс—т = к — а t       а t2 аx2

При решении этого уравнения, как правило, используют следующие начальные усло-5 u вия u(x,0) = ф(x), ~(x,0) = 0(x) и граничные условия u(x, t) = /(t) на границе G.

Уточним граничные условия для постановки нашей задачи, будем считать, что изнутри одномерный стержень, простейшая модель оконного простенка, имеет на соответствующем конце температуру, изменяющуюся со временем по следующему закону u ( x , t ) = / ( t ), а снаружи — температуру равную температуре внешней среды.

Интерес представляет изучение распределения температуры согласно гиперболическому уравнению теплопроводности вдоль стержня в зависимости от времени релаксации.

Расчеты на основе гиперболического уравнения теплопроводности

Для упрощения расчетов и фокусирования внимания на исследовании влияния времени релаксации на результаты положим в нашей модельной задаче, что к=с=1.

Заменим уравнение его сеточным аналогом, используя:

5 u u ^¹ - u^ j

,

5 t         h_t

„ 2           к + 1          k , к - 1

52 u = ui, j - 2 ui, j + ui, j d t2 "          h2          ’

5 ² u = ^u , 4i, j ^{- 2 u} ,^kj ^{+ u}ti,j

5 x ² "           h x          .

Получим с учетом наших предположений сеточное уравнение

u

к + 1

i , j

^^^^^^е

^{k u}i , j

(., к+1   к» А  । к — -1 А ui,j - 2ui,j+ ui,j

- ^{2 u}i j ⁺ «Lu²

ht

r

h t

h

x

Согласно рекомендациям [6] при численном решении сеточного уравнения использовались те же ограничения на шаг по времени, что и при решении стандартного уравнения теплопроводности по явной схеме, в случае гиперболического уравнения теплопроводности шаг по времени существенно зависит еще от времени релаксации.

С использованием записанного выше сеточного уравнения и наших допущений было проведено численное моделирование с использованием программы, написанной на С++. При компьютерном моделировании с учетом времени релаксации были получены результаты, представленные на графиках (рис. 1, 2).

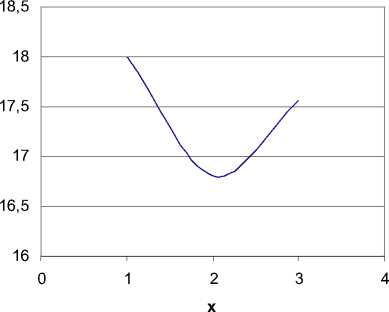
Рис. 1. Распределение температуры на временном слое при времени релаксации 0,005

На графике представлены результаты расчета изменения температуры на слое с учетом релаксации. В расчетах принималось, что с внутренней стороны нашего коллектора подается тепло, и температура на границе становится 18 градусов, в то время как на противоположной границе температура равна 10 градусам. Оказалось, что вследствие учета времени релаксации температура при всех прочих условиях меняется не сразу, как и ожидалось, наблюдается излом температуры, об этом возможном явлении упоминается также в [3]. Отметим, что приведенные гафики педставлены для асчетов при временных слоях с одинаковым номе лаксации, поэтому сами моменты времени р

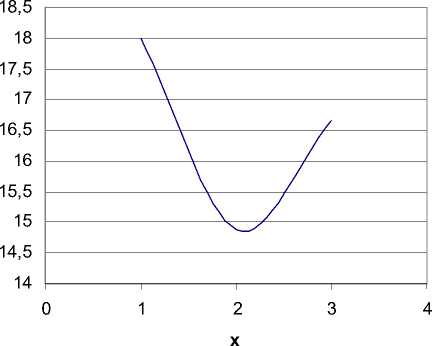
Рис. 2. Распределение температуры на временном слое при времени релаксации 0,001

Ввиду того, что изменение времени релаксации влияет на величину шага по времени, не имеет смысла отображать полученные результаты при разных величинах времени релаксации температурного напряжения на одном графике. Расчеты показывают, что во всех случаях наблюдается излом температур. Чем меньше время релаксации, тем сильнее излом. В нашей задаче предполагается, что на холодную прослойку воздуха между двумя оконными конструкциями с одной стороны подается тепло. При компьютерном моделировании время релаксации температурного напряжения являлось входным параметром.

Анализ результатов и выводы

Полученные результаты имеют важное теоретическое и практическое значение. На основе проведенных расчетов можно утверждать, что использование гиперболического уравнения теплопроводности, мало распространенного в литературе, имеет смысл. Результаты расчетов адекватно отражают картину распределения тепла, когда ввиду инерции температура не сразу передается по следующим слоям. Температура терпит излом, причем чем меньше время релаксации, тем быстрее происходит этот излом, затем происходит восстановление значений температуры к ожидаемым значениям. Практическое значение состоит в том, что на практике необходимо учитывать время релаксации и явление инерции теплопередачи, особенно для тех объектов, температурный режим которых должен поддерживаться на определенном уровне. Особое значение имеет учет инерции теплопередачи при расчете эффективности солнечных коллекторов.