Математическое моделирование процессов нитрификации и окисления органических веществ в проточной биосистеме

Проточные биосистемы, к которым можно отнести и систему биологической очистки сточных вод активным илом, представляют значительный интерес как для биологов, экологов, так и для специалистов в области математического моделирования. Для последних это связано с постановкой новых математических задач и разработкой методов исследования динамики соответствующих процессов.

Для описания такого рода процессов обычно используют системы нелинейных дифференциальных уравнений. Из-за сложности моделей, недостатка экспериментальных данных параметрическая идентификация таких систем является трудноразрешимой задачей. В данной статье предложена модель процесса биоочистки и подход к решению задачи параметрической идентификации.

ОПИСАНИЕ ПРОЦЕССА

На большинстве очистных сооружений сточная вода, пройдя предварительные этапы обработки, попадает в специальные резервуары, аэротенки, где происходит биологическая очистка. В работе рассмотрен процесс, происходящий в аэротенке-смесителе, в который активный ил и сточная вода поступают непрерывно. Иловая смесь движется вдоль оси аэротенка. Сточная вода, содержащая разные виды субстрата, поступает с одинаковой объемной скоростью равными порциями в нескольких точках аэротенка.

На рис. 1 приведена схема аэротенка очистных сооружений г. Петрозаводска. Выделим два вида субстрата, которые окисляются на очистных сооружениях:

• •    органический субстрат, характеризуемый концентрацией S_S ;

• •    азот в аммонийной форме, характеризуемый концентрацией S_NH .

Очистные сооружения, как правило, успешно справляются с окислением органического субстрата, достаточная же степень окисления аммония может не достигаться. Возникает проблема математического моделирования процесса нитрификации с целью уменьшения величины ^S NH в очищенной воде.

дит идеальное перемешивание иловой смеси, которой на прохождение каждого компартмента требуется время t i = k • t_el . За время t i в C i вливается сточная вода объемом V cv, i = k • V cv •

Пусть ^S S ’ ^S NH и ^S S , i , ^S nh , i — концентрации субстратов в сточной воде и иловой смеси на выходе из i -го компартмента соответственно, X H , i , X A , i – концентрации гетеротрофных и автотрофных микроорганизмов иловой смеси на выходе из i -го компартмента соответственно.

При попадании иловой смеси в следующий компартмент, где она перемешивается со сточной водой, концентрации субстратов и микроорганизмов активного ила на входе в i + 1 -й ком-партмент рассчитываются по формулам:

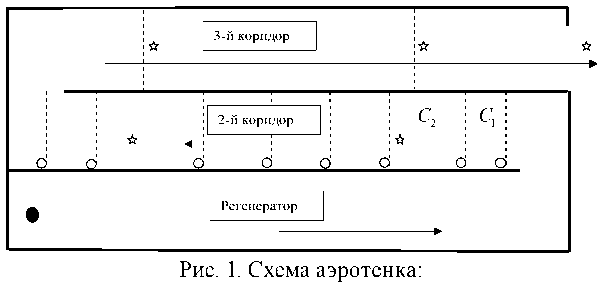
– место вхождения сточной воды в аэротенк;

– место вхождения иловой смеси в аэротенк;

– место отбора проб;

– направление движения иловой смеси;

– границы компартментов

s * • V _v, + s_v • ■ v

1 in __ S cv , I S , I I in in

' S , i + 1 =         77     , т/ ’ ^SNH , i + 1

V cv, i ⁺ V i

^SNH ' ^Vcv , i ^{+ S}NH , i ' ^Vi

V cv , i + V i

, (1)

В аэротенке выделим участок длиной l_el (на-

пример, l_el = 1 м) и объем V_d = a • b • l_el , где a

–

ширина коридора аэротенка, b – высоты иловой смеси в аэротенке. Пусть за время A t в систему попадают объемы A V_v , A V сточной воды и ак-A V Г ■ 1

и

in

H, i + 1

X H,.• ^V i   X„I = XAr ^V i

V ,   ^{A,i + 1} К -+K^.

cv, г         г                               cv, г         i

тивного ила соответственно. Тогда v =  —

At v = il — объемные скорости вхождения в аэ-

²     A t

ротенк сточной воды и активного ила соответст-V венно. 11 = —-— — время продвижения иловой

V1 + V 2

смеси на расстояние l_el . Учитывая, что сточная вода подается через n труб, рассчитаем объем, который входит через одну трубу за время t_el :

V = Vik cv

.

n

Иловая смесь, двигаясь по коридору аэротенка, попадет к месту вхождения сточной воды (через очередную трубу), где происходит их перемешивание. Таким образом, места вхождения сточной воды естественным образом делят аэротенк на компартменты ( C i , i = 1,2, ...), объемы которых равны V i = k i • V_el , где k i - количество участков длиной l_el , входящих в C i Будем предполагать, что в каждом компартменте происхо-

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

Группой исследователей во главе с M. Henze был предложен ряд моделей для описания процесса биоочистки [7]. Их подход носит методологический характер и указывает направления для получения конкретных моделей. На основании подхода, предложенного этой группой, разработана модель, учитывающая динамику концентраций органического субстрата, азота в аммонийной форме и микроорганизмов, окисляющих эти субстраты.

В активном иле выделим 2 группы микроорганизмов: гетеротрофные и автотрофные. В общей биомассе гетеротрофов значительно больше, чем автотрофов [8]. Гетеротрофные микроорганизмы преимущественно окисляют органический субстрат, обеспечивая за счет этого рост своей биомассы. Концентрацию органического субстрата будем характеризовать показателем БПК_полн (полное биохимическое потребление кислорода для окисления субстрата). Однако последний показатель включает в себя расход кислорода и на процессы окисления других веществ, в том числе тех, которые не будут окислены в аэротенке. Поэтому введем пороговую функцию f 1 , позволяющую описать переключение процесса окисления с органики на аммоний азота при достижении концентрацией S_S некоторого значения c + б . В качестве значения c можно взять БПК полн надиловой жидкости на выходе из аэротенка. Константа б >  0 — достаточно малая величина, которая обеспечит ограничение на уменьшение концентрации S_S до величины чуть большей c , что необходимо для непрерывности предложенной ниже математической модели. Значение б = 10 ^{- 3} при проведении компьютерных экспериментов оказалось

вполне достаточным. Пусть f 1  ---- 7775— . По.                   1 + e'° *

ведение функции fx имеет ступенчатый харак тер. При этом fl ® 0 при SS е (0, c + - - s), f ® 1 при SS е (c + - + s,«), где s > 0 - достаточно малая величина. Константа 106 обеспечивает близость функции f к разрывной ступенчатой функции.

Наличие органических веществ активизирует развитие гетеротрофных микроорганизмов, которые выигрывают у нитрифицирующих микроорганизмов в борьбе за кислород [2]. В результате процесс нитрификации сначала в значительной мере затормаживается и начинает активизироваться по мере удаления органического субстрата. Введем функцию, отражаю- щую этот факт: f, = —SNHZISS—с)—, где Ka-Ка + Snh / ( Ss - с)

некоторая постоянная. Заметим, что f , е (0, 1), f , возрастает при увеличении отношения концентраций S_NH / ( S S - с).

Используя зависимость Моно f ( S , K ) ----- и введенные выше функции f 1 , f , , получаем динамическую систему, описывающую процесс биоочистки в компартменте:

- Q ( S‘_s" - S ,) - —f ( S ,, K_s ) f ( So , K_o и )-----Цг- Xн ,

S          S S                 S , S O , O , H                        H ,

Y„                                      i0⁶( - i)

HS

1 + e S

Snh=Q(S™h-Snh)-

*Л                            ⁺ ^NH ' ws ^c)

(

10⁶( ^{- + -} - 1) 1 + e     ^S S

X H - Q ( X H

X h ) + _MH f ( S S , K s ) f ( S o , K oh ) I

>

- b H X H,

X ^ a = Q ( X A - X a ) + ( H A f ( S nh , K nh ) f ( S o , K o a ) „ S;. '⁽ SS, „ ) , "  Ь а I X a , v                             ^K a ⁺ S NH / ⁽ S S ) )

где Q - 1 [1] — расход смеси ила и сточной воды, T – время прохождения аэротенка иловой смесью, S_O – конрастворенного кислорода;

Концентрации соответственно на входе и выходе компартмента: SSn, SS - растворенных органических веществ; SNH, SNH - растворенного азота в аммонийной форме; XH, XH - гетеротрофных микроорганизмов; X™, XA - автотроф- ных микроорганизмов.

Параметры модели: KS – константа полунасыщения гетеротрофов органическими веществами; KNH – константа полунасыщения автотрофов аммонием азота; KOH - константа полунасыщения гетеротрофов , кислородом; KO,A - константа полунасыщения автотрофов кислородом; YH – константа перехода массы органического субстрата в биомассу гетеротрофов; YA – константа перехода массы аммония азота в биомассу автотрофов; bH– скорость рас- пада гетеротрофов; bA – скорость распада автотрофов; Мн - максимальная скорость роста гетеротрофов; Мл - максимальная скорость роста автотрофов.

Для нахождения концентраций на выходе из каждого компартмента производится численное интегрирование системы (2). Результаты интегрирования с использованием параметров из таблицы представлены на рис. 2 и 3. Концентрации на входе в каждый компартмент вычисляются по формулам (1). На рис. 2 показано изменение концентраций в первом компартменте, причем характер изменения сохраняется для всех ком-партментов, которым на вход подается сточная вода. В остальных компартментах изменение концентраций монотонно. Рис. 3 отражает изменение концентраций во времени при прохождении выделенного объема смеси через аэротенк (по всей длине). «Всплески» соответствуют моментам времени прохождения этим объемом участков входа сточной воды.

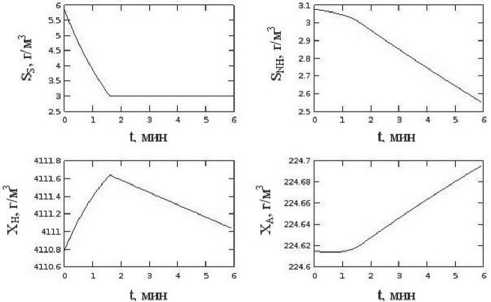
Рис. 2. Динамика концентраций в первом компартменте

Следует отметить, что представленная в данной работе модель позволяет более адекватно описывать процессы окисления органики и нитрификации по сравнению с моделью из [6], что достигается введением соответствующих пороговых функций.

ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ

Задача параметрической идентификации математических моделей процесса биоочистки является сложной проблемой в силу следующих причин:

• •    невозможность учесть в модели все происходящие процессы;

• •    труднодоступность, а иногда невозможность получения экспериментальных данных;

• •    «зашумленность» имеющихся данных.

В связи с недостатком экспериментальных данных большинство методов параметрической идентификациинеприменимы.Длярешениязада-чи использован метод сканирования [3] в области допустимых значений параметров, определенной с использованием полученных в [8] резуль- татов. Решением является набор параметров P = (YH , YA , Hh , И A , bH , bA , KS , KNH , KO,H , KO, A , Ka ) , который минимизирует целевой функцио-ny⋅N нал J = £ wi(yi - ym)T (yi - ym), где Wj - весо вой коэффициент, ny – количество наблюдаемых переменных, N – количество точек сбора экспериментальных данных, yi, yim– экспери- ментальные и модельные данные соответственно. Численное моделирование проводилось с помощью кластера «Центра высокопроизводительной обработки данных» (ЦКП КарНЦ РАН, 2012–2013). Получение модельных данных проводилось путем решения системы (2) методами прогноза и коррекции и Адамса.

При получении экспериментальных данных общепринятая в практике допустимая погрешность г по концентрации аммония составляет ±0, 5  3 , по концентрации микроорганизмов – 14 %. м

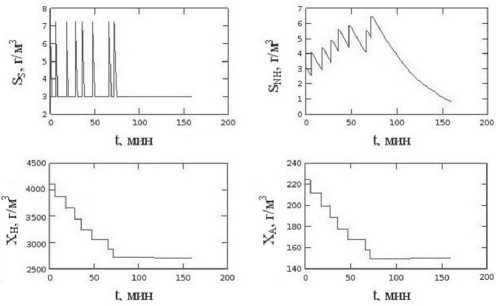
Рис. 3. Динамика концентраций в выделенном объеме иловой смеси в зависимости от времени прохождения им различных участков аэротенка

Проведены компьютерные эксперименты, в которых экспериментальными данными были: БПКполн на выходе из аэротенка; концентрации аммония азота y, и общей биомассы микроорганизмов y2 на входе, в четырех точках аэротенка и на выходе из него. Эти данные были получены на очистных сооружениях г. Петрозаводска в 2012 году. С помощью метода сканирования был получен набор параметров, минимизирующий целевой функционал J.

Значения параметров

Параметр	Значение	Единицы измерения
Y H	0,38	г биомассы · (г БПКполн) –1
Y A	0,24	г биомассы · (г аммония азота) –1
μ H	5,5	сут.-1
μ A	0,58	сут.-1
b H	0,05	сут.-1
b A	0,05	сут.-1
K S	93	г БПКполн · м–3
KNH	4,7	г аммония азота · м–3
KO,H	0,05	г 02 · м–3
KO,A	0,77	г 02 · м–3
K α	5	безразмерная величина

ВЫВОДЫ

Предложена математическая модель процесса биоочистки, учитывающая окисление органики, аммония азота и динамику биомассы активного ила. При этом используется компарт-ментальный подход. Специфика моделируемого объекта позволяет редуцировать базовую модель, предложенную в [7], и рассматривать систему, содержащую меньшее количество дифференциальных уравнений. В результате появляется возможность параметрической идентификации модели при небольшом количестве экспериментальных данных. С помощью метода сканирования найден набор параметров, наиболее удовлетворяющий экспериментальным данным.

Возможно дальнейшее уточнение значений параметров с использованием теории чувствительности [4], [5]. Предполагается развитие модели путем введения уравнения динамики концентрации кислорода, что позволит решить задачу управления процессом биоочистки.

* Работа выполнена при поддержке Программы стратегического развития ПетрГУ рамках реализации комплекса мероприятий по развитию научно-исследовательской деятельности на 2012–2016 гг.

MATHEMATICAL MODELING OF NITRIFICATION AND ORGANIC MATTER OXIDATION PROCESSES IN FLOW-THROUGH BIOSYSTEM