Математическое моделирование процессов пластической деформации ГЦК-материалов в условиях изменяющейся скорости деформирования

Кристаллографическое скольжение практически всегда сопутствует другим явлениям, обеспечивающим макроскопическое формоизменение кристаллов, и обычно является доминирующим процессом пластичности кристаллов. Основой элементарных механизмов и процессов пластической деформации скольжения являются возникновение, размножение, движение и аннигиляция дефектов различного типа. По этой причине при построении кинетических моделей пластичности весьма эффективно используются уравнения баланса деформационных дефектов [1-24]. Различные модели отличаются прежде всего набором деформационных дефектов и рассматриваемых механизмов их образования и аннигиляции.

Заметим, что роль и возможности математического моделирования и вычислительного эксперимента в ходе анализа закономерностей пластической деформации при различных приложенных воздействиях трудно переоценить. Именно математическое моделирование позволяет выявить роль различных факторов, характеризующих материал и воздействие на него, в формировании закономерностей и особенностей реализации и доминирования различных механизмов и процессов пластической деформации в деформационном упрочнении и эволюции деформационной дефектной среды кристаллических материалов и способствует целенаправленному планированию экспериментальных исследований.

Одной из наиболее развитых математических моделей, включающих уравнения баланса деформационных дефектов, является математическая модель пластической деформации скольжения [10-24], основанная на концепции упрочнения и отдыха [1-3], согласно которой пластическое поведение кристаллических материалов есть результат наложения атермического упрочнения в результате накопления деформационных дефектов и температурно-зависимого разупрочнения, связанного с термически активируемыми процессами залечивания поврежденной структуры (аннигиляции деформационных дефектов).

В качестве базового структурного элемента, относительно которого ведется рассмотрение механизмов сдвиговой пластичности в модели [10-24], выбрана зона кристаллографического сдвига. Описание механизмов и закономерностей генерации, аннигиляции и взаимной трансформации деформационных дефектов различного типа базируется на фундаментальных физических и топологических свойствах дефектов, осуществляющих пластический массоперенос. Все параметры модели имеют физический или геометрический смысл и могут быть вычислены из физических соображений либо может быть указан интервал их возможных значений. Математическая модель включает уравнения баланса достаточно полного набора деформационных дефектов, порождаемых при кристаллографическом скольжении. Частные модели механизмов генерации и аннигиляции деформационных дефектов и математические модели пластической деформации скольжения для ГЦК-металлов и дисперсно-упрочненных сплавов записаны на основе единых предположений [10-24]. Математическая модель пластичности скольжения в различных модификациях применялась для описания пластического поведения ГЦК-металлов и сплавов при различных воздействиях (ползучесть, релаксация напряжений, деформация с постоянной скоростью деформирования и др. [10-24]).

Используемая в настоящей работе математическая модель пластической деформации скольжения [12-13, 21-24] содержит уравнения, описывающие: приложенное воздействие, которое является причиной пластической деформации; отклик деформируемого материала на деформирующее воздействие (уравнение, связывающее скорость деформации с переменными, характеризующими приложенное воздействие и деформационную дефектную среду); кинетику деформационных дефектов в материале. Предполагается, что процесс деформации во всех действующих системах осуществляется в идентичных зонах сдвига. Деформационная дефектная среда, формируемая в зонах кристаллографического сдвига, заменяется однородной деформационной дефектной средой.

Для реализации математической модели создан пакет прикладных программ [25], позволяющий численно исследовать закономерности пластической деформации и эволюции дефектной подсистемы монокристаллов ГЦК-металлов и дисперсно-упрочненных сплавов в условиях деформации с постоянной скоростью деформирования, ползучести при постоянном напряжении и постоянной нагрузке (в условиях растяжения и сжатия), а также при деформации с изменяющейся скоростью деформирования.

1.    Математическая модель

В качестве переменных, характеризующих дефектную среду ГЦК-металлов, в математической модели пластической деформации скольжения выбраны следующие: плотность сдвигообразующих дислокаций ( р m ), плотность дислокаций в дипольных конфигурациях ва-кансионного ( p d ) и межузельного ( р d ) типа, концентрации межузельных атомов ( с , ), моновакансий ( с 1 v ) и бивакансий ( с ₂ v ). Математическая модель может быть представлена в следующем виде [12-13, 21-24]:

d^m = (i - «sPas )FT — 27 Pm min(ra , P.. 'И ( 1 — ®s )?m Ь' (СЙ + da          Db ab

+ 2 c 2 v Q 2 v ) + c . c i v ® Q + c 2 v c, ® im Q ₂ v + c i v <  ( p „s b ² + 2 c i v + c i ) Q i v +

8 ЛТ, ( 1 — V )

⁺ c i ^c iv ® m Q i ^{+ 2} c i ^c 2 v ®_mQ i} ⁺ —77j7 ---V^[ ® dv c i v ⁽ p ns b ^{+                   (1)}

aGb ( 2 — v )

+ 2 c i v + c , ) Q i v + ®X c i v c , Q i + 2 c 2 v p dv b ² Q 2 v + 2 ® 2 v c 2 v c , Q i +

^{+ c} i P di b ² Q i ⁺®‘^ Q i v ⁺® Vic 2 v ^Q 2 v ]•

² P d_      ⁱ        8^ЛТ f ^{( i — V}L _n v ,2

“7 „ / ML\[ cip 2b Qi+® dv ci(ci v Qiv + c 2 v Q2 v ) + da   6ydtd(p)b aGb (2 — v)

+®2vv civ ((p ns b 2 + 2 civ + ci) Qiv + ci Qi) + 2 c 2 v (pdb 2 + ci) Q2 v +

+ 2 ® dv c 2 v c i Q i ].

dp'i,         i         8лт f (i — v),

-Td “            —               [®dvciv (( pnsb + 2civ + ci )Qiv + ciQi) + da   6ydtd(p)b aGb (2 — v)(3)

+2 c 2 v pvb 2 Q2 v + 2® dvc 2 vc, Q. + cpdb 2 Qi +® dici^ ci vQiv + c 2 v Q2 v )]• dEt “ q     — i[ci(p „sb 2 + civ + c 2 v ) Qi+ civ Qiv + c 2 v Q2 v ]• da    Ga dciv_ “q!^, — ![civ (pns b2 + 2cv, + ci)Qiv + c,(civ — c2v)Qi — c,c2vQ2v ]•(5)

da   6Ga dT^ = 5q -Tdn — 2[ c 2 v (pns b2 + c. ) Q2 v + c, Qi ) — ci v civ Qiv ]•(6)

da 6 G a

_8p r 2 ( т-Т a ) 1X b 2^3 p^ B_r Т e Г U — ( Т — Т a ) Х ( т , p ) p^{— i/2} bb k (1 — p _r ) ^2/3 ^ ^i/6 G ^4/3Х( т , p ) F p [               kT

Здесь [I0-I3, 26-27] a - деформация сдвига, U(m) - энергия миграции точечного дефекта j-го типа, ®s - доля винтовых дислокаций, ®nj - доля точечных дефектов j-го типа, ушедших на стоки „-го типа, значение F определяется формой дислокационных петель и их распределением в зоне сдвига, pr - доля реагирующих дислокаций леса, к - постоянная Больцмана, тa - атермическая составляющая сопротивления движению скользящей дислокации, т dy„ - разность между деформирующим напряжением и сопротивлением движению дислокаций при формировании зоны сдвига, для квазистатических условий деформации тdyn = ad,nGbp1/2, т - деформирующее напряжение, тf- напряжение трения,

G - модуль сдвига, a - деформация сдвига, Qj = vdZ exp(-U(m) / kT), vD -частота Дебая, b - модуль вектора Бюргерса, pns = ((1 юs)pm + pd), Pd = pd + Pd, D = Brт/(Gbp) - диаметр зоны сдвига, Br - вычисляемый параметр, v - коэффициент Пуассона, £ - доля дислокаций леса, q -параметр интенсивности генерации точечных дефектов, £ d - длина пробега винтовых компонент дислокации, U = 0,2Gb3 - энергия активации преодоления стопора, ar - параметр, характеризующий интенсивность взаимодействия скользящей дислокации с реагирующими дислокациями леса

Мт, p) = Ма r р r У1/3 +

1/3

( Т-Т _а )(1 -Р r )

§1/2 Gb p1/2

^ 1/2

Уравнение (7), связывающее скорость деформации, напряжение и плотность дислокаций, в случае деформации с постоянной скоростью деформирования является нелинейным уравнением, позволяющим определить текущее напряжение.

2.    Описание программного комплекса SPFCC

Для поддержки пользователя при работе с представленной выше математической моделью для металлов с ГЦК-структурой и моделью для исследования закономерностей пластического поведения дисперсно-упрочненных материалов с ГЦК-матрицей создан комплекс программ Slip Plasticity of Face-Centered Cubic (SPFCC). Комплекс программ SPFCC является программным инструментом, который позволяет проводить компьютерные эксперименты для различных приложенных воздействий (деформация с постоянной скоростью деформирования, при постоянном приложенном напряжении и при постоянной нагрузке в условиях растяжения и сжатия) и их комбинаций [25]. На рис. 1 приведено главное окно комплекса программ.

При помощи комплекса программ SPFCC пользователь может провести моделирование, используя как полную модель (1)-(7), так и формируя редуцированные модели, в которых будут учтены указанные им деформационные дефекты и механизмы их генерации и аннигиля- ции, получить численное решение, визуализировать полученные результаты (в том числе и в режиме реального времени).

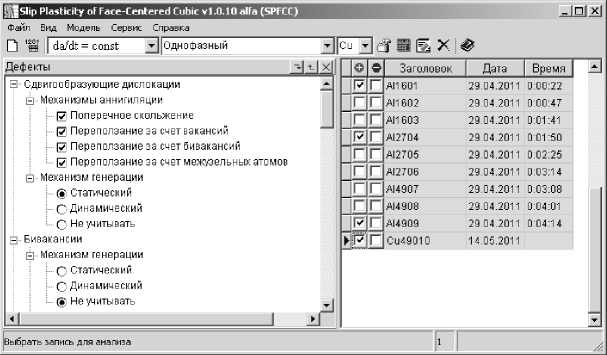
Рис. 1. Главное окно программы SPFCC

Отметим, что система ОДУ баланса деформационных дефектов для различных деформирующих воздействий и материалов может отличаться числом уравнений и представленных в них механизмов образования и аннигиляции дефектов, кроме того, уравнения могут быть кусочно-сшитыми, что накладывает ряд ограничений на выбор численного метода. Система дифференциальных уравнений модели является жесткой [28, 29]. Это связано прежде всего с тем, что процессы генерации и аннигиляции деформационных дефектов являются существенно разноскоростными, переменные системы являются разнопорядковыми величинами и изменяются на интервале интегрирования на порядки величины. В программном комплексе SPFCC для решения жесткой системы ОДУ использованы: явный линейный многошаговый метод Адамса (нахождение точек разгона) и линейный многошаговый метод Гира переменного порядка (в виде формул дифференцирования назад), который устойчив при любой величине шага интегрирования, и поэтому шаг интегрирования можно выбирать, руководствуясь лишь соображениями точности, а не устойчивости [28]. Классический метод Гира модернизирован [25], поскольку на переменные системы уравнений накладываются некоторые физические ограничения (например, значения переменных не могут быть отрицательными). В работах [28, 29] приведен анализ эффективности используемых численных алгоритмов на примере математической модели пластической деформации для дисперсно-упрочненных материалов с недеформируемыми частицами.

Взаимодействие с пользователем реализовано через многооконный графический интерфейс (см. рис. 1). Используя диалоговое окно «Менеджер входных данных», пользователь может задать значения параметров математической модели, начальные условия, точность проведения расчетов (рис. 2, 3). После выбора материала для некоторых параметров математической модели система предлагает пользователю выбрать значения параметров из определенного набора значений (представленных по результатам теоретических и экспериментальных исследований различных авторов или из справочной литературы) либо задать значения самостоятельно. Далее программно осуществляется проверка элементов графического интерфейса на допустимость введенных данных, и при необходимости данные, введенные пользователем некорректно, корректируются, а пользователю выдается информационное сообщение. Пользователю также предоставлена возможность выполнения серии вычислений (см. рис. 2), при этом необходимо указать параметр математической модели (напряжение, температура, начальная плотность дислокаций и др.), интервал и шаг изменения этого параметра.

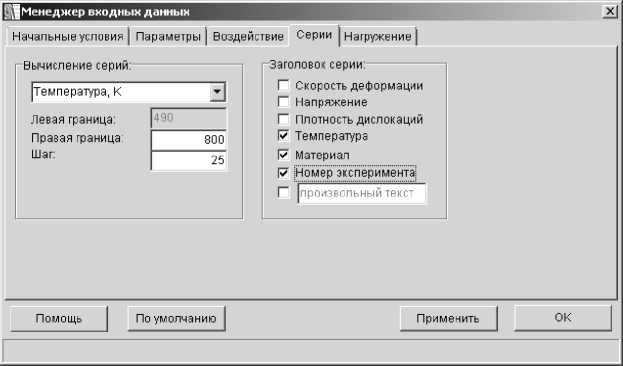
Рис. 2. Диалоговое окно «Менеджер входных данных», вкладка «Серии»

За счет объединения под одной управляющей программной оболочкой с единым графическим интерфейсом модуля ввода данных, расчетного модуля, модуля взаимодействия с базой данных (запись, чтение, редактирование) пользователь может осуществлять моделирование без опыта программирования и работы с численными методами.

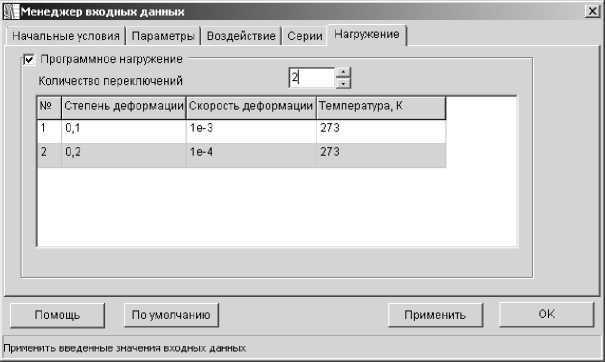
Рис. 3. Диалоговое окно «Менеджер входных данных», вкладка «Нагружение»

В ходе расчетов возможна визуализация промежуточных результатов моделирования в режиме реального времени, что позволяет контролировать ход вычислений (рис. 4). Результаты моделирования вместе с использованными при проведении вычислительного эксперимента значениями параметров модели сохраняются в локальной базе данных. В базе данных также сохраняется информация о ходе численного решения задачи. Эта информация позволяет сформировать рекомендации для проведения дальнейших компьютерных экспериментов.

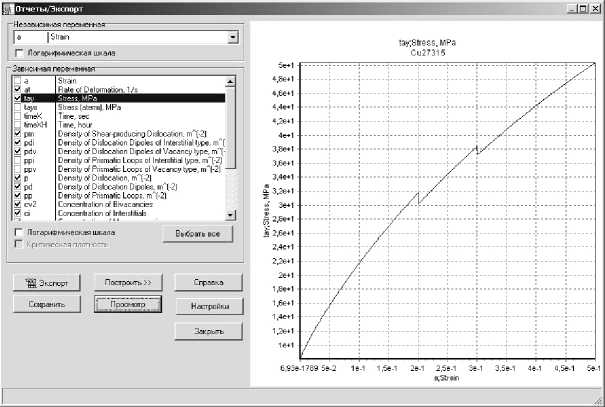
Рис. 4. Диалоговое окно «Отчеты/Экспорт»

В комплексе программ SPFCC реализована возможность сравнения (в табличном и графическом видах) результатов моделирования для различных приложенных воздействий или их комбинаций. По результатам моделирования могут быть представлены графически не только зависимости между любыми переменными, но и температурная и скоростная зависимости (см. рис. 4). Табличное представление результатов расчетов предназначено для экспорта данных в программные продуты сторонних разработчиков для дальнейшей обработки (например, MS Excel, OpenOffice Calc, Origin).

3.    Влияние скорости деформации на закономерности пластического поведения монокристаллов ГЦК-металлов

Для деформации с постоянной скоростью деформирования система (1)-(6) представляет собой жесткую систему обыкновенных дифференциальных уравнений баланса деформационных дефектов, замкнутую нелинейным уравнением (7) для определения напряжения течения.

При компьютерном моделировании были использованы следующие значения параметров модели: F= 4,7, ю = 0,3, 0 r =0,14, т f =1 МПа, § = 0,5, B r =800, v= 0,33, b= 2,540 " ¹⁰ м^-2 [10-13, 26-27]. Все параметры модели получены из результатов независимых исследований или из справочной литературы. В качестве начальных значений переменных модели (1)-(7) выбраны следующие: c i = c v = c _{2 v} = 0, p d = p d = 0, p m =10¹² м^-2.

Для определения интервала скоростной зависимости напряжения течения в условиях деформации с постоянной скоростью деформирования проведено моделирование для никеля при различных температурах и степенях деформации (рис. 5). Область выраженной скоростной зависимости для никеля в исследованном интервале температур наблюдается при температуре 500 К. Дальнейшие вычислительные эксперименты были проведены для диапазона скорости деформирования от 10-2 с-1 до 10-4c-1.

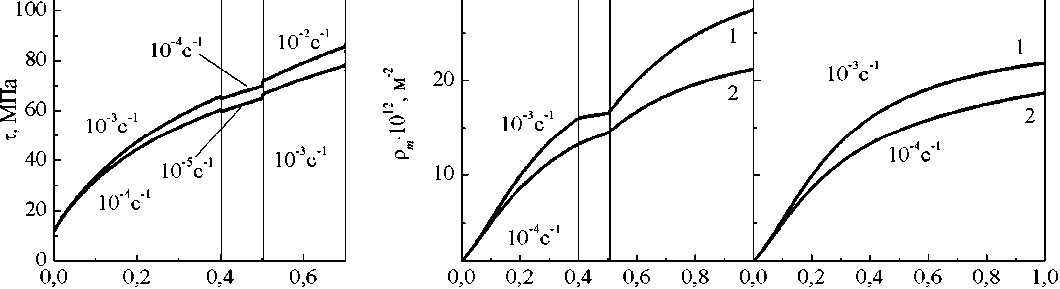
На рис. 6 представлены результаты моделирования пластической деформации монокристалла никеля с постоянной скоростью деформирования при использовании следующей программы воздействия на материал. При достижении степени деформации сдвига 0,4 происходит скачкообразное снижение скорости деформации на один порядок. Далее продолжается деформирование с пониженной скоростью до степени де- формации сдвига 0,5, при достижении которой скорость деформации скачком увеличивается на два порядка (рис. 6, a, 6). Для сравнения на рис. 6, в приведены результаты моделирования при постоянной скорости деформации на всем протяжении компьютерного эксперимента.

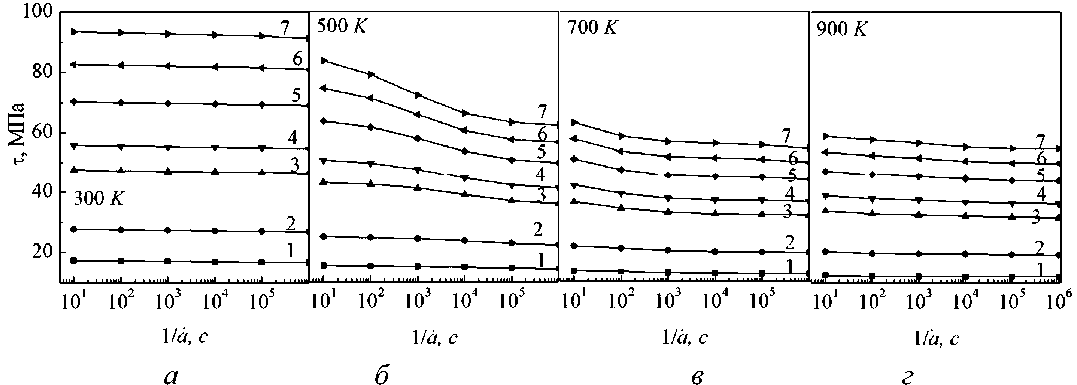
Рис. 5. Скоростная зависимость напряжения течения при температурах: 300 K ( a ), 500 K ( 6), 700 К ( в ) и 900 К ( г ) для никеля при степенях деформации (цифры у кривых): 1 - 0,01; 2 - 0,05; 3 - 0,15; 4 - 0,2; 5 - 0,3; 6 - 0,4 и 7 - 0,5

зо

а                              6                     в

Рис. 6. Деформация никеля с постоянной скоростью деформирования при температуре 500 K со скачкообразно изменяющейся скоростью деформации: а - напряжение течения; 6 , в - плотность сдвигообразующих дисклокаций. Начальная скорость деформации 10^-3c^-1 (кривая 1 ) и 10^-4c^-1 (кривая 2 )

Результаты численных экспериментов, представленные на рис. 7, 8, получены для различных ГЦК-металлов при одинаковых гомологических температурах и начальной скорости деформации 10-4с-1. В процессе деформации скорость изменялась следующим образом (см. рис. 7, 8): кривая 1 - постоянная скорость деформации 10 4с 1 на всем интервале; кривые 2, 3 - при достижении степени деформации 0,2 скорость деформации скачком увеличивалась с 10 4с 1 до 10-3с-1; кривая 2 - при степени деформации 0,4 скорость деформации скачком увеличивалась до 10-2с-1; кривая 3 - при степени деформации 0,4 скорость деформации скачком снижалась до 10-4с-1.

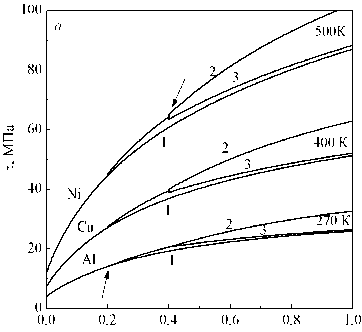
Рис. 7. Напряжение течения никеля, меди и алюминия при начальной скорости деформации 10-4с-1

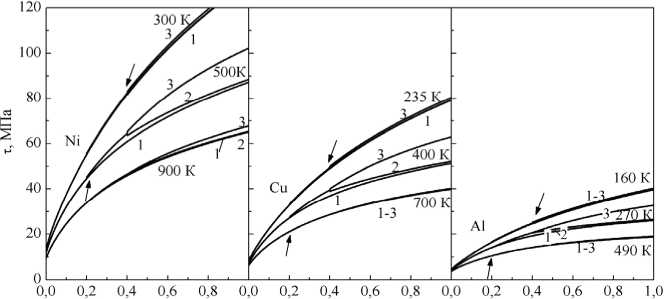
а                       б                      в

Рис. 8. Кривые течения для монокристаллов никеля, меди и алюминия при различных температурах: а - 300 К; б - 235 К; в - 160 К.

Условия вычислительных экспериментов соответствуют рис. 7

Увеличение скорости деформации при достижении степени деформации сдвига 0,2 на один порядок величины с 10^-4с^-1 до 10^-3с^-1 приводит (см. рис. 7, кривые 2 ) к увеличению напряжения течения при степени деформации 0,4 на 3,1 МПа (8 %) для меди, на 4 МПа (6 %) для никеля и на 1 МПа (5 %) для алюминия по сравнению с напряжением течения, полученным при постоянной скорости деформирования 10^-4с^-1

(см. рис. 7, кривые 1 ). Увеличение скорости деформации при степени 0,4 еще на один порядок величины до 10^-2с^-1 приводит к еще более выраженному изменению напряжения течения по сравнению с деформацией при постоянной скорости деформирования 10^-4с^-1 (см. рис. 7, кривые 2 ). При увеличении скорости деформации на один порядок величины до 10^-3с^-1 при степени деформации сдвига 0,2 и снижении до 10с^-1 при степени деформации 0,4 напряжение течения остается несколько выше наблюдаемого при постоянной скорости деформирования (см. рис. 7, кривые 3 ). Подобная картина (см. рис. 7) наблюдается для различных металлов (никель, медь, алюминий).

При более низких температурах (300 К, 235 К и 160 К для никеля, меди и алюминия соответственно) изменение скорости деформации практически не оказывает влияния на поведение кривых деформационного упрочнения (см. рис. 8). Аналогичная картина наблюдается и при температурах 900 К, 700 К и 490 К для этих же металлов.

Заключение

Математическая модель пластической деформации скольжения для ГЦК-металлов и дисперсно-упрочненных материалов и комплекс программ для ее реализации предоставляет исследователю, в том числе и не имеющему опыта работы с дифференциальными уравнениями, возможность проведения вычислительных экспериментов для различных материалов и деформирующих воздействий. Использованная математическая модель процессов пластической деформации скольжения позволяет проследить совместное действие большого числа разнообразных факторов, как внешних, так и обусловленных структурой самого материала, при широкой вариации значений характеризующих их параметров. Представленные результаты являются примером использования средств моделирования и автоматизации исследований с использованием комплекса SPFCC, в том числе и для планирования экспериментов.