Математическое моделирование процессов сигналообразования движущихся объектов и формирования их теневых радиоизображений в просветных РЛС

Современный уровень развития вычислительной техники позволяет использовать геометрические модели, достаточно хорошо аппроксимирующие реальные объекты. Использование дифракционной формулы Френеля-Кирхгофа [1] для расчета комплексной амплитуды U(P) электромагнитного (ЭМ) поля в точке нахождения антенны приемника (ПРМ) предполагает использование в качестве поверхности интегрирования теневого контура [2] описываемого трехмерного объекта. Это обстоятельство приводит расчет комплексной амплитуды ЭМ-поля U(P) реальных объектов сложной формы к трудоемким или даже неразрешимым задачам.

Одним из возможных решений является иcпользование для описания геометрических поверхностей реальных объектов совокупности различным образом ориентированных эллиптических цилиндров. Например в [3-4] предложено моделировать нарушителя зоны охраны (ЗО) радиолокационной технической системы охраны в виде вертикально ориентированного эллиптического цилиндра при пересечении человеком – нарушителем ЗО «в рост» и в виде комбинации вертикально и горизонтально расположенных цилиндров при моделировании человека – нарушителя в положении «согнувшись». Представление объекта-нарушителя комбинацией эллиптических цилиндров позволяет обойти проблемы, связанные с его описанием в виде набора плос- костей. Данная модель позволяет достаточно просто изменять размеры, форму и ориентацию объекта относительно передатчика (ПРД) и ПРМ без изменения общего вида интеграла Френеля-Кирхгофа.

В работе [5] предложено моделировать поверхность тела человека совокупностью эллиптических цилиндров, однако такое представление поверхности имеет определенные пределы по количеству используемых эллиптических цилиндров ввиду резкого возрастания сложности описания объекта и трудоемкости вычислений.

Одним из вариантов решения задачи расчета поля объектов сложной формы (ОСФ) может быть использование метода излучающей апертуры [6], в соответствии с которой построенная трехмерная модель объекта проецируется на плоскость и представляется набором единичных излучателей Гюйгенса с известными координатами. На рис. 1 приведена схема пересечения ОСФ зоны между ПРД и ПРМ просветной РЛС. Будем считать, что координаты центра О объекта по осям X, Y и Z равны соответственно X0 ’ Уо ’ ^1 и он перемещается параллельно оси без изменения значений У О И ^ H. Векторы г и s проведены из точек Po и P" расположения ПРД и одного из ПРМ вертикальной линейки ПРМ РЛС в произвольную точку поверхности Q проекции ОСФ, через которую проходит и вектор нормали n.

Рис. 1. Формирование сигналов в точках

Pn(0,h"nPM,Rm) нахождения антенн ПРМ вертикальной линейки ПРМ просветной РЛС

Для рассматриваемого случая проекции объекта на плоскость, параллельную плоскости XOY , формула Френеля-Кирхгофа для комплексной амплитуды электромагнитного поля U(Pn) в точках p нахождения точечных [2] антенн вертикальной линейки ПРМ трансформируется к виду:

т'тпэ м - Ai ffPnp (x> y)exp[ik(r + sn)] 2л              rs                 (1)

x [cos( n, r) - cos( n, sn )]dS, где r, s – модули векторов г и sn ; к = 2n/X – волновое число; X – длина волны ЭМ-поля; A – амплитуда возмущения на расстоянии единицы длины от антенны ПРД; i = V^T; $ – площадь проекции ОСФ; dS = dxdy – элемент площади этой поверхности; ₽nP(x,y) – функция пропускания объекта.

Входящие в (1) векторы г и sn и n определяются (при отсчете координат X и у относительно центра О объекта) выражениями:

г = (x + x0)i +(у + у0 -Нпрди + RHk;

sn =(x + x0)i+(y + y0-h^M)j + (Rm -RH)k;

n = к.                                 (2)

При определении выражений для cos(n,r) и cos(n,sn) можно использовать известное свойство скалярного произведения векторов (r,n) = |r||n| cos(r, n), откуда cos(«, г) =                  H                 ;

(x + X() ) + (у + У о — ^прд ) "*" Rh cosQi,sn)

RH-Rm

•^(x + Xq) +(У + Уо ^_^7Pm) ⁺(-^»^-^я)

При использовании численных методов интеграл (1) заменяется двойной суммой, подынтегральная функция непрерывных аргументов X и Y – функцией дискретных аргументов Xj =(i-I)Ax и Yj =(j-J)Ay, где Ax и Ay – шаг дискретизации для X и у соответственно. Расчет дифракционной картины производится для области значений ^x0m =(m-MW₀, где m = 0,1...2M, а Ax₀ – шаг дискретизации переменной x₀ . В случае эквидистантного (по высоте) размещения ПРМ с шагом ^Ah_nPM величина ^ПРМ ^— ^ПРМ + (ⁿ '^)^¹ПРМ ’ где h_npM – координата по оси Y середины линейки ПРМ, n = 0,1...2N . С учетом введенных обозначений (1) преобразуется к виду

U(x_Om,hn_PM) = U(m,n) =    £^y5_np(i, j) x

2-A j_{=0 /=0}

exp[-ik(^(x,. +x_0m)² +0л + y„ -h_n,,,y +R^)]

■^(Xj +x_Om) +(Уу +У₀ ~^прд) ^Rp

хехрНЦ/Су+х„5^+^

V(A^+x_Om) ⁺(У/⁺Уо ^— h_nPM) +(R_m-R_H)

VC^Y/ ^+X0m)" +(У/ ⁺Уо ~^црдУ +Rh

^(x^x^) +(У/+У₀ h_npM) +(R,„ R,/)

где 21 и 2J – максимальные значения индексов суммирования i и j.

В последнем выражении необходимо задание функции пропускания Pnp(iJ) объекта в конечном количестве точек, что и равносильно представлению сложного объекта набором излучателей Гюйгенса с известными координатами. При этом функция пропускания Pnp(Y y) трансформируется в матрицу, каждый элемент которой Pnp(iJ) равен единице или нулю, в зависимости от того, располагается ли этот элемент в проекции ОСФ или нет, а также прозрачен или нет объект для ЭМ-поля. Для уменьшения объема вычислений при расчете комплексной амплитуды непрозрачного для ЭМ-поля ОСФ целесообразно использовать принцип Бабине [1].

На рис. 2а приведена линия уровня матрицы PnP(iJ) = const , используемого в расчетах ОСФ, а на рис. 2б – результат расчета его двумерной дифракционной картины (график |O(m,n)| ).

Для задания формы ОСФ использовалась матрица из 20 строк (21 = 20) и 100 столбцов (2J = 100). Значения Ax и Ay при расчете по формуле (4) равнялись 0,2 м; поэтому размеры прямоугольной области рис. 2а составляют 4x20м при близких к этим цифрам габаритах ОСФ. Значения остальных величин: Ax₀ = Ah_npM =0,1m; 2M = 2N = 200; R_m = 10000m; R_h = 9750m. Отметим, что приведенная на рис. 2б двумерная дифракционная картина ОСФ для улучшения ее восприятия рассчитана при отличных от приведенных параметрах M,N, Ax₀ и Ah_np_M.

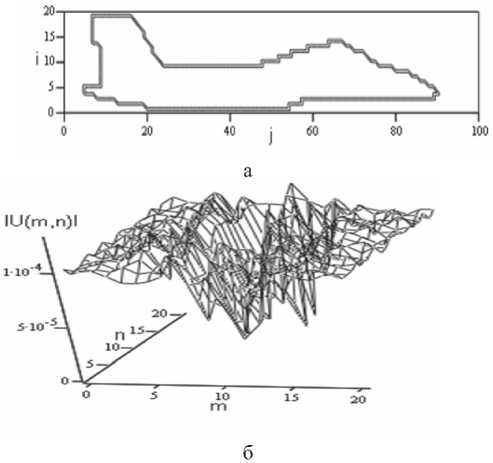
Рис. 2. Линия уровня матрицы Pnp(i,j) ОСФ(а) и двумерная дифракционная картина объекта (б)

Проверку качества расчетов можно осуществить путем восстановления функции пропускания РПр(х,у) ОСФ по его дифракционной картине с последующим формирования контура теневого радиоизображения объекта, предложенного в работе [4]:

1 2М 2N ,

Pnp(^Xi , У,) ~ — УУЦ^пЛпРм) ^Х m=0n=0

х expl/^W^^

VowJ2^2^ xexpH^+xj4(^^+h^j4 з/о^+^оЗ”^(у^~^пр^^

^+ХОт)2+У/+КН

~,     ,   ^"^  , _?Ж_РА .

•\/(^Xi^+X0m) ⁺(yj ^— hn_PM+h_npM) +(1^-^)

Сформированное по результату восстановления функции пропускания ОСФ теневое радиоизображение (как линия уровня 0пр(Х1>У,) = const) объекта приведено на рис. 3. Сравнение его с исходной проекцией (см. рис. 2а) позволяет сделать вывод о достаточно хорошем качестве восстановления функции пропускания и полученного радиоизображения ОСФ. Таким образом, предложенная методика расчета комплексной амплитуды ЭМ-поля ОСФ позволяет получить дифракционная картину, достаточно качественную для восстановления по ней функции пропускания и получения двумерного теневого радиоизображения объекта.

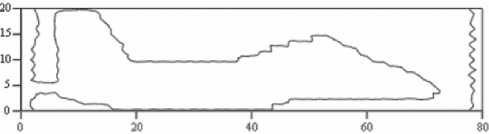
Рис. 3. Линия уровня результата восстановления функции пропускания ОСФ