Математическое моделирование процессов теплообмена для воздушных надувных коллекторов цилиндрической формы

1,2 Institute of Service and Business (DSTU branch), Shakhty, Russian Federation

Введение. Популяризация применения альтернативных источников энергии требует детального изучения новых гелиотехнических решений. Тем более, если речь идет о малоизученном сегменте надувных воздушных коллекторов (далее коллектор). Сложность и многофакторность процессов теплообмена в рассматриваемых системах определяют трудоёмкость сбора и анализа экспериментальных данных [1–8]. На этапе разработки новых устройств, а также оптимизации действующей модели коллектора, важна аналитика по каждому фактору, влияющему на эффективность устройства в целом. Разработанная математическая модель позволит изучить температурное поле коллектора в зависимости от направления потока солнечной радиации.

Постановка задачи. В качестве объекта исследования был выбран коллектор, представляющий собой систему последовательно соединенных замкнутых цилиндров, наполненных воздухом. Каждый цилиндр системы состоит из двух слоев: верхнего — светопропускающего и нижнего — теплопоглощающего (абсорбера). Касательно к выступающим точкам теплопоглощающей части цилиндра прикреплена теплоизоляционная подложка. В образовавшемся зазоре локализуется теплоноситель — воздух. Предлагаемая конструкция коллектора (рис. 1) позволяет обеспечить стабильно высокую температуру теплоносителя вне зависимости от направления потока солнечной радиации на поверхность коллектора.

Результаты натурных и лабораторных экспериментов [9] определили основные требования, предъявляемые к материалам коллектора. Для изготовления светопропускающего слоя коллектора был выбран полиэтилентерефталат. Данный материал обладает высокими показателями теплостойкости, стойкости к УФ-старению, а также коэффициентом светопропускаемости равным 0,85. Теплопоглощающий слой выполнен из шерстяного полотна, оно вкладывается по контуру нижнего полуцилиндра.

Рассмотрим процесс теплообмена в одном звене солнечного коллектора (рис. 2) в зависимости от направления потока радиации на поверхность коллектора. Ввиду наличия прозрачного верхнего слоя предложено допущение, что верхний слой не оказывает значительного воздействия на распределение температурного поля цилиндрического сегмента.

1        2

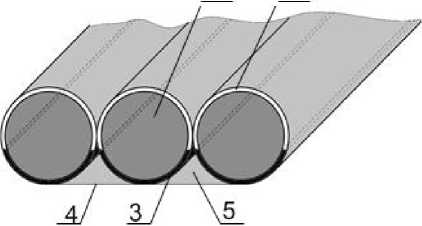
Рис. 1. Изображение воздушного надувного коллектора в разрезе:

1 — цилиндрический сегмент коллектора; 2 — светопропускающий прозрачный слой сегмента;

3 — теплопоглощающий слой сегмента;

4 — теплоизоляционный слой, 5 — область локализации теплоносителя

Fig. 1. Profile of air-inflatable collector:

1 - cylindrical collector segment; 2 - translucent transparent segment layer;

3 - heat-absorbing segment layer; 4 - heat-insulating layer,

5 - heat carrier localization area

Машиностроение и машиноведение

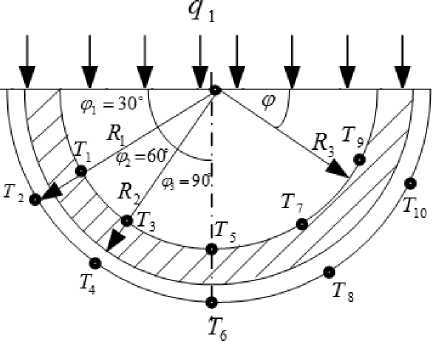
Рис. 2. Область расчета цилиндрического сегмента коллектора, в случае, если источник света расположен под прямым углом к диаметру сегмента коллектора

Fig. 2. Calculation domain of cylindrical collector segment in case when light source is normal to diameter of collector segment

Математическая модель задачи имеет вид:

область D 1

область D ₂

div ( х , gradT ^{( 1 )}) = 0 ;

div ( х ₂ gradT ^{( 2 )}) = 0.

Примем следующие граничные условия Р = R , ,

5 Т(2)

Х₂----- др

—

■ a , [ t ^{( 2 )} ( Я , , ф ) — Т окр ] ;

Р= R 2 ,

Т ( 1 )                ( 2 )                  ^{д Т} - 7   ^{д Т (2 )} ■

^{T  (} R 2 , ^ф , t ) ^{T (} R 2 , ^ф , t ) ; ^Х1 ~ ^Х 2 -ч ;

др      др р = Rз.

Для расчета температурного поля будем использовать метод конечных элементов (МКЭ). На рис. 3 представлена конечно-элементная сетка, покрывающая область расчета.

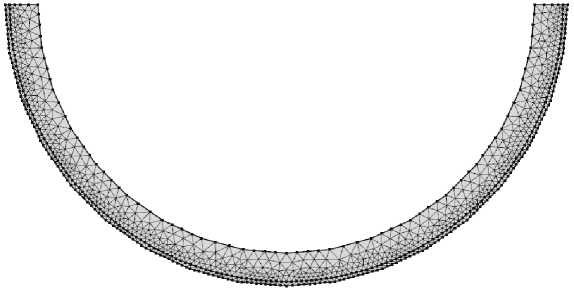
Рис. 3. Конечно-элементная сетка области расчета

Fig. 3. Finite-element grid of calculation domain

Решение данной задачи сводится к итерационному численному решению прямых задач и минимизации функционала

N

J = Е ( T j — Т и^{з м} ) , j = 1^х

где N — число точек измерения температуры Т*1”, Tj — значения температуры в тех же точках, полученных путем решения прямых задач методом конечных элементов.

МКЭ в настоящее время стал одним из самых распространенных и эффективных методов решения задач математической физики и техники, сформулированных в виде краевых задач для дифференциальных уравнений с частными производными.

Пусть требуется найти распределение температуры T(N) в некоторой области V, удовлетворяющей уравнению стационарной теплопроводности div (х( N) gradT (N)) + f (N) = 0                                      (4)

и условию на поверхности S , ограничивающей область V ,

хд_ ( M ) = _а( M ) T ( M ),                                 (5)

где Х ( N ) — коэффициент теплопроводности, в общем случае функция точки N е V ; а ( M ) — коэффициент теплоотдачи, M е S ; f ( N ) — объемная плотность источников тепла.

Первый этап МКЭ — построение неортогональной сетки, покрывающей область расчета V . Сетка образует совокупность конечных элементов, например, тетраэдров, в плоскопараллельном поле треугольников. Далее следует нумерация элементов и узлов, составление массивов координат узлов.

На втором этапе выполняется аппроксимация искомых и известных функций (в нашем случае T ( N) и f ( N ) ). На третьем этапе будет показано, что математическую модель исходной задачи можно преобразовать так, что аппроксимацию функций T ( N) и f ( N ) допустимо искать в пространстве дифференцируемых функций

C .

Построим в этом пространстве подпространство с конечным

базисом { у j }.   . Базисные функции у j ( N )

выберем финитными (с конечным носителем) и кусочно-линейными.

В j -м узле сетки положим у j = 1, в остальных узлах у j = 0 .

Тогда аппроксимирующие функции на втором этапе МКЭ будут иметь вид

T ( x , y , z ) = L T у j ( x , y , z ) ; f ( x , y , z ) = 1, ^fj У j ( x , У , z ) , j = 1                                               j = 1

где n — количество узлов сетки; T j = T ( x j , y j , z j ) ; f j = f ( x j , y j , z j ) .

В пределах k -го конечного элемента искомая функция представляется в виде

~           \     m + ⁴

T (x, y, z )= L Tj у j (x, y, z), j=m+1

где у j = a^k j x + b^ky + c j z + d j .

В случае плоскопараллельного поля имеем

T ( X , y ) = m L jj ( x , y ) , j = m + 1

kk k k где у j = a j x + b j y + c j .

Постоянные коэффициенты у j определяются через координаты узлов элемента.

На третьем этапе интегралы по области V заменяются суммой интегралов по конечным элементам V ^k , интегралы по S — суммой интегралов по граням элементов, аппроксимирующих S .

Строится система уравнений МКЭ и учитываются граничные условия. Эту систему называют дискретной математической моделью задачи (ДММ).

Рассмотрим построение ДММ для проекционного варианта МКЭ, суть которого заключается в минимизации нормы невязки

£ = dzvXgradT ( N) + f путем ортогонального проектирования ее на конечномерное подпространство с базисом

{у j } . ₁ . Минимум

невязки обеспечен в том случае, если все скалярные произведения невязки £ и у j будут равны нулю.

В МКЭ принято использовать скалярные произведения более широкого класса функций ( L ₂).

В результате получим систему МКЭ в виде

Машиностроение и машиноведение

JJJу i [ div ( X gradT ) + f J dV = 0, i = 1,2,..., n .

Используя известные тождества div (фа ) = фdivа + agradф ;

JJJ div ( ф а ) dV = JJ ф a_ndS ,

VS где ф — скалярная функция; a — векторная функция; an — проекция а на внешнюю по отношению к V нормаль, получим систему уравнений вида

JJJXgradTgradуidV = JJХуi — dS + JJJуifdV , i = 1,2,...,n,(7)

v                      s     dn где n — число узлов сетки, в которых неизвестны Tj.

Дальнейшие преобразования (7) приводят к системе уравнений вида

XXkXPT = XXkqkJJykdS + XXfjJJJykykkdV, i = 1,2,...,n,(8)

k j          k       Skkj Vk к  d T где    q = —

О n S^k

нормальная     производная

T ( M )       на     грани       S^k e S

к -го конечного элемента (принимается постоянной); V^k — область к -го элемента; p j = JJ grad у ^к grad у ^dV .

Vk

Внешнее суммирование в (8) (по k ) ведется по всем элементам, имеющим общий узел i , внутреннее (по j ) — по всем узлам k -го элемента. Для всех внутренних узлов первый интеграл в правой части (8) равен нулю.

Систему (8) называют дискретной математической моделью задачи, если в нее подставить граничные условия. Решение системы (8) и использование (6) позволяют определить все интересующие величины (градиенты, потоки и т.п.).

Исходные данные: температура окружающего воздуха TOK= 23 °С; тепловой поток q = q1 sinф, q1 = 310 Вт/м2 (значение теплового потока от источника излучения). Теплопроводность: светопропускающего слоя Х1 = 0,03 Вт/м-К;   теплопоглощающего слоя   X2 = 0,34 Вт/м-К;   коэффициент теплоотдачи aT = 9,5 Вт/м2-К; R1 = 0,05 м; R2 = 0,0492 м; R3 = 0,0442 м; ф1 = 3 0°; ф2 = 60°; ф3 = 90°.

Необходимо определить распределение температур в установившемся режиме в точках: T 1 ( R ₃, ф 1 ) ;

T 2 ( R „ф , ) ; 7 3 ( R 3 , ф 2 ) ; T 4 ( R „ф ₂ ) ; T ₅ ( R 3 , ф 3 ) ; T ₆ ( R „ф 3 ) .

Результаты вычислительного эксперимента приведены в таблице1.

Таблица 1

Table 1

T1 (R3, ф1) T2 (R1, ф1) T3 (R3, ф2) T4 (R1, ф2) T5 (R3, ф3) T6 (R1, ф3) Вычисленные значения, °С 48,7 41,3 56,7 46,8 60,1 49,2

Далее приведены результаты математического моделирования теплообмена в одном сегменте коллектора для случая, когда источник света расположен под углом 45° к диаметру образца (рис. 4).

Исходные данные соответствуют тем, которые использовались при моделировании первого случая. Найдем распределение температур в установившемся режиме в точках: T 1 ( R 3 , ф 1 ) ; T ₂ ( R 1 , ф 1 ) ; T ₃ ( R ₃, ф ₂ ) ; T 4 ( R 1 , ф 2 ) ; T 5 ( R 3 , ф ₃ ) ; T 6 ( R 1 , ф ₃ ) ; T 7 ( R ₃, ф 4 ) ; T ₈ ( R „ф 4 ) ; T 9 ( R ₃, ф 5 ) ; T ₁₀ ( R_v ф 5 ) .

Y , °	0–10	10–20	20–30	30–60	60–70	70–80	80–90	90–100	100–110	110–120	120–130	130–180
q , Вт/м 2	182	194	202	210	202	194	182	126	122	117	111	105

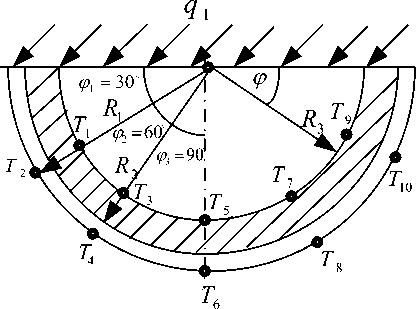
Рис. 4. Область расчета для случая, когда поток солнечного излучения расположен под углом к диаметру сегмента коллектора

Fig. 4. Calculation domain for case when solar radiation flux is set at 45° angle to collector segment diameter

Значения плотности теплового потока, приведенные в таблице 2, найдены на основе решения обратной задачи теплообмена.

Таблица 2

Table 2

Адекватность математической модели была проверена экспериментально. С этой целью был изготовлен замкнутый цилиндрический сегмент коллектора. В качестве абсорбера использовалось шерстяное полотно. В ходе эксперимента образец воздушного коллектора был установлен вертикально. Напротив образца на расстоянии 0,8 м располагался источник света — прожектор с галогеновой лампой мощностью 1кВт. Излучение на поверхность теплопоглощающего слоя было направлено под углом 45°. С помощью датчиков температуры ИВТ (прибора для измерения плотности теплового потока) были зафиксированы значения температуры наружной поверхности светопропускающего и теплопоглощающего слоев в период термостабилизации, т.е. по истечении 20 мин. воздействия на коллектор источника света.

Результаты измерительного и вычислительного экспериментов приведены в таблице 3.

Таблица 3 Table 3
	T ( R 3 , Ф 1 )	T ( R 1 , Ф 1 )	T 3 ( R 3 , Ф 2 )	T 4 ( R 1 , Ф 2 )	T 5 ( R 3 , Ф з )
Измеренные значения, ° С	47,0	39,0	48,0	36,0	35,6
Вычисленные значения, ° С	46,1	38,2	44,0	36,7	38,8
Погрешность, %	1,9	2,1	8,3	–1,9	–8,2
	T 6 ( R 1 , Ф з )	T 7 ( R 3 , Ф 4 )	T 8 ( R 1 , Ф 4 )	T 9 ( R 3 , Ф 5 )	T 10 ( R 1 , Ф 5 )
Измеренные значения, ° С	30,6	33,0	30,0	33,4	32,3
Вычисленные значения, ° С	33,1	34,5	30,0	34,4	30,0
Погрешность, %	–8,2	–4,5	0,0	–3,0	7,1
10              2 ^ ( T - Г ') Среднеквадратическая погрешность А ( T ) = м———--- = 2,08 ° С.

Следовательно, результаты моделирования процессов теплообмена в сегменте коллектора для разных направлений воздействия потока солнечного излучения согласуются с результатами измерений с достаточной для инженерных задач точностью.

Машиностроение и машиноведение

Выводы. Прирост температуры теплопоглощающего слоя по отношению к температуре окружающей среды составил от 7° до 26,2° в зависимости от рассматриваемой части сегмента коллектора и направления воздействия потока солнечной радиации. Таким образом, локализуясь между теплопоглощающим слоем и теплоизоляционной подложкой, конструкция коллектора обеспечит нагрев теплоносителя. Максимальные значения температурного поля поверхности теплопоглощающего слоя (60°) коллектора отмечаются при прямом воздействии солнечного излучения. Изменение угла воздействия потока излучения до 45° приводит к снижению температуры. В зависимости от сектора воздействия, температура поверхности теплопоглощающего слоя может снижаться на 3-14° по отношению к замерам при прямом воздействии солнечных лучей.

Адекватность разработанной математической модели позволит разработать программный продукт, который автоматизирует процесс расчета температурного поля коллектора.

• 1.    ГОСТ 28205-89. Основные методы испытаний на воздействие внешних факторов. Часть 2. Испытания. Руководство по испытанию на воздействие солнечной радиации / Государственный комитет СССР по стандартам. — Москва : Издательство стандартов, 1989г. — 17с.

• 2.    ГОСТ Р 51910-2002. Методика исследования и проверки ускоренными методами влияния внешних воздействующих факторов на долговечность и сохраняемость технических изделий / Государственный комитет стандартов Российской Федерации, 2002г. — 20с.

• 3.    ГОСТ Р 26883-86. Внешние воздействующие факторы. Термины и определения / Государственный комитет СССР по стандартам — Москва : Издательство стандартов, 1986г. — 9с.

• 4.    ГОСТ 28202-89 (СТ МЭК 68-2-5-75). Основные методы испытаний на воздействие внешних факторов. Часть 2. Испытания. Имитированная солнечная радиация на уровне земной поверхности: / Государственный комитет СССР по стандартам — Москва : Издательство стандартов, 1989. — 5.

• 5. ГОСТ Р 55617.1-2013. Возобновляемая энергетика. Установки солнечные термические и их компоненты. Солнечные коллекторы. Часть 1. Общие требования / Государственный комитет стандартов Российской Федерации, 2013г. — 5с.

• 6.    ГОСТ Р 51595-2000. Нетрадиционная энергетика. Солнечная энергетика. Коллекторы солнечные. Общие технические условия / Государственный комитет стандартов Российской Федерации, 2001г. — 27с.

• 7.    ГОСТ Р 55617.2-2013. Возобновляемая энергетика. Установки солнечные термические и их компоненты. Солнечные коллекторы. Часть 2. Методы испытаний / Государственный комитет стандартов Российской Федерации, 2014г. — 94с.

• 8.    Смирнова, О. А. Концепция комплексной оценки эксплуатационных показателей надувного коллектора / О. А. Смирнова, М. А. Гончарова, Ю. Э. Аветисян // Инновационные исследования: проблемы внедрения результатов и направления развития. — 2017. — №2. — С.63-67.

• 9.    Смирнова, О. А. Конфекционирование полимерных материалов для надувных воздушных солнечных коллекторов / О. А. Смирнова И. В. Ващинская, М. А. Гончарова, Ю. Э. Аветисян // Инновации в науке. — 2016. — №4 — С.52-57.

• 10.    Бахвалов, Ю. А. Обратные задачи электротехники: монография / Ю. А. Бахвалов, Н. И. Горбатенко, В. В. Гречихин — Новочеркасск: Изд-во журнала «Изв. ВУЗов. Электромеханика», 2014. — 211 с.

• 11.    Никифоров, А. Н. Методы оптимизации: учеб. пособие / А. Н. Никифоров — Новочеркасск : ЮРГТУ (НПИ), 2007. — 160 с.