Математическое моделирование прочности шпилечного соединения сборных плит кристаллизатора МНЛЗ

При разливке стали в МНЛЗ наиболее ответственным узлом, определяющим ее технико-экономические показатели, является кристаллизатор. Наиболее распространенными являются конструкции кристаллизаторов со сверленными цилиндрическими или фрезерованными щелевыми каналами в медной стенке [1, 2].

Из-за необходимости сверлить длинные отверстия кристаллизаторы первой конструкции сложны в своем изготовлении, кроме то- го, довольно трудоемка технология очистки каналов от накипи, проводимая во время ремонта стенок кристаллизатора [3].

В настоящее время перспективными являются более простые в эксплуатации и изготовлении составные кристаллизаторы, состоящие из медной рабочей стенки со щелевыми каналами и стального внешнего корпуса. В них охлаждающая вода подается снизу, проходит через прямоугольные вертикальные каналы, далее собирается в коллекторе сверху и отводится из кристаллизатора.

При всех явных преимуществах перехода от цилиндрических каналов к щелевым возникают и проблемы, в частности, связанные с простым и надежным закреплением медной и стальной плит. При номинальном давлении воды в каналах P в = 6 бар на медные плиты действует существенная сила давления, кроме того, на медную стенку действуют переменные сдвиговые силы, связанные с протяжкой слитка, и динамические усилия от механизма качания.

Во всех известных промышленных конструкциях составных кристаллизаторов соединение медной и стальной плит осуществляется посредством множества стальных шпилек, причем они расположены по поверхности плиты крайне неравномерно. Возможные места их расположения ограничены наличием каналов охлаждения, шпонок и уплотнителя. Таким образом, при закреплении плит посредством резьбовых соединений возникает задача расчета прочности шпилечного соединения при всей совокупности действия максимальных сил и существующей неравномерности нагружения шпилек.

Постановка задачи

На металлургических предприятиях в России и за рубежом происходит переход от кристаллизаторов МНЛЗ со сверлеными каналами к сборным кристаллизаторам. На рис. 1 показан схематический чертеж широкой медной стенки кристаллизатора слябовой МНЛЗ, приведено расположение щелевых каналов и соединительных шпилек. Основные геометрические характеристики медной стенки приведены в табл. 1.

Для соединения медной плиты и стального кожуха используется шпилечное соединение, показанное на рис. 2. Оно включает в себя шпильку, втулку с наружной резьбой М30 х 1,5, шайбу и гайку. Основные геометрические параметры резьбового соединения показаны в табл. 2. В качестве крепежного соединения стальной и медной плит используются шпильки М20 х 100 ГОСТ 9066-75 (58 – класс прочности, материал шпильки – сталь 20).

Целью работы является создание математической модели для определения коэффициента неравномерности нагружения шпилек и

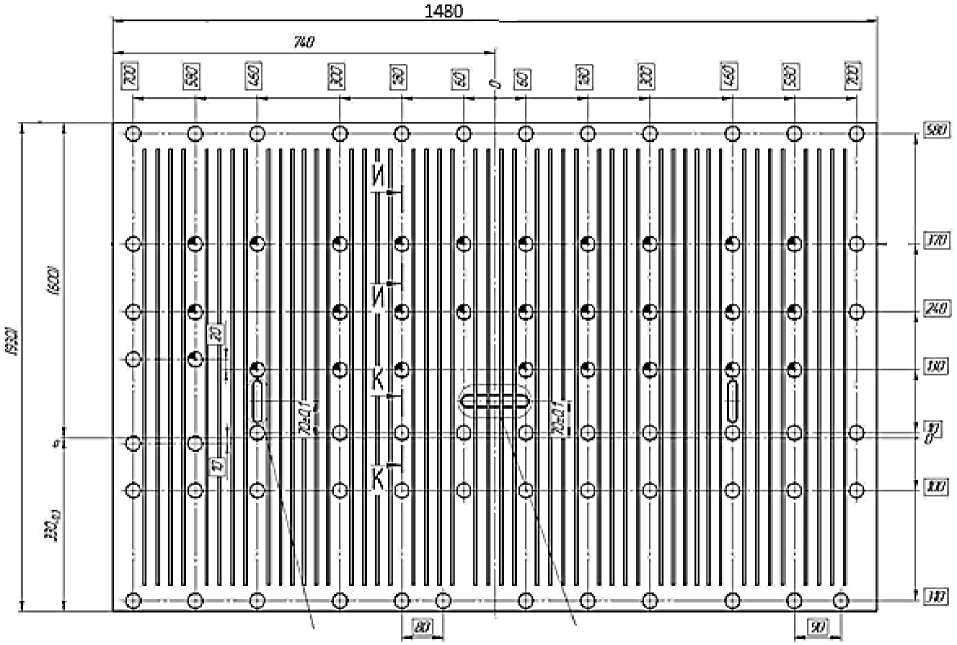
Рис. 1. Расположение щелевых каналов, соединительных шпилек в широкой медной стенке кристаллизатора

Таблица 1

Геометрические характеристики медной стенки кристаллизатора со щелевыми каналами

Название параметра	Обозначение	Единица измерения	Численное значение
Длина стенки кристаллизатора	L	мм	1480
Длина малой стенки кристаллизатора	L м	мм	250
Высота стенки кристаллизатора	B	мм	930
Число соединительных шпилек	n шп		81
Ширина вертикальных каналов	h вк	мм	5
Число вертикальных каналов	n вк		48
Длина вертикальных каналов	L вк	мм	830
Ширина горизонтальных водяных каналов	h гк	мм	60
Число горизонтальных каналов	n гк		2
Длина горизонтальных каналов	L гк	мм	1380
Число шпонок 16 х 10 х 80	n шп1		2
Число шпонок 22 х 14 х 130	n шп2		1

Таблица 2

Параметры используемого резьбового шпилечного соединения

Название параметра	Обозначение	Единица измерения	Численное значение
Диаметр шпилек	d	мм	20
Средний диаметр резьбы	d 2	мм	18,376
Внутренний диаметр резьбы	d 1	мм	16,933
Шаг резьбы	P	мм	2,5
Число заходов резьбы	n ш		1
Наружный диаметр опорной поверхности гайки	D ш0	мм	37
Диаметр втулки М30 х 1,5 в медном корпусе	d ш0	мм	30
Угол профиля, равный углу между смежными сторонами	а	град	60
Угол подъема винтовой линии	f Pn ) Y = arctg ш 1 V П d 2 )	град	2,48
Длина резьбы со стороны втулки	l рез	мм	23,5

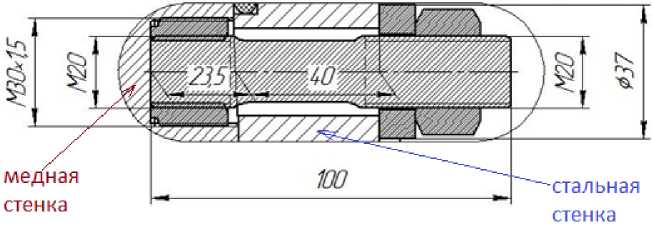
Рис. 2. Основные геометрические размеры шпилечного соединения медной плиты и стального кожуха кристаллизатора

запаса прочности соединения медной и стальной плит для заданной конструкции сборного кристаллизатора МНЛЗ и выбранных параметров шпилечного соединения.

Определение коэффициента неравномерности нагружения шпилек

Из размеров, приведенных на чертеже (см. рис. 1), определяем площади:

медной плиты

S _п = L ■ B « 1,376 м 2 ;

смоченной поверхности водой со стороны стальной плиты

S = n h L + n h L ~ 0,365 м. в вк вк вк гк гк гк

Вычисляем площадь, занимаемую шпонками:

A S = n _шп1 ( 16 ■ 80 ) + n _шп2 ( 22 - 130 ) » 0,005 м 2 , и площадь, занимаемую отверстиями под шпильки:

S ш = n шп ■ d 20 ’V4 « 0,057 м².

Исходя из полученных значений, можно получить площадь соприкосновения медной и стальной поверхностей

SCT = Sn -SB -AS -Sm «0,949 м2 ст п в          ш и определить силу нормального давления со стороны воды на стальную плиту как

F h = S в ■ Р в ~ 22,3 тс.

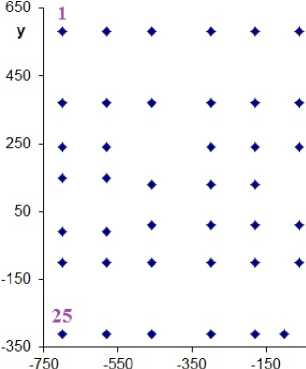
Для установления величины коэффициента неравномерности нагружения шпилек была выбрана система декартовых координат. Ее начало находится на пересечении вертикальной линии, проходящей через середину медной плиты L /2 и горизонтальной линии – на расстоянии 330 мм от нижнего ее края (рис. 3). Из рис. 1 и 3 видно, что для рассматриваемой конструкции медной стенки шпиль-

ки по поверхности плиты расположены неравномерно. Учет возникающих неодинаковых нагрузок на шпильки осуществлялся с помощью расчета коэффициента неравномерности K ₀ . Считали, что максимальная растягивающая сила, приходящаяся на одну шпильку, пропорциональна этому коэффициенту и средней растягивающей силе:

F = K 0 ■ F ,                           (1)

где F = F _h/ n _шп « 2702 Н » 0,28 тс.

Задаем положение шпилек, расположенных на плите ( x_i , y_i ) относительно выбранной системы координат (см. рис. 3). Расстояние от i до j шпильки можно определить как евклидовую норму:

r i , j = V⁽ x i ^- x j ^{)2 + (} y i ^- y j ⁾² .              ⁽²⁾

Полученная матрица r симметрична относительно нулевой главной диагонали: r i j = r j i , Г i = 0.

Для i шпильки можно выделить кластер, включающий в себя k ближайших к ней шпилек. Для этого проводится сортировка r _{i , j} , в результате чего для i шпильки получим вектор расстояний k ближайших ее соседей ^Si , k = ( ^Si ,1 , ^Si ,2 , - , ^Si , k ) . Можно определить среднее расстояние в кластере для i шпильки 1 ^k

S =— ^Sy , среднее значение расстояния по i kj=1 i всем кластерам S = — У Si «188 мм и да-nшп i=1

лее относительное расстояние для кластера, связанного с i шпилькой как е i = S i / S .

• ♦   ♦   ♦     ♦   ♦   > 1-->12

• ♦   ♦   ♦    ♦   ♦   ♦ 13 >24

• ♦   ♦   ♦    ♦   ♦   ♦ 71 >81

• ♦   ♦   ♦    +   +     61->70

• ♦   ♦   ♦    *   *   * 49-60

• ♦   ♦   ♦     *   *   * 37-->48

• ♦   ♦   ♦     ♦   ♦ ♦ 25->36

50      250      450      650 х

Рис. 3. Расположение шпилек и их нумерация по медной стенке кристаллизатора

а)                                                                б)

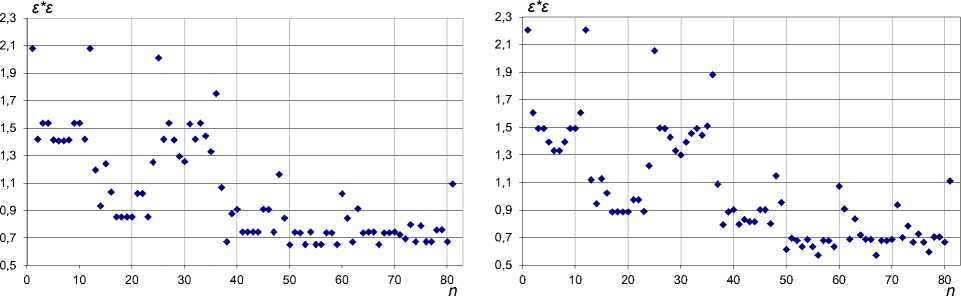
Рис. 4. Расчетный коэффициент неравномерности расположения шпилек от их номера, показанного на рис. 3, при разном количестве шпилек, входящих в кластер: а – k = 5; б – k = 8

Нагрузка на резьбовое соединение пропорциональна площади соединяемых плит, которые удерживает шпилька, поэтому будем полагать, что коэффициент неравномерности нагрузок для i шпильки пропорционален квадрату относительного расстояния для кластера:

K 0 i ~ ε i ² . (3)

Значения εi2 для всех шпилек (nшп = 81) при k = 5 и k = 8 показаны на рис. 4. Видно, что максимальное значение имеют четыре точки. По номерам этих точек (1, 12, 25 и 36) можно установить, что они лежат вблизи углов прямоугольной плиты. Из-за особенностей данного расположения на самом деле нагрузка на эти шпильки существенно меньше. Несколько точек, например 3, 4, 9, 10, имеют значение εi2 чуть больше 1,5, но они также располагаются вблизи края пластины. Примерно 25 % шпилек имеют 1 < εi2 ≤ 1,5, исходя из этого для рассматриваемой конструкции расположения шпилек коэффициент их нерав- номерности по нагрузке с запасом можно считать равным K0 ≈ 1,5.

Математическая модель для определения прочности шпилечного соединения медной и стальной плит кристаллизатора

Основные механические характеристики материалов и технологические параметры сведены в табл. 3.

Предварительная затяжка болта при сборке должна обеспечить плотность соединения и отсутствие раскрытия стыка после приложения силы давления воды F _н = S _в ⋅ P _в во время работы кристаллизатора.

В работе [6] принимается, что при установке шпилек в отверстие с зазором внешняя растягивающая сила полностью передается болту. От этой силы болт удлиняется на ∆ l _б . На это же значение уменьшается сжатие деталей, и нагрузка на болт со стороны плиты понижается. Допустимый зазор между стянутыми стенками не более 0,15 мм.

Таблица 3

Механические характеристики материалов и технологические параметры работы кристаллизатора

Название параметра	Обозначение	Численное значение	Единица измерения
Номинальное давление в водяной системе	P в	6	ати
Максимальное испытательное давление в водяной системе	р , в мах	12	ати
Максимально допустимая сила отрыва слитка [4]	F s mах	20	тс
Коэффициент трения сталь-сталь [5]	f	0,15
Коэффициент трения сталь-медь [5]	f м	0,2

Внешнее усилие F _н перераспределяется

между стыком и винтом, причем одна часть внешней нагрузки дополнительно нагружает винт, а другая идет на уменьшение затяжки стыка [7]. Весь стык ослабляется на величину k F = ( 1 -/ ) • F _H, а каждая i шпилька - k F i = ( 1 — / ) • F i , где X — коэффициент основной нагрузки, равный 0,25.

Кроме нормальной силы F _н на плиту действует усилие сдвига F_s , направленное

приведенный угол трения. Величина эквивалентного напряжения, возникающего в стерж-

не, равна

4 • ^max ( ^F 0 , ^F ис_n )

° e = Кэ-------- п^ d1

где коэффициент пропорциональности

^К э =

1 + 12

d 22 ( tg ² ( Y + Р’ ) )

d 1²

.

вертикально вдоль поверхности кристаллизатора. Усилие сдвига можно определить, зная максимально допустимую силу отрыва слитка от кристаллизатора:

smax s = 2•(L + Lм).

В работе [7] указывается, что если гайка изготовлена из менее прочного материала, чем болт, то, несмотря на большую площадь среза ее витков, они могут оказаться менее прочными, чем витки резьбы болта. В этом случае в выражении (8) вместо внутреннего диаметра резьбы d ₁ подставляется диаметр

Первоначальная сила затяжки шпильки с учетом сдвигающей силы при х = 0,25

втулки d _ш0 , а в условии прочности берутся

свойства менее прочного материала, в данном

случае меди:

F = - F 0- + ( 1 — х^ F , n шп

4max( F ₀ , F _0исп ) k э          2

^{п d} ш0

где F 0 = F s • S s/ f м - условие несдвигаемости медной и стальной плит за счет сил трения, при этом коэффициент запаса по сдвигу принимался S s = 1,2 . При расчете полагали, что F i = F 1 .

Сила затяжки при испытательном давлении воды Р = Р втах

77     _ S в • Р в max ^{(1 — х )}                     /т-х

F 0исп =                     .                    ⁽⁶⁾

n _шп

Давление, стягивающее плиты во время работы кристаллизатора, p о = F^jS _ст.

Условие прочности болтового соедине- ния: °e <°r, отсюда коэффициент запаса s прочности s = °r.                                (10)

° e

Желательно, чтобы длина резьбы в медьсодержащей стенке составляла H = 1,5· d = 30 мм . В рассматриваемом случае она равняется 22,5 мм.

Момент затяжки T _з связан с усилием затяжки F ₀ следующими зависимостями [6]:

T 3 = l з • max ( F 0 , F ) _m n ) ,

где

l з =

ytg ( У + Р ‘ )

₊ f • D Шо

3 D ш² 0

^d ш0

^d ш0

ко-

эффициент пропорциональности момента за-

f тяжки от усилия затяжки; р = arctg----м—- cos(а/2)

–

Результаты моделирования запаса прочности соединения медной и стальной стенки

Пределы прочности и текучести для применяемых медных сплавов для изготовления кристаллизаторов, которые используются при изготовлении сборных стенок, приведены в табл. 4 [8].

Зная предел прочности ° _в, можно для медьсодержащих сплавов найти напряжение

Таблица 4

Предел прочности ° _в для некоторых медных сплавов, Н/мм²

Температура, °С	M2	M	MC	МЦ	НМС
20	230	220	440	230	750
100	225	–	–	–	–
200	211	–	–	–	–
300	198	150	310	–	650

Таблица 5

Результаты компьютерного расчета шпилечного соединения медной и стальной плиты

Название параметра Обозначение Численное значение Единица измерения Численное значение Единица измерения Сила нормального давления со стороны воды на стальную плиту Fн 218 880 Н 22,3 тс Средняя растягивающая сила на одну шпильку с учетом K0 F1 4053 Н 0,41 тс Усилие сдвига плиты Fs 83 838 Н 8,55 тс Условие несдвигаемости плиты F 503 029 Н 51,3 тс Средняя сила затяжки шпильки F0 9250 Н 0,94 тс Сила затяжки, связанная с испытанием при повышенном давлении воды Pмах Fa 0 исп 4053 Н 0,41 тс Средний коэффициент соотношения площадей каналов и шпилек К i ср 6,4 – – Давление, стягивающее плиты при работе кристаллизатора p0 530 104 Па 5,3 ати Приведенный угол трения ρ' 0,227 рад 13,0 град Коэффициент пропорциональности момента затяжки от усилия затяжки lз 0,0051 м 5,1 мм Момент затяжки Tз 46,9 Н м – – Коэффициент для эквивалентного напряжения kэ 1,44 – – Величина эквивалентного напряжения в шпильке σe 59 МПа 59 Н/мм2 Величина эквивалентного напряжения во втулке σe 19 МПа 19 Н/мм2 Запас прочности срыва шпильки по стали sст 6,74 – – Запас прочности срыва шпильки по меди sм 5,29 – – среза тср ~ 0,1-ств = (0,2-0,3)-стr и предел

текучести ст r

—

ст

в

[9]. Данные о пре-

делах прочности ст _вс = 500 МПа и текучести

ст r _с = 400 МПа для стали (сталь 20) были взяты из справочника [10].

По разработанной математической модели составлена компьютерная программа расчета « Рациональное расположение шпилек ». Она позволяет по известным геометрическим и технологическим параметрам определить коэффициент неравномерности нагружения K 0 , среднее напряжение, которое действует в каждой шпильке при их конкретном расположении по поверхности плиты, момент затяжки

шпилек и запас прочности на срез резьбы в медной стенке.

Проведен механический расчет шпилек, которые предполагается использовать для крепления медных плит кристаллизатора, характеристики которых приведены в табл. 2. Коэффициент неравномерности, исходя из приведенного анализа, задавался как K 0 = 1,5. Результаты компьютерного расчета при этом значении показаны в табл. 5.

Для выбранного значения предела прочности медной стенки ст _в = 220 МПа (соответственно ст r =100 МПа и т _ср = 25 МПа) получены: запас прочности для соединения медь-втулка s = 5,29, для стальной шпильки - s = 6,74, значение момента затяжки T з = 46,9 Н·м.

Результаты моделирования прочности шпилечного соединения при использовании шпилек с отверстием под термодатчик

Для контроля температуры при работе кристаллизатора в него устанавливаются термодатчики. На рис. 5 показан чертеж шпильки с отверстием под термодатчик.

Оценим, насколько технологическое отверстие снижает прочность шпилечного соединения. Максимальное отверстие внутри шпильки имеет диаметр dотв = 7 мм. Определим эквивалентный диаметр шпильки dэкв = Vd 2 — dо>тв =18,7 мм. Полученное значение несущественно отличается от диаметра шпильки d и не влияет на разрыв материала шпильки по сравнению с прочностью резьбы, то есть при этих условиях резьба остается лимитирующим фактором.

Созданная компьютерная программа позволяет анализировать надежность соединения при моделировании разных ситуациях, в том числе форс-мажорных и аварийных. Например, можно промоделировать уменьшение количество шпилек на 25 %, вместо n шп = 81 зададим n шп = 61. Полученные результаты расчета сведены в табл. 6.

Видно, что запас прочности уменьшился, он составляет по меди 5 ® 4, а момент затяжки шпилек увеличился: T _з = 62,2 Н∙м. Согласно общепринятым нормам в резьбовых соедине-

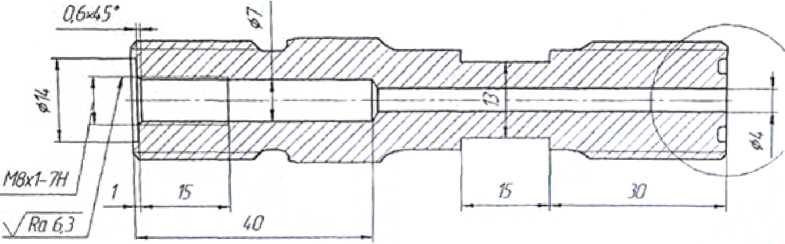
Рис. 5. Основные геометрические размеры шпильки с отверстием под термодатчик

Таблица 6

Результаты компьютерного расчета шпилечного соединения медной и стальной плиты

Название параметра	Обозначение	Численное значение	Единица измерения	Численное значение	Единица измерения
Сила нормального давления со стороны воды на стальную плиту	F н	218 880	Н	22,3	тс
Средняя растягивающая сила на одну шпильку с учетом K 0	F 1	5382	Н	0,55	тс
Усилие сдвига плиты	F s	83 838	Н	8,55	тс
Условие несдвигаемости плиты	F	503 029	Н	51,3	тс
Средняя сила затяжки шпильки	F 0	12 283	Н	1,25	тс
Сила затяжки, связанная с испытанием при повышенном давлении воды P max	0 исп	5382	Н	0,55	тс
Средний коэффициент соотношения площадей каналов и шпилек	К i ср	8,5		–	–
Давление, стягивающее плиты при работе кристаллизатора	p 0	522 323	Па	5,2	ати
Приведенный угол трения	ρ '	0,227	рад	13,0	град
Коэффициент пропорциональности момента затяжки от усилия затяжки	l з	0,0051	м	5,1	мм

Окончание табл. 6

Название параметра Обозначение Численное значение Единица измерения Численное значение Единица измерения Момент затяжки т з 62,2 Н м – – Коэффициент для эквивалентного напряжения kэ 1,44 – – Величина эквивалентного напряжения в шпильке σe 79 МПа 79 Н/мм2 Величина эквивалентного напряжения во втулке σe 25 МПа 25 Н/мм2 Запас прочности срыва шпильки по стали sст 5,08 – – Запас прочности срыва шпильки по меди sм 3,99 – – ниях для подобных конструкций при контроле затяжки шпилек запас прочности должен быть не менее s = 1,3-1,5, а при отсутствии контроля - s = 1,5-2,5 [6].

Полученные результаты говорят о том, что даже если по всей площади плиты будут отсутствовать (или нарушится затяжка) у 25 % шпилек, то соединение остается вполне надежным.

Выводы

• 1.    При заданном расположении шпилек по поверхности соединения медной и стальной плит предложена методика расчета коэффициента неравномерности нагружения шпилек. Показан пример расчета для предлагаемой конструкции широкой стенки промышленного сборного кристаллизатора.

• 2.    Показана математическая модель для расчета запаса прочности срыва шпильки. Для предлагаемой конструкции кристаллизатора получен запас прочности для соединения медь-втулка s = 5,29. Определен необходимый момент затяжки шпильки, обеспечивающий нераскрытие стыка, который составил около 47 Н·м. Запас прочности срыва шпильки и момент ее затяжки получены при максимальном испытательном давлении воды 12 ати и с учетом максимального внешнего усилия сдвига при трении слитка о стенку кристаллизатора, равного 20 тс.

• 3.    Создана компьютерная программа, позволяющая анализировать надежность соединения сборных стенок кристаллизатора при моделировании разных ситуаций, в том числе форс-мажорных и аварийных.