Математическое моделирование простой гидравлической системы

Моделирование гидравлических систем, является важной задачей в процессе наладки сложных трубопроводов, а также при нахождении путей эффективного управления данными системами [1].

Цель исследования – смоделировать гидравлическую систему.

В качестве объекта исследования выступает математическая модель системы.

Методика выполнения работы начинается с составления системы уравнений расходов потоков и давления в точках ветвления. Для решения данной системы использован метод математической декомпозиции, позволяющий существенно снизить размерность решаемой задачи и определять все искомые переменные путем решения системы уравнений значительно меньшей размерности, чем размерность исходной системы.

Для выбора алгоритма математической декомпозиции, который позволит определить искомые переменные, необходимо построить и проанализировать информационную матрицу системы уравнений.

Гидравлическая система – это совокупность элементов, воздействующих на текучую среду таким образом, что свойства каждого элемента оказывают влияние на состояние текучей среды во всех элементах системы [2].

Гидравлическая система представлена на рисунке 1.

Данные системы включают насосы, компрессоры и другие единицы оборудования. В них наряду с жидкостью могут перемещаться потоки газа, газо- и парожидкостной смеси.

баки аккумуляторы

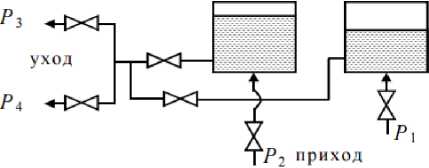
Рисунок 1 – Схематическое изображение гидравлической системы с двумя закрытыми емкостями (аккумуляторами)

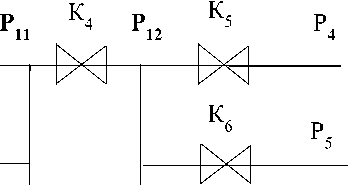
Схема моделируемой гидравлической системы, представлена на рисунке 2.

На данной схеме P 1 , Р 2 , Р 3 – давления на входах; P 4 , Р 5 , Р 6 – давления на выходах, Р₁₁ и Р₁₂ – точки ветвления; К₁, К₂, К₃, К₄, К₅, К₆, К₇– коэффициенты пропускной способности сужающих устройств.

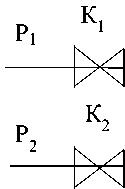
Р

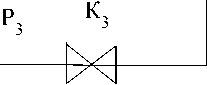
Рисунок 2 – Схема гидравлической системы

Исходные данные:

К1 = 0,7; К2 = 0,4; К3 = 0,8; К4 = 1,5; К5 = 2;К6 = 1; К6 = 1;К7 = 2,1. Р1 = 3; Р2 = 2,5; Р3 =2; Р4 = 1; Р5 = 0,5; Р6 = 0,9.

Далее была построена математическая модель.

Расход через сужающее устройство определяется уравнением:

и = Kjp - P ,                   (1)

где P 1 - давление до сужающего устройства; P 2 - давление после сужающего устройства; K - коэффициент пропускной способности сужающего устройства.

Определим уравнения расходов через сужающие устройства гидравлической системы, а также давления в точках разветвления системы:

41 = МР1 - Ри,   U2 = Кг^Рг - Р11,  U3 = К3^Р3 - P1V

4 = МРг1 - Р12,  4 = К5^Р12 - Р4,  4 = К6^Р12 - Р5,

47 = МР12 - Р6.

Необходимо добавить 2 уравнения, чтобы система уравнений имела решение (9 переменных - 9 уравнений).

и1 + и2 + и3-и4 = 0, U4-U5-U6-U7 = 0.

Для выбора алгоритма математической декомпозиции необходимо построить и проанализировать информационную матрицу системы уравнений математического описания, которая представляет собой квадратную матрицу, строки которой соответствуют номерам уравнений, а столбцы - обозначению определяемых переменных. Информационная матрица представлена в таблице 1.

Каждая строка матрицы соответствует определённому уравнению. Каждой неизвестной переменной соответствует определённый столбец. Наличие переменной в том или ином уравнении обозначается символом на пересечении соответствующей строки с соответствующим столбцом.

Данные символы обозначают следующее:

[+] - начальное приближение;

<+> - в данном уравнении переменная определяется при известных значениях остальных переменных;

(+) - переменная косвенно определена другим уравнением.

Таблица 1 - Информационная матрица системы уравнений, описывающей стационарный режим гидравлической системы

Номер уравнения	U	U2	U3	U 4	U 5	U s	U 7	Р11	Р12	Порядок решения
1	<+>							[+]		1
2		<+>						(+)		2
3			<+>					(+)		3
4				(+)				(+)	<+>	5
5					<+>				(+)	6
6						<+>			(+)	7
7							<+>		(+)	8
8	(+)	(+)	(+)	<+>						4
9				(+)	<+>	(+)	(+)			9

Если получаемое [ U3 (в решении 4) - U3 (в решении 3)] > £ , то необходимо методом половинного деления (или каким-либо другим числовым методом) выбрать новое начальное приближение (для данного примера р). Если U3 (4) = U3 (3) или U3 (8) - U3 (3) < £ , то модель определена.

На рисунке 2 представлена блок-схемы алгоритма вычислительных процессов.

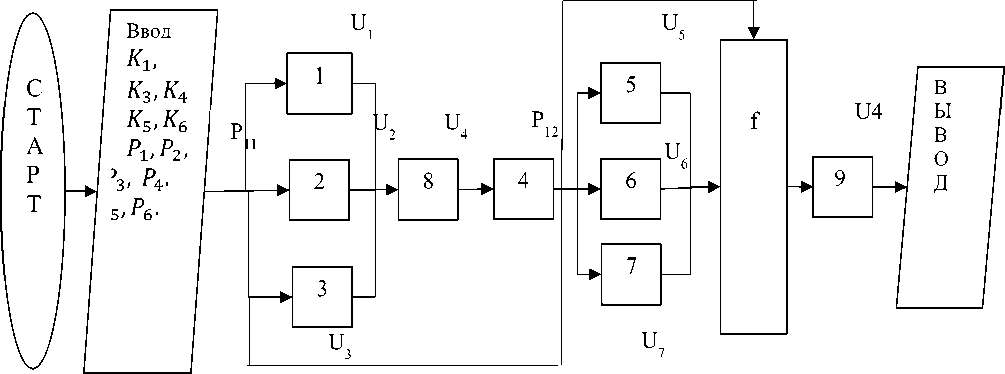
Рисунок 2 - Блок-схема алгоритма расчета гидравлической системы

Матрица уравнений была решена в математическом пакете Matlab. В результате были получены следующие параметры при заданном Р11=1.85.

U1 = 0.7507; U2 = 0.3225; U3 = 0.3098; U4 = 0.3098;

U5 = 0.0177; U6 = 0.7071; U7 = 0.6638; P12 = 0.9999.

Как видно из информационной матрицы системы уравнений, параметр U 5 можно найти двумя способами. Результат, полученный по порядку решения 4 –U₅=0.0177; результат, полученный по порядку решения 8 – U 5 =0.0177. Так как полученные результаты равны, можно сделать вывод о том, что модель определена.

Построим график (рисунок 3), иллюстрирующий зависимости значений полученных расходов через сужающие устройства от заданных P 11 . В первом случае P 11 =1.85, во втором случае P 12 =2.

В таблице 2 представлены Значения расходов U при заданных Р 11 . Таблица 2 – Значения расходов U при заданных Р 11

P 11	P 12	U 1	U 2	U 3	U 4	U 5	U 6	U 7
1.85	0.9999	0.7507	0.3225	0.3098	1.3830	0.0177	0.7071	0.6638
2	C	0.7	0.2828	0	0.9828	1.5109	1.0347	1.7198

На рисунках 3 и 4 представлены графики зависимостей полученных расходов через сужающие устройства от заданного Р 11 =1,85 и Р 11 =2 соответственно.

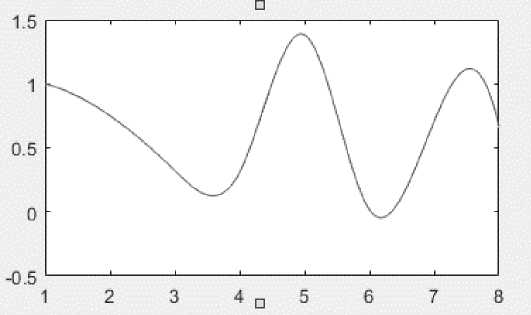
Рисунок 3 – Зависимость значения полученных расходов от Р11=1,85

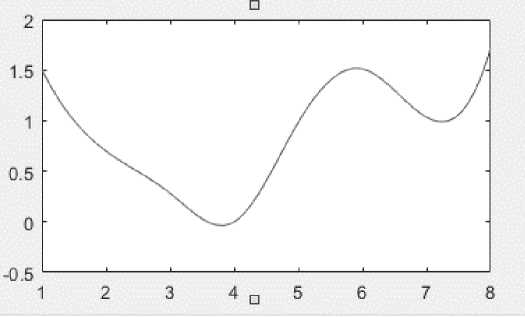
Рисунок 4 – Зависимость значения полученных расходов от Р 11 =2

В таблице 3 представлены рассчитанные U1 и U4 и при заданном Р11.

Таблица 3 - Значения расходов U1 и U4 и при заданном Р11

P 11	U 1	U 4
0	1.2124	2.9763
1.5	0.8573	1.8230
3	0	1.0828
4.5	0.8573	2.68
6	1.2124	3.560
7.5	2.6879	4.2555
9	1.7146	4.8510

На рисунках 5 и 6 изображены соответственно графики Зависимости расходов U1 и U4 при заданном Р11.

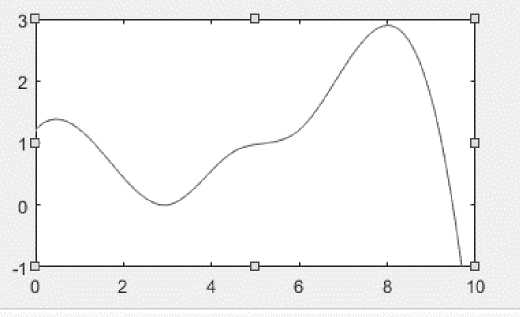
Рисунок 5 – Зависимости расходов U1 при заданном Р11

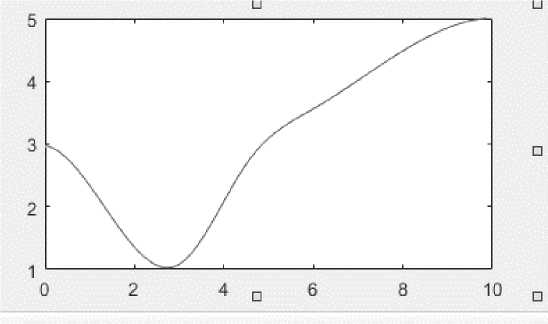
Рисунок 6 - Зависимости расходов U 4 при заданном Р 11

Таким образом, получено, что значение расходов через сужающие устройства от заданных Р11=1,85 и Р11=2 имеет неравномерный, скачкообразный колебательный характер, а к U₄ приближается к 0.