Математическое моделирование прыжка кошки

Кошка самое грациозное создание в мире. Её тело состоит из 244 костей и около 500 мышц. При помощи математического моделирования можно представить сложные системы в виде простых объектов, умеет описывать их математическими и физическими формулами. Что же касается биомеханики, то она пользуется спросом: исследования в данной области применяются при создании протезов.

В данной работе рассматривается сам механизм прыжка: как изменяются углы при сгибании и разгибании конечностей в полете; насколько кошка может прыгнуть в длину и как это осуществляется. Так же будет рассмотрена двухзвеньевая модель кошачьего тела. С помощью данной модели можно получить допустимые нагрузки на суставы при приземлении.

При создании математической модели «нормы» были приняты следующие допущения:

• -    Ограничения на гибкость суставов отсутствуют. Суставы не деформированы и с медицинской точки зрения не имеют иных патологий;

• -    Кости голени и бедра, запястья и заплюсны представлены абсолютно твёрдыми стержнями;

• -    Суставы представлены шарнирами, трение в которых минимально или отсутствует;

• -    Кости заплюсны/запястья, плюсны/пясти, пальцы представлены в виде материальной точки, т.к. имеют ограниченное движение;

• -    Кости таза и тазобедренный сустав рассматриваются как материальная точка, в которой сосредоточена масса оставшейся части тела кошки [1-3].

В модели рассматриваются:

• -    Бедренная кость/Плечевая кость

• -    Большеберцовая кость (Голень) /Лучевая кость (Предплечье). Рисунок 1.

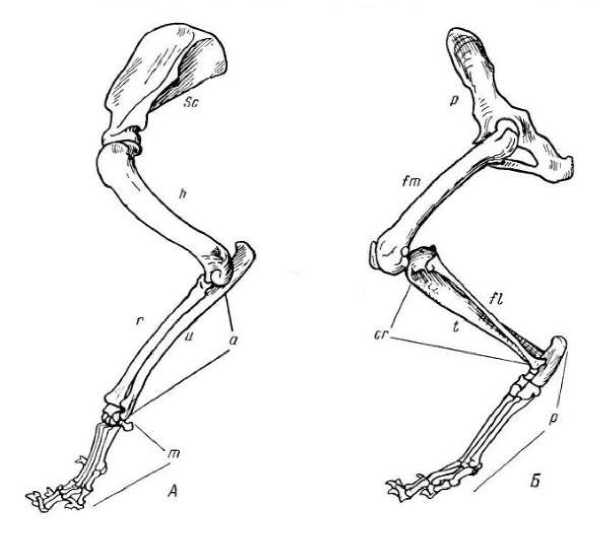
Рис. 1 Передняя и задняя конечность кошки sс — лопатка (scapula); h — плечевая кость (humerus); а — предплечье (antebrachium); u — локтевая кость (ulna); r — лучевая кость (radius); m — кисть (manus); р — таз (pelvis); fm — бедренная кость (femur); cr — голень (crus); t — большая берцовая кость (tibia); fi — малая берцовая кость (fibula); р — стопа (pes).

Двухзвеньевая модель задней конечности кошки (рисунок 2) При описании движения модели использовались обобщённые координаты: q 1 , q 2 , которые представляют собой углы между звеньями задней конечностью и вертикалью. Кроме того на рис. 2 обозначается длина бедра l 1 , длина голени l 2 ; расстояние r 1 от тазобедренного сустава до точки S 1 , в которой сосредоточена масса бедра (центр массы бедра), расстояние r 2 от коленного сустава до точки S 2 , в которой сосредоточена масса голени (центр масс голени); N_x и N_y - компоненты реакции опоры [11].

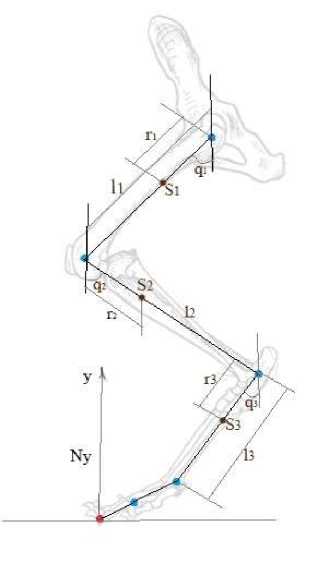
Рис. 2

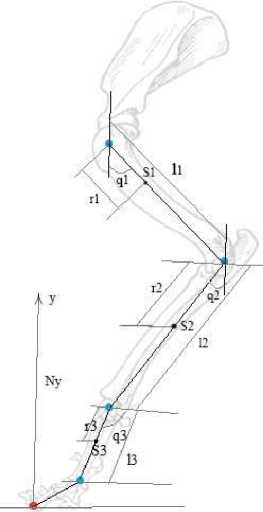
Рис. 3

Модель задней конечности кошки Модель передней конечности кошки

Двухзвеньевая модель передней конечности кошки (рисунок 3) Для описания движения модели используются обобщённые координаты: q ₁ , q ₂ , которые представляют собой углы между звеньями передней конечности и вертикалью. Длина плечевой кости l ₁ , длина лучевой кости l ₂ ; расстояние r ₁ от плечевого сустава до точки S 1 , в которой сосредоточена масса плеча, расстояние r 2 от локтевого сустава до точки S 2 , в которой сосредоточена масса лучевой кости; N _x и N _y - компоненты реакции опоры [10].

На рисунках 4-7 обозначены R x и R y - вертикальная и горизонтальная составляющие силы реакции в коленном/локтевом суставе, F x и F y -вертикальная и горизонтальная составляющие силы реакции в тазобедренном/плечевом суставе, N x и N y - вертикальная и горизонтальная составляющие реакции опоры.

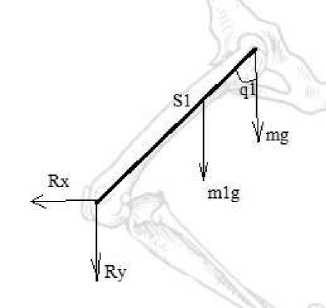
Рис.4

Силы, действующие на бедро

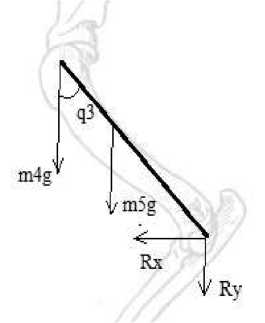
Рис.6

Силы, действующие на плечо

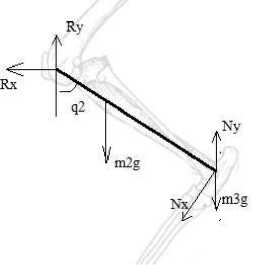
Рис.5

Силы, действующие на большеберцовую кость

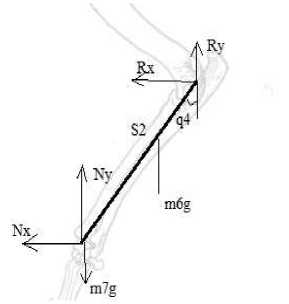
Рис.7

Силы, действующие на предплечье

Что касается костей плюсны/пясти, пальцев, то они были представлены в виде материальной точки, т.к. имеют ограниченное движение.

Так подушечки лап у домашней кошки построены из плотных мякишей (pulvini) — производных кожи. Это упругие утолщения кожного покрова на пальмарной (плантарной) стороне лапы. Они гораздо тверже, чем обычная кожа, связывают воедино кости «стопы», а также помогают при торможении. Упругость связана с подкожным слоем, т.к. он сильно развит и несколько своеобразен: между грубыми пучками коллагеновых и эластических волокон заложены прокладки жировой ткани. В результате получается упругая и удобная для опоры подушка, которая служит основной частью мя- киша.

Рассмотрим работу ног кошки в теории при прыжке. Кошка приседает и начинает резко вставать. Обозначим силу ее лап за F . Эта сила подымает её вверх. Ей противодействует сила тяжести P . Она равна весу кошки:

P = mg                             (1)

Где m – масса кошки, g – ускорение свободного падения.

Вспоминаем Второй закон Ньютона. Равнодействующая сил, действующих на тело, равна массе тела m , умноженной на его ускорение a :

F – P = ma                         (2)

Кошка, быстро вставая, с одной стороны, совершает работу против силы тяжести P = mg , поднимая своё тело вверх. С другой стороны, она разгоняет своё тело с ускорением a до некоторой скорости V . В результате центр тяжести тела, получив скорость V , подлетает до высоты h :

V2

² g

Во время подъёма вверх, кошка движется с ускорением а (уравнение 2). Это ускорение может значительно изменяться, потому что сила лап зависит от величины сгиба в суставах. Если мы возьмём среднее ускорение, то для него будет применимо уравнение (3):

V^г z = —

2 a

Чтобы решить задачу, надо знать, как сила лап зависит от глубины приседа, а затем взять интеграл? Да.

Элементарная работа dA равна силе F , умноженной на бесконечно малое перемещение dx :

dA = F dx                              (6)

Возьмём интеграл от этого выражения:

A = J F ( x ) dx                           (7)

- z

Пределы интегрирования нужно взять от максимальной глубины приседа (– z ), до исходного положения (0). Чем глубже кошка присядет, тем большую работу совершат её лапы. На что же тратится эта работа:

– На поднятие своего тела в поле тяжести;

– На разгон тела, в результате которого тело получает кинетическую энергию:

A = J F ( x ) dx

- z

mV² = mgz +——

Благодаря тому, что тело имеет кинетическую энергию, оно подлетает на высоту h. Поэтому:

mVг     ,

—-— = mgh

С учётом этого уравнения, изменяем уравнение (8) и получаем:

A = J F ( x ) dx = mgz + mgh = mg ( z + h ) - z

Итак, кошка приседает и прыгает вверх. Работа его ног определяется интегралом (7). С другой стороны эта работа равна (8). Благодаря данным уравнениям можно вычислить длину прыжка кошки, работу (нагрузки) ее конечностей [5-7].

Вернемся к конструкциям. Для каждой части конструкции можно записать второй закон Ньютона и уравнение вращательного движения.

Для бедра и плеча уравнения имеют вид:

m1(5)a1(5) + ma = m1(5)g + Rx + Ry + m(4)g(11)

m1(5)xn + mx(4) = – Rx(12)

m1(5)yn + m(4)y = ry – g(m1(5) + m)(13)

I1(5)q1(5) + mr21(5) q1(5) + r (Fsin q – Fcosq1(5)) + (l – r1(5))(Rx – Rysinq1(5))(14)

Где координаты центра масс определяются формулами:

xn = l2 sin q2(4) – (l1 – r1 )sin q1(3)

yn = l2 cos q2(4) + (l1 – r1 )cos q1(3)

y = l2 cos q2(4) + l1 cos q1(3)

x = l2 sin q2(4) – l1 sin q1(3)

Для голени и предплечья уравнения имеют вид:

(m2(6) + m3(7) )a2 = Nx+ Ny+ Rx+ Ry+ (m2(6) + m3(7))g ,(19)

(m2(6) + m3(7) )xp = Rx + Nx ,(20)

(m2(6) + m3(7))yp = Ny – Ry – (m2(6) + m3(7))g ,(21)

q 2 ( I 2 + m 3 (7) ( l 2 – r 2 ) ²)=( l 2 – r 2 )(( N y – m 3(7) g ) sinq 3 – N x cosq 4 )+ r 2 ( R x cosq 2 + R y sinq 2 )

Где координаты центра масс голени и предплечья определяются фор- мулами:

x p = (l 2 – r 2 )sin q 2(4)

y p = (l 2 – r 2 )cos q 2(4)

Из уравнений (12), (18), (24) и (13), (19), после преобразований получается:

N x = (m 2(6) + m 3(7) )x p + ma x + m 1(5) x n ,                                      (25)

N y = (m 2(6) + m 3(7) )y p + ( m 2(6) + m 3(7) )g + m 1(5) y p + m 1(5) g + mg.           (26)

Данные реакции подставляются в уравнения (14) и (20).

С помощью представленной выше теоретической модели задней и передней конечности можно решать несколько типов задач, например задачи о прыжках. Целью данной работы является исследование приземления. При этом по известным зависимостям углов q 1(3) ( t ) и q 2(4) ( t ) находятся сила реакции опоры и нагрузки на суставы [4].

Так же при полете кошка, будто плавно плывёт по воздуху. Это можно описать зависимостью изменения углов в суставах от времени:

q(t) = a + be-ct , где коэффициенты a, b, c определяются следующим обра- зом: a = q™, b = q ~ q max, с = — — ln tn

q n

—

q max

V q 0 q max J

где q – известное значение угла в момент времени t, а q0 и qmax начальные и конечные значения углов.

Для нахождения значения углов нам понадобились экспериментальные данные. Также были взятые в «норме» среднестатистические параметры домашней кошки из учебников по ветеринарии.

Моменты инерции конечностей можно вычислить по формуле момен- та инерции стержня: I =

ml ²

. 12

Стоит отметить, чем больше момент инерции конечности, тем больше энергии ей требуется сообщить. Поэтому для уменьшения необходимой для движения кинетической энергии, выгоднее, чтобы обладающая значительной массой мускулатура была расположена не по всей длине конечности, а ближе к бедру или плечу. У млекопитающих, способных к быстрому бегу, много мышечной ткани находится в проксимальных (ближних) частях конечностей и мало – в дистальных (дальних) частях [8].

Таблица –1. Характеристики частей тела кошки

Величина	Значение	Единица измерения
Рост (с хвостом)	80	м
Масса тела	4	кг
Масса бедра	0,12	кг
Масса голени	0,1	кг
Масса задней лапы	0,06	кг
Длина бедра	0,105	м
Длина голени	0,095	м
Положение центра масс Бедра/плеча (величина r 1)	33/30	% от длины сегмента тела
Положение центра масс Голени/предплечья (величина r 2 )	32/31	% от длины сегмента тела
Момент инерции бедра/плеча	0,0001102/0,000083	кг·м2
Момент инерции голени/предплечья	0,000075/0,000055	кг·м2
Масса плеча	0,1	кг
Масса предплечья	0,06	кг
Масса передней лапы	0,04	кг
Длина плеча	0,1	м
Длина предплечья	0,105	м

Данные среднестатистические параметры кошки можно применять и вставлять в полученные математические формулы.

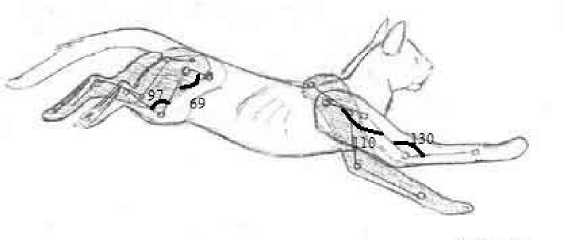
Схема 1. «Полет» кошки

У кошки плечевой и тазобедренный суставы шаровидные, многоосные, в то время как у лошади эти суставы имеют только пару осей движения [9].

Поэтому кошка имеет грацию при прыжке. В схеме 1 представлены приблизительные параметры углов в суставах. Данную схему также можно представить в виде таблицы:

Таблица – 2. Значение углов при статике q ₀ и максимальное значение при прыжке q _max

	q 0	q max
Для тазобедренного сустава	84о	69о
Для коленного сустава	63о	97о
Для плечевого сустава	88о	110о
Для локтевого сустава	71о	130о

Время прыжка в среднем 3 сек. На рисунке 8 показана зависимость углов от времени для прыжка:

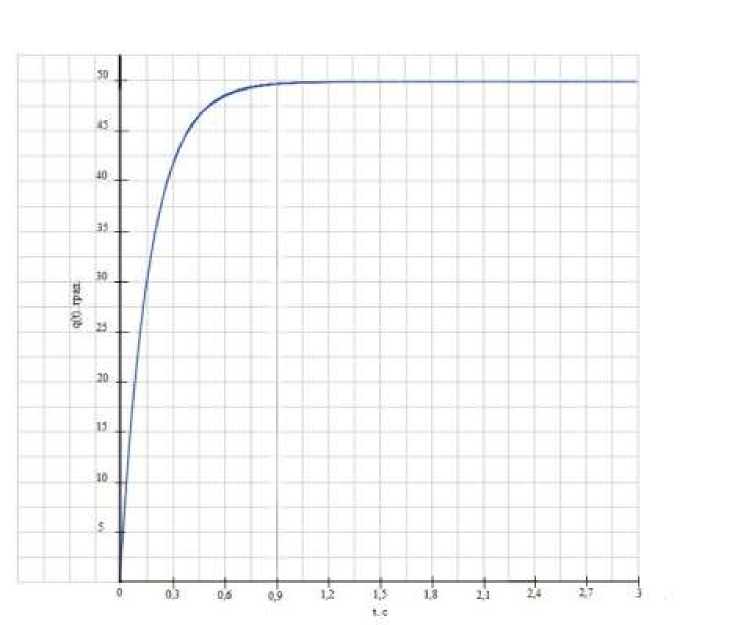
Рис. 8 Зависимости углов наклона бедра от времени для типичного прыжка

Аналогично можно вычислить углы наклона голени, плеча и предплечья. В результате стало известно, что чем больше угол сегмента относительно вертикали при приземлении, тем «мягче» будет само приземление. Говоря о прыжках, стоит упомянуть и падение кошек. В 1894 году впервые физиолог Марей представил снимки кошек в различных фазах падения. Оказалось, что кошка без хвоста падает так же, как и полноценная здоровая кошка. Тогда была выдвинута гипотеза о том, что животное получает импульс в момент отделения от рук экспериментатора, так, как это происходит у прыгунов в воду с вышки. На фотоснимках Марея видно, что кошки управляли своим телом и когда их бросали без импульса. В начале 20 века феномен был разрешен и вошел во все учебники физики. В падении кошка изменяет положение тела за счет энергичных действий туловища и конечностей. Однако кошка, брошенная "солдатиком", все же может упасть. В 1960 году американец Макдональд объяснил, почему кошки, падая с любой высоты, всегда приземляются на четыре лапы, применяя скоростную съемку для выяснения падения кошки. Выяснилось, что при движении вверх, она летела вверх лапами до высшей точки полета, а далее переворачивалась.

Вторым вопросом «кошачьего парадокса» является то, что животное не разбивается, упав с высоты, относительно смертельной для человека. Кроме того, кошка имеет более сильные по отношению к собственному весу мышцы, чем у человека, которые представляют собой отличный амортизатор. Однако еще не доказан момент сохранения импульса для падения и прыжка кошки, а наука «пазематология» остается всего лишь красивой «теорией», не имеющей авторитетности. Можно лишь представлять математические модели, которые помогут в изучении движения и построения протезов для данного вида.