Математическое моделирование пульсовых волн на основе теории солитонов и уравнения Кортевега де Фриза

Введение. С точки зрения восточной медицины пульс – источник, в котором закодирована информация о состоянии всего организма в целом. Используя методы восточной медицины, можно быстро, но при этом довольно качественно провести исследование пациента. В упрощенном варианте данный процесс можно представить так [2]:

• 1)    варьируя силу нажатия и участок соприкосновения попеременно на левой, правой и обеих руках, пульсодиагност поочерёдно опрашивает 12 внутренних органов (сердце, тонкая кишка, лёгкие, толстая кишка, селезёнка, желудок, левая почка, половые органы, печень, желчный пузырь, правая почка, мочевой пузырь);

• 2)    результаты опроса соотносятся с "врождённым пульсом" пациента, сезонными, суточными особенностями пульса и его психофизиологическим типом по восточной системе;

• 3)    выносится диагноз.

Учитывая тенденции развития медицины превентивного действия, данный подход вызывает большой практический интерес.

С точки зрения физики течение крови – довольно сложный процесс, многие исследователи даже называют его третьим режимом течения. Сложности при моделировании данного процесса обусловливаются множеством факторов: как «чисто физическими» (например тем, что кровь сама по себе является неньютоновской жидкостью, течение крови происходит по сосудам и венам), так и тем, что приходится учитывать различные регуляционные функции организма. По этой причине большинство моделей, основанных на теории математической гемодинамики, довольно сложны и трудно применимы.

В настоящее время известны попытки математического моделирования пульсовой волны, например модель Волобуева на основе нелинейного уравнения Шредингера (Волобуев А.Н., 1995, 3), модель Акулова, представляющая собой произведение экспоненциальной и тригонометрической функции с тремя параметрами (Акулов В.А., 2006), модель Самарского, основанного на законе сохранения энергии и импульса (Самарский А.А. с соавт., 1996), модели на основе численных методов (Бороноев В.В., 1999) и др. (Астраханцева Е.В., Гидаспов В.Ю, Ревизников Д.Л., 2005). Каждая из этих моделей и подходов имеет свои достоинства и недостатки, и все же они остаются далеко несовершенными по сравнению со сложностью данного биофизического явления в организме человека, которая, возможно, и оправдывает его информативность.

В данной работе рассматривается возможность моделирования пульсовой волны при помощи теории солитонов, поскольку характер реальной пульсовой волны во многом схож со свойствами соли- тонов. Напомним, что солитонами называются любые локализованные нелинейные волны, которые взаимодействуют с произвольными локальными возмущениями и всегда восстанавливают асимптотически свою точную первоначальную форму с некоторым сдвигом фазы [4]. Другими словами, основное предположение заключается в том, что по природе пульсовая волна состоит из комбинации определенного количества импульсов (единичных волн), исходящих из различных органов и систем организма и являющихся взаимодействующими компонентами пульсовой волны. Таким образом, математическое представление одного импульса – это один солитон. Следовательно, математическая модель пульсовой волны – это система из определенного количества солитонов, взаимодействующих между собой и имеющих набор параметров, определяющих все возможные его состояния. И центральную роль в предлагаемой модели играют свойства упругого взаимодействия между солитонами и солитонов с локальными возмущениями. Мы рассматриваем пульсовую волну, не принимая во внимание процессы регуляции кровотока, как распространение уединённых волн (пульсовой) в эластичной тонкостенной трубке. В результате анализа научной литературы по теории солитонов наиболее подходящим по классу моделируемых систем выбрано уравнение Кортевега де Фриза, имеющее солитонные решения, состоящие из солитонной и несолитонной части [1,4,5,6,7].

Солитонное решение уравнения Кортевега де Фриза (далее КдФ). Итак, рассматривается уравнение КдФ следующего вида:

K (u) = ut + 6uux + uxxx = 0 ,                                                               (1)

где u(x, t) – потенциал пульса; t – глобальное время одной моделируемой волны; x– локальное вре- мя одного моделируемого сердечного цикла.

В работе [1] представлен способ формирования N-солитонного решения данного уравнения методом Хироты. Общее решение уравнения КдФ состоит из солитонной и несолитонной части. В нашем случае рассматривается решение, в котором локальные возмущения (несолитонная часть) пренебрежимо малы. То есть мы строим в некоторой степени идеализированную модель, в которой не учитываются малые локальные возмущения [7,5]. Хирота показал, что в общем виде N-солитонное решение уравнения (1) имеет вид:

u ( x , t ) = 2 d-^ In F , dx ²

где F – определитель некоторой матрицы.

Получение 5-солитонного решения уравнения КдФ. Опуская промежуточные выкладки процесса получения N -солитонного решения, представим результат получения функции F в общем виде [1]:

FN = Z exP

M = 0,1       ^ i = 1

^Л N        N

У мп, + Z Mj

1 < i <  j

\

где M i = 0 или 1; e A

ki - kj) к ki + kj j

n i = k i x + ^ - h i ; k i , ^ i , n ° , i = i, N

– параметры системы.

В результате подстановки (3) в (2) и определенных упрощений получаем следующий вид потенциала u(x,t) :

N u (x, t) = Z ui( x, t) + a( x, t),                                                                                      (4)

l = 1

z       1,2...1.2 ( kx-Wit+h ]

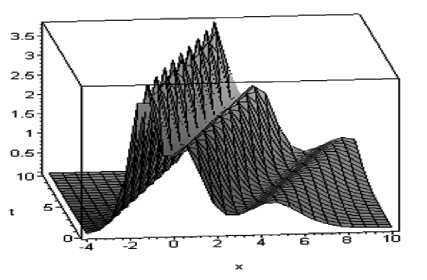
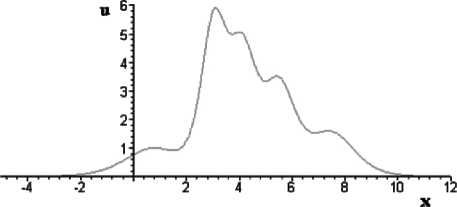
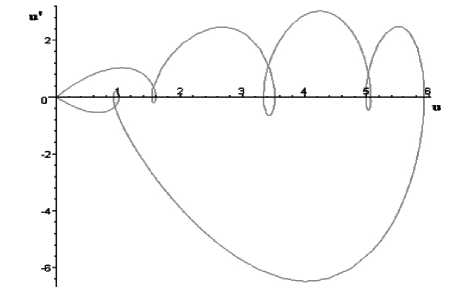
где ui(x,t) = —ki sech I ——L I,

N

|^(x, t)| ^ У u, (x, t) .

i =1

При этом локальные возмущения достаточно сильно усложняют систему, получается довольно громоздкое решение. Поэтому предлагается рассмотреть потенциал (4) в следующем виде:

N и (x, t) ~^ и, (x, t)

i=1

.

Соответственно система (3) принимает вид при t=0:

N+ и (x) = 2L k^,2sech2 i----L и 2 i V 2   )

.

В результате расчетов при N=5 получено 5-солитонное решение:

и (x, t) = 2-^—ln F,

^,        dx^{2     5}

где F₅получаем из формулы (2), при N=5. Потенциал u (напряжение пульсовой волны) представляет собой сложную функцию из комбинаций показательных функций с основанием exp (e).

Идентификация параметров, входящих в решение. В полученное решение (5) входит ровно 3 х N параметров, т.е. при N=5 ровно 15 параметров, через которые определяются переменные ni = kix + го it - hi⁰, где ki, to,, n,, i = 1..5 - параметры данной системы. В результате различных расчетов были получены следующие соотношения:

• 1.    Амплитуда i-го солитона, плотно не взаимодействующего с другими солитонами, прямо про-

• порционально зависит от соответствующего параметра ki, а именно umaxi = 2 ki . При плотном взаимодействии i-го, допустим, с i+1 солитоном амплитуды i и i+1 солитонов возрастают на величину ri = g (ki, ki+1) и ri+i = g (ki+i, ki) , где g - неизвестная функция;

• 2.    Аргумент точки максимума i-го солитона определяется следующим выражением:

  x maxi

  
  

  -tot + A<⁰⁾ —

• 3.    Скорость по фазе (с) определяется как отношение коэффициентов при x и t . Для i-го солитона она равна ci = ^юу, . В данном случае целесообразно брать все фазовые скорости одинаковыми, так k_i

k

как реальную пульсовую волну предполагаем не меняющейся во времени или хотя бы на некотором промежутке времени. То есть рассматривается частный случай: c1 = c2 = c3 = c4 = c5. Отсюда получаем, что график модели пульсовой волны не меняется со временем, а просто осуществляется перенос графика на величину cКt. Например, 3-солитонное решение, где фазовые скорости солитонов равны, наглядно представлено на рисунке 1.

Рис. 1. Реализация 3-солитонного решения по времени с равными скоростями

Построение солитонного решения с параметрами реальной пульсовой волны

Если известны численные значения локальных максимумов, т. е. значение координат вершин каждого «горба» реальной пульсовой волны, то можно построить модель, соответствующую данной пульсовой волне. Для этого значения всех пяти вершин заносятся в приведенную ниже таблицу исходных данных.

Потенциал (u)	u1	u2	u3	u4	u5
Фазовая координата пиков (x)	x1	x2	x3	x4	x5

Далее, используя соотношения, полученные при идентификации параметров, построена система уравнений следующего вида:

• 1    ,—

• - k2 = u,,  i = 1,5;

• 2    i i

• -9 + h⁽⁰⁾

  --i-----i— = x,, i ki‘

• ⁹ = ^i+L,  i = 1,4;

I ki

Данная система состоит из 14-ти уравнений и имеет 15 неизвестных. Для получения единственного решения предлагается задать произвольное значение одного из неизвестных параметров. Например, <91 = 1, тогда данная система должна иметь единственное решение в виде числовых значений всех параметров модели. Подставив параметры в решение, мы получаем функцию u=u(x) (из-за довольно громоздкого аналитического вида функции здесь она не приводится). Ниже представлены график этой функции с параметрами реальной пульсовой волны здорового человека и его фазовый портрет (рис. 2 и 3).

Рис. 2. Потенциал с параметрами реальной пульсовой волны здорового человека

Построенный график на рисунке 2 в достаточной степени точности повторяет контур реальной пульсовой волны. Из ранее проведенных исследований в данной области [2] известно, что фазовый портрет пульсовой волны здорового человека должен иметь вид, напоминающий форму сердца, что соответствует полученному графику на рисунке 3.

Рис. 3. Фазовый портрет функции u=u(x)

Заключение. В работе рассмотрен один из возможных подходов моделирования пульсовых волн человека на основе солитонного решения уравнения Кортевега де Фриза. С помощью метода Хироты получено 5-солитонное решение. Проведены расчёты в среде Maple 8, построены график и фазовый портрет по параметрам реальной пульсовой волны.

Е.В. Дрыганова. Магистральное решение в дискретной модели регионального развития

Таким образом, данный подход заслуживает более глубокого исследования. Детального изучения требуют параметры и характеристики данной системы, а также их связь с физиологическими процессами. В перспективе возможно введение в модель локальных возмущений для моделирования высокочастотных составляющих пульсовой волны.