Математическое моделирование работы 3D-сканера при контроле зеркальной системы обсерватории "Миллиметрон"

Одним из основных направлений развития бортовых космических технологий является создание многозональных высокоапертурных зеркальных телескопов, обеспечивающих сбор и обработку информации в диапазонах спектра излучения от рентгеновского до миллиметрового. Примером этого служит проект космической обсерватории «Миллимет-рон» (Спектр-М), рассчитанный для работы в миллиметровом и дальнем ИК-диапазонах (70 мкм – 10 мм) с 10-метровым охлаждаемым (~4,5 K) криогенным телескопом [1 –3]. Главной проблемой создания крупных телескопов является обеспечение качества изображения, что, в свою очередь, требует раз- работки высококачественных и высокоточных методов контроля формы составных элементов их зеркальной системы [4–7]. Например, в [7] дан прекрасный обзор состояния и тенденций развития космического телескопостроения за рубежом. Изложены результаты проводимых в ряде ведущих стран работ по проектированию и строительству (с акцентом на новые материалы для зеркал) совершенных оптических систем наблюдения за космосом. Основное направление – создание больших оптических телескопов. Рассмотрены находящиеся на орбите и строящиеся большие оптические телескопы с составными и гибкими зеркалами, управляемыми активными системами с целью устранения деформаций на всех этапах изготовления и эксплуатации.

Создание различных систем контроля формы составных элементов таких телескопов требует разработки математических моделей и алгоритмов работы данных контрольных систем [8– 16]. В частности, в [8] изложена модель процесса юстировки составных зеркал высокоапертурных телескопов. На основе введенного понятия разностной поверхности с использованием разработанных алгоритмов геометрического и оптотехнического позиционирования зеркальных сегментов получены соотношения для оценки точности юстировки составных зеркал. В [16] кратко представлены методы юстировки и калибровки информационно-измерительных систем на борту космических аппаратов оптико-электронного и радиоэлектронного наблюдения. Эти методы основаны на известных приемах сглаживания – аппроксимации, фильтрации векторных измерений и интерполяции результатов фильтрации векторными сплайнами.

По результатам предварительного анализа бесконтактных систем контроля геометрических параметров, входящих в состав КА (и геометрических, и интерферометрических), наибольший интерес представляют приборы, созданные по принципу 3D-сканера, как наиболее оптимальные для решения отраженных в настоящем сообщении задач. Например, компания Jena-Optronik Gmbh успешно разработала и применила на практике 3D-лидар / сканер RVS-3000-3D для космических применений 181/contributions/1454/attachments/1361/1586/2017_CS . 3D-сканер был успешно протестирован в нескольких космических программах Европейского и Японского космических агентств в основном в операциях по стыковке космических аппаратов. К настоящему времени отечественные 3D-сканирующие системы космического применения в открытой печати нами не зафиксированы.

Описываемая в настоящем сообщении оригинальная система контроля зеркальной системы обсерватории «Миллиметрон» (СК ЗС) и не имеющие аналогов математическая модель и алгоритмы ее работы создаются для штатного функционирования в составе бортового комплекса научной аппаратуры обсерватории «Миллиметрон» и рассчитываются на работу в условиях космического пространства. СК ЗС в силу огромного динамического диапазона контроля (≥ 10 ⁶ ) состоит из двух самостоятельных ступеней – предварительной (3D-сканер) и окончательной (Анализатор). В настоящем сообщении описывается моделирование работы только предварительной ступени. Она предназначена для контроля качества зеркальной системы (ЗС) космического телескопа и использования данных, получаемых СК ЗС в качестве сигналов «обратной связи» для предварительной настройки и юстировки оптической системы телескопа в космическом пространстве с формированием в фокальной плоскости телескопа пятна диаметром не более 50 мм.

1.    Телескоп «Миллиметрон» и основные задачи бортовой системы контроля

Антенна телескопа представляет собой 2-зеркальную оптическую систему, построенную по схеме Кассегрена. Она состоит из главного параболического и вторичного гиперболического зеркал. Диаметр главного зеркала составляет 10 метров, что слишком велико для существующих обтекателей ракет-носителей, поэтому конструкция зеркала будет раскладывающейся. Оно состоит из нераскладывае-мой центральной части, диаметром 3 метра, и раскрываемой части, состоящей из 24 лепестков.

Ключевые параметры антенны «Миллиметрона» достигаются за счет нескольких оригинальных конструктивных решений:

• •    Материал для отражающей поверхности панелей и основной конструкции лепестков – углеродное волокно, армированное пластиком (CFRP). Данный материал обеспечивает высокий удельный модуль и низкий коэффициент теплового расширения.

• •    Каждый лепесток главного зеркала состоит из каркаса и трех независимых отражающих панелей.

• •    Каждая панель устанавливается на каркас лепестка с помощью трех линейных актюаторов.

• •    Регулировка панелей будет осуществляться бортовой активной системой контроля поверхности.

Данные решения позволят корректировать отклонения положения панелей, связанные с процессом раскрытия, а также искажения поверхности, связанные с температурными эффектами [3].

Оптическая схема зеркальной системы обсерватории (телескопа) «Миллиметрон» приведена на рис. 1.

Телескоп может быть представлен в виде физической модели, состоящей из множества оптических отражающих поверхностей (ОП) со стабильной формой. Совокупность всех ОП телескопа назовем зеркальной системой телескопа. Примерами таких ОП являются (см. рис. 1): вторичное зеркало (ВЗ); переключающее зеркало (ПЗ); любая из панелей (фрагментов) многоэлементного параболоида главного зеркала (ГЗ).

Глобальная система координат (ГСК) телескопа определяется положением начала координат и координатными осями. Вершина параболоида ГЗ принимается за начало ГСК, в предположении идеальной формы параболоида ГЗ. Вектор оси X ГСК направлен вдоль оси параболоида ГЗ от его вершины в направлении ВЗ. Вектор оси Y от центра ПЗ в сторону фокуса приемника, обозначенного как F 2 на рис. 1. Ось Z однозначным образом дополняет оси X, Y, образуя полный ортогональный базис из векторов X, Y, Z ГСК, при котором ГСК является правой системой координат.

Однозначное положение каждой ОП как поверхности твердого объекта в пространстве определяется:

• -    выбранной базовой точкой на твердом объекте, содержащем ОП . Положение этой базовой точки объекта определено ее координатами в ГСК;

  – тремя углами поворота объекта с ОП относительно его базовых осей в ГСК (углы Эйлера).

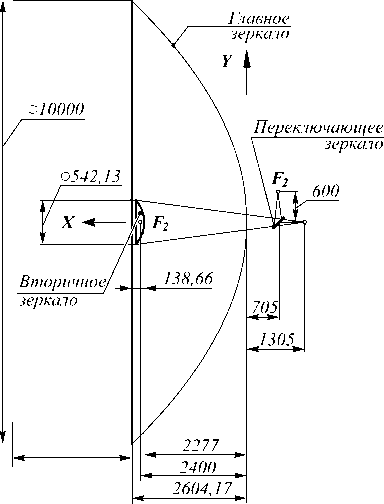
Рис. 1. Оптическая схема зеркальной системы обсерватории «Миллиметрон». Расчетные характеристики: главное зеркало – параболическое: радиус кривизны при вершине R ГЗ = 4800 мм; диаметр главного зеркала D ГЗ = 10000 мм. Вторичное зеркало – гиперболическое: R ВЗ = – 254,7337 мм; D ВЗ = 542,13 мм. Расстояние между ГЗ и ВЗ – 2277 мм. Эквивалентное фокусное расстояние – 70000 мм. Расстояние от ВЗ до фокальной плоскости – 3582 мм. Квадрат эксцентриситета ВЗ е² = 1,147452

В итоге, положение каждой ОП в модели телескопа задается 6 параметрами – тремя углами поворота объекта, а затем радиус-вектором смещения базовой точки объекта в ГСК.

Знание положения каждой ОП телескопа по ее (6 или иному достаточному количеству) собственным параметрам означает, что геометрия (или конфигурация) телескопа точно и однозначно определена в рамках данной модели. В таком случае возможна оценка оптического качества телескопа и его последующая настройка.

Обозначим полный набор параметров, описывающий положение всех ОП телескопа как вектор (набор) Х . Компоненты вектора содержат все параметры каждой ОП телескопа в его заданном состоянии.

Поэтому задачей СК ЗС является определение вектора неизвестных параметров Х по косвенным измерениям, получаемым в результате обмера телескопа 3D-сканером.

Для получения косвенной информации о геометрии телескопа в СК ЗС заложен 3D-сканер. 3D-сканер – это прибор, расположенный в «теплом отсеке» КА, который может запускать тонкий оптический луч в ЗС телескопа через временное оптическое окно между «теплым отсеком» и «холодной зоной» и «наблюдать» за всеми ОП из точки F 2 .

На поверхностях обмеряемых ОП расположены оптические контрольные метки (КМ), которые могут быть обмерены лучом 3D-сканера. КМ представляет собой металлический шарик (или сферическое зеркало с характерным диаметром не менее 10 мм)

3D-сканер состоит из 2 основных узлов. Первый узел представляет собой устройство, которое может излучать стабилизированное лазерное излучение под заданным углом, принимать рассеянное или отраженное излучение от предмета, который встретился на пути лазерного излучения, производить анализ пришедшего назад (принятого) излучения и по результатам анализа выдавать заключение о расстоянии между излучателем и предметом, который рассеял (отразил) излучение. Данное устройство будет в дальнейшем называться дальномерный канал.

Второй узел представляет собой устройство, обеспечивающее поворот направления излучения, направляемого к контролируемому объекту вокруг двух взаимно-перпендикулярных осей (угол места и азимутальный угол) практически на любой, наперед заданный угол, а также производить измерение данных углов с малой погрешностью. Данное устройство получило название углоизмерительный канал.

Работа предварительной ступени СК ЗС осуществляется следующим образом:

– выполняется обмер всех или подмножества КМ с использованием 3D-сканера. По каждой обмеренной КМ на выходе 3D-сканера формируются 3 канала измерения (с индексами m =0, 1, 2): m =0 – длина оптического пути ДК до КМ; m = 1,2 – два угла системы зеркал 3D-сканера (СЗ) при точном прицеливании на КМ,

• –    в результате обмера множества КМ получается набор измерений (по три измерения на каждую КМ), который обозначим как вектор Y;

  – известный (после обмера множества КМ) вектор Y будет использоваться для оценки и восстановления вектора неизвестных параметров телескопа X.

2.    Постановка задачи и практические выводы по итогам ее решения

Итак, имеем следующее:

• – положение телескопа однозначно определяется неизвестным вектором X ;

• – 3D-сканер СК ЗС может обмерять положения КМ (оптические контрольные метки), значения которых описываются функциями f m , k ( X );

  – функции f m , k ( ) известны (вычислением по чертежам КД) и предполагаются постоянными (независимыми от малого изменения аргумента X ).

На основе этих предположений решаем обратную задачу, то есть определим расстройку параметров ОП ( X ) от их исходного (идеального) положения по результатам обмера множества КМ ( Y ) 3D-сканером.

Пусть телескоп настроен, это соответствует настроенному положению всех его ОП, которые мы обозначим как вектор X = {xp }, состоящий из параметров xp . Сами параметры xp настроенного теле- скопа потенциально могут быть обмерены в заводских условиях, однако в этой информации нет необходимости, как это будет показано ниже.

При настроенном состоянии телескопа СК ЗС вы- полняет обмер всех ее КМ к = 0, .., K- 1 при помощи 3D-сканера по всем каналам измерения 3D-сканера m =0, 1, 2. Создается массив начальных измерений

f

Y { fmt , к }

(для настроенного телескопа на Земле), который соответствует настроенному вектору параметров X ЗС:

f m , k

= f m , к ( X ) = f _m , к ( X 0 , X 1 ,.

Y = { и ( X ) } .

. , ^X P - 1

Массив измерений настроенного телескопа Y запоминается. После вывода телескопа на орбиту и его раскрытия в рабочее положение ЗС телескопа расстроена, поэтому в новом положении телескопа на орбите его параметры ОП X = { x _p } случайно смещены по отношению к исходному (настроенному) состоянию.

Формулируем задачу следующим образом: определить изменения положения ОП от идеального настроенного x = { A x _p } = X - X по изменению положения КМ на орбите от их идеально настроенного У = { A f „ , к } = Y - Y .

При этом известна матричная зависимость (прямая задача) y = H × x , где H – вычисляемая по чертежам постоянная дизайн-матрица. То есть необходимо решить обратную задачу: x = x ( H , y ).

Было реализовано применение дифференциальных измерений КМ, т.е. попарная разница расстояний или углов каналов 3D-сканера до близко расположенных КМ существенно снизит систематическую ошибку измерения расстояний или углов 3D-сканера.

Чтобы формализовать такое преобразование общим способом (в виде линейной комбинации измерений), вводим матрицу преобразования первичных измерений D . Получаем новую замену переменных, m,n переводя первичные измерения y в дифференциаль-

D n,1

ные u , как u = D ■ у . D ’    D D D m ,1           m,1 m,n n ,1

Для решения задачи был вычислен матричный решатель (матрица) F такой, что оценка х неиз- p , m                                           p ,1

вестного вектора системных параметров х по диф- p ,1

ференциальным измерениям u есть m,1

X = F ■ u .                                            (3)

D D D                                           V 7

p ,1 p , m m ,1

При вычислении матрицы F необходимо было по- p,m добрать ее таким образом, чтобы отклонение

D = X - х истинного смещения х и его найденной p ,1 p ,1 p ,1                                                     p ,1

оценки х было минимально в статистическом смысле. p ,1

Подчеркнем, что Решатель – это вычисляемая оригинальная матрица, позволяющая оптимальным образом в линейном приближении найти все параметры х по измеренным значениям u . Даже p ,1                                                                    m ,1

краткий вывод формулы нашего оптимального Решателя (как и изложение используемой математической модели) выходит далеко за рамки цели и объема настоящего сообщения и не является основным предметом сообщения.

Таким образом, решив систему уравнений (3) и получив оценку x ˆ вектора смещений параметров x , нам становится известно, как и какие ОП необходимо «довернуть» или сместить на орбите, чтобы вернуть их в исходное заводское положение, которое соответствует настроенному телескопу.

Если степени свободы неизвестных абсолютных параметров X (определен заглавной буквой ранее) при определении ОП выбрать удобным образом, соответствующим имеющимся актюаторам ОП (например: положение ВЗ задается 6 приводами гексапода, которые могут быть определены как неизвестные компоненты вектора X ), то это дает определенные удобства. В таком случае расчетный вектор смещения x ˆ является вектором, сообщающим, «насколько каждый из приводов ОП смещен от идеального (исходного) положения» и, по сути, сколько необходимо сделать шагов привода, чтобы рассматриваемая ОП «встала» на исходное место. Таким образом, вычисленный вектор x ˆ может быть непосредственным входом для механизмов коррекции ЗС телескопа.

Применение описанного алгоритма настройки телескопа имеет существенные положительные практические качества:

– малость изменений положения ОП позволяет свести задачу к системе линейных уравнений. Это позволяет использовать методы линейной алгебры и дает точное единственное решение обратной задачи с прогнозируемой точностью работы алгоритма;

– нет необходимости знать абсолютные значения параметров x p для ОП;

– нет необходимости точно знать абсолютное положение КМ в системе координат спутника и места установки их на ОП. Не требуется высокой точности установки КМ на панели ГЗ и другие ОП.

3.Численное моделирование работы бортового 3D-сканера с использованием оптических контрольных меток на поверхности зеркальной системы

С целью проведения численного эксперимента, позволяющего моделировать измерения и визуализировать их, было разработано семейство программ на языке Python 3.7 (в среде Anaconda [17]).

Совместно с поверхностями второго порядка, описанными в моделирующем ПО [18], также применяется графическая библиотека VTK [19]. Библиотека VTK применяется для визуализации 3-мерных объектов, которые можно задавать самым общим уравнением поверхности второго порядка, что дает наглядность и возможность визуальной самопроверки закладываемых уравнениями поверхностей ограничений и алгоритмов трассировки лучей в ЗС. Типичный пример генерируемого графического отображения распространения лучей от 3D-сканера через систему поворотных зеркал до обмеряемых КМ отображен на рис. 2.

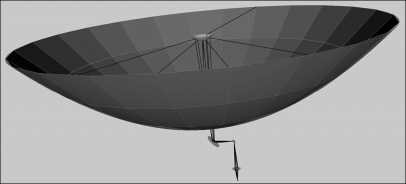
Рис. 2. Пример трассировки лучей к набору КМ: от 3D-сканера до панелей ГЗ

Процесс измерения КМ выполняется численно следующим образом:

• а)    выполняется трассировка (распространение) луча от объектива 3D-сканера СК ЗС, через набор ОП, в направлении к обмеряемой КМ;

• б)    в процессе распространения луча выполняется алгоритм глобальной оптимизации углового положения СЗ 3D-сканера для того, чтобы распространяющийся луч, пройдя весь оптический путь, в итоге попал точно в центр обмеряемой КМ;

• в)    при попадании луча в КМ находятся параметры 3D-сканера, эквивалентные реальному измерению:

• 1)    длина оптического пути по всему пути трассировки луча (измерения дальномерного канала (ДК));

• 2)    угловые положения СЗ 3D-сканера (угломерные каналы измерения).

• 3.1.    Построение дизайн-матрицы, проверка адекватности линейной модели

Для проверки адекватности матричного уравнения y = H × x как модели, связывающей небольшие изменения параметров x ЗС с изменениями в данных обмера, получаемых 3D-сканером y , были решены две задачи численного моделирования:

– построение дизайн-матрицы H по чертежным данным;

– проверка адекватности применения линейной математической модели y = H × x для характеризации поведения телескопа при расстройке его ЗС, характеризуемой вектором x .

В результате использования разработанных алгоритмов программой автоматически строится дизайн-матрица H всей ЗС. Поскольку матрица H считается постоянной, то измерения матрицы выполняются только однократно. Затем посчитанная матрица H со- храняется в файл. Для дальнейших исследований и оценки точностных характеристик модели ЗС достаточно знать только H.

Для проверки адекватности применения линейной модели при характеризации геометрии телескопа проводится следующий численный «точный» эксперимент, выполняющий моделирование обмера:

– моделируется обмер идеально настроенной ЗС телескопа 3D-сканером, с использованием трассировки лучей до всех КМ. Пусть Y – это вектор, описывающий совокупность результатов данных обмера всех КМ 3D-сканером;

– имитируется расстройка ЗС телескопа. Для этого создается случайное отклонение (возмущение) параметров всех элементов ЗС в допустимых техническим заданием пределах, которое обозначим как x ;

– моделируется обмер ЗС телескопа 3D-сканером, с использованием трассировки лучей до всех КМ в условиях расстройки ЗС. Пусть Y – это вектор, описывающий совокупность результатов всех данных обмера всех КМ после внесения возмущения x в ЗC;

– вычисляем вектор изменения обмера в «точном» эксперименте под влиянием возмущения x как: У о = Y - Y .

Таким образом, получено значение изменения положения КМ в координатах 3D-сканера y 0 = f ( x ) как изменения неизвестных параметров x ЗС.

Назовем полученную зависимость y 0 = f ( x ) «точной», «нелинейной».

Теперь сравним результат «нелинейного» моделирования с использованием трассировки лучей y 0 = f ( x ) с результатом, получаемым при помощи ди-зайн-матрицы (линейной модели). Для этого матрич-но умножим (предварительно расчитанную) дизайн-матрицу H на вектор возмущения ЗС x , получим предсказанное моделью изменение обмера КМ:

• У1 = H ■ х.                                              (4)

• 3.2.    Сравнение результатов численного моделирования измерений и линейной модели с использованием дизайн-матрицы

4.    Исследование допустимого разброса параметров ЗС

Сравниваем значение смещения результатов моделирования y 0 со значением смещения y 1 , продуцируемым линейной моделью. Результаты представлены в виде трех графиков. Каждый график соответствует измерениям соответствующего канала 3D-сканера. Дальномерный канал (ДК) 3D-сканера представлен на рис. 3. Два угломерных канала 3D-сканера представлены на рис. 4 и 5.

Как видно из результатов численного эксперимента, матричная модель относительно неплохо предсказывает влияние возмущений ЗС на результаты обмера КМ.

Для определения требований к СК ЗС необходимо оценить максимальные отклонения параметров разных компонентов телескопа от их исходного положе- ния (вторичного зеркала, ПЗ, всех панелей главного зеркала), чтобы луч, попадающий в апертуру телескопа с бесконечности, попадал на выходе из схемы телескопа (в плоскости его изображения, где распо- ложены приемники изображения) в пятно с указанным диаметром:

– 50 мм (после предварительной настройки ЗС);

– 2 мм (после точной настройки ЗС).

О

-2

-4

-6

-8

х

*

X

IL —-

Прямая задача: сравнение точного смещения и линейной модели смещения КМ в дальномерном канале

Sc

хЛ#х ^х

X

* XX

*

х

Р< X X *

х Модельное (дизайн-матрица) смещение расстояния, мм

• Точное смещение расстояния, aim

---Разница между точным смещением и моделью, мм

£—

О        100       200       300       400       500       600       700

Номер (индекс) обмеряемой контрольной метки КМ в зеркальной системе

Рис. 3. Сравнение выхода точного измерения и модели на основе дизайн-матрицы по ДК.

Относительная ошибка модели к формируемой величине (как отношение стандартных отклонений величин) не более 1 %

0,004

0,002

О

-0,002

-0,004

-0,006

Прямая задача: сравнение точного смещения, и линейной модели смещения КМ в угломерном канале 1 ,

х х

х Модельное (дизайн-матрица) смещение угла 1, рад

• Точное смещение угла 1, рад

---Разница между моделью и точной оценкой, рад

О        100       200       300     _ 400       500       600       700

Номер (индекс) обмеряемой контрольной метки КМ в зеркальной системе

Рис. 4. Сравнение выхода точного измерения и модели на основе дизайн-матрицы по угломерному каналу 1.

Относительная ошибка модели к формируемой величине (как отношение стандартных отклонений величин) не более 1,8 %

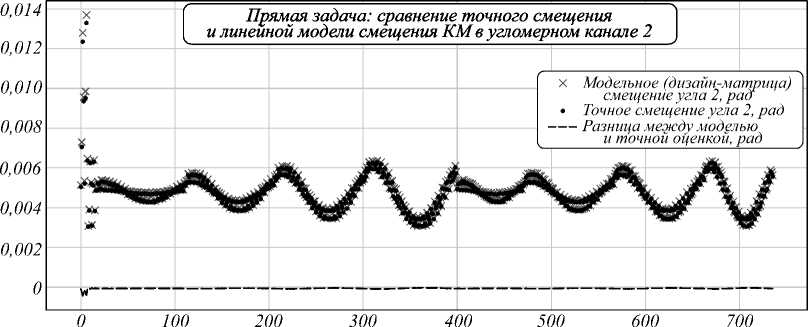
Номер (индекс) обмеряемой контрольной метки КМ в зеркальной системе

Рис. 5. Сравнение выхода точного измерения и модели на основе дизайн-матрицы по угломерному каналу 2. Ошибка модели к формируемой величине (как отношение стандартных отклонений) не более 3 %

Помимо этого, необходимо оценить качество волнового фронта, собираемого телескопом в области изображения, в единицах длины минимальной волны λ ≈ 300 мкм, то есть получить пиковую величину качества волнового фронта λ / k .

Условно, для «хороших» оптических систем при заданной минимальной длине волны λ ≈ 300 мкм полагаем здесь иметь: k ≥ 10 … 30.

Для имитации распространения света рассматриваем распространение луча света по следующим оп- тическим путям: Звезда на бесконечности => Центр панели и ее углы (ГЗ) => Контррефлектор => ПЗ => Плоскость изображения телескопа.

Существуют 4 типа панелей (расположенных на 4 разных ярусах), составляющих ГЗ, поэтому для них будут разные требования к параметрам положения. Требования на параметры положения ВЗ и параметры ПЗ также будут зависеть от того, от какого типа панели (ярус на ГЗ) отразился луч от звезды.

Имеем приблизительно следующую задачу распространения света, как проиллюстрировано на рис. 6.

На рис. 6 изображены 5 параллельных лучей (истекающих из красных сфер параллельно оси ГЗ), имитирующих свет далекой звезды. Лучи звезды попадают в центр панели ГЗ и ее 4 угла, с целью покрыть наибольшие искажения оптического хода света при неправильной установке панели в ЗС. Последовательно отразившись от панели, затем от ВЗ и ПЗ, лучи попадают в плоскость изображения телескопа. В плоскости изображения фиксируется радиальное смещение попадания каждого из лучей от идеального – фокальной точки всей оптической системы. Регистрируется максимальное отклонение волнового фронта (длины оптического пути), а также максимальное отклонение попадания луча от центра изображения.

Этот эксперимент проводится по всем панелям для каждого яруса ГЗ.

Результаты моделирования для формирования изображения звезды в пятне диаметром 2 мм определяют требования к точности измерения положения элементов ЗС в базовой системе координат при эксплуатации на орбите. Эти итоговые требования приведены в табл. 1.

• 5.    Численное моделирование решения обратной задачи. Сравнение оригинального решателя с существующими методами решений уравнений. Проверка качества алгоритмов и формул

Важной задачей является оценка восстановления неизвестного (неявного) вектора x по известным у и H .

Рис. 6. Иллюстрация распространения света по пути: Звезда=>Панель ГЗ=>ВЗ=>ПЗ=> фокальная плоскость изображения

Т.е. необходимо решение обратной задачи 5 с = g ( H , у ) в условиях предположения зависимости у = H х х . Помимо этого, известно, что вектор смещения измерений у на практике не может быть точно известен и содержит шум контрольной аппаратуры.

Решение обратной задачи 5 с = g ( H , у ) сводится к задаче решения системы линейных уравнений с определенными ограничениями и кратко рассмотрено в параграфе 2.

Табл. 1. Расчетные требования к точности контроля положения элементов ЗС в базовой системе координат при эксплуатации

Требование/наименование параметра	Значение	Примечание
Положение ВЗ по координатам Y и Z	≤ 35 мкм
Положение ВЗ по координате X	≤ 66 мкм
По угловым перемещениям ВЗ	≤ 28''	≤ 1,4e–4 радиан
Смещение панелей ГЗ в направлении Y и Z	≤ 35 мкм
Смещение панелей ГЗ в направлении X	≤ 66 мкм
По углу места ПЗ относительно оптической оси	≤ 2,8'	≤ 8,37e–4 радиан, вокруг оси Z
По азимутальному углу ПЗ относительно оптической оси	≤ 2,8'	≤ 8,37e–4 радиан, вокруг оси X
По углу поворота ПЗ вокруг оси Y	≤ 4'	≤ 1,18e–3 радиан

Для проверки основных положений, кратко описанных в параграфе 2, был проведен численный эксперимент, подтверждающий их работоспособность. Он был проверен сравнением оригинального оптимального решателя (см. параграф 2) с двумя классическими способами решения систем линейных уравнений. На входе эксперимента имелась дизайн-матрица H системы, имеющая размерность (2208 × 511), полученная в результате численного моделирования распространения света в телескопе, связывающая смещения КМ и неизвестные изменения параметров в соответствии с уравнением у = H х x . Расчетная дизайн-матрица системы H оказалась крайне близкой к сингулярной с «числом обусловленности» [20] порядка 3 × 10 ⁹ .

Поэтому для решения такой задачи необходимо было искать приближенные решения и использовать ограничения (различные регуляризации).

Численно сравнивалось качество решения уравнения у = H х x с использованием следующих решателей:

• а)    Р1 – оригинальный решатель;

• б)    Р2 – классическое решение методом наименьших квадратов (МНК);

• в)    Р3 – решение с использованием регуляризации (Тихоновская регуляризация с подобранным параметром регуляризации, [21]).

Численный эксперимент проводился следующим образом:

– генерировался случайный вектор отклонения ЗС от исходного положения х, состоящий из 511 параметров смещения (смещения положения всех панелей ГЗ, ВЗ, ПЗ, относительного положения 3D-сканера и др.). Для простоты сравнения использовался одинаковый единичный разброс па- раметров ЗС, что давало необходимую однородность неизвестного вектора x;

– имитировался реальный контроль параметров ЗС: для этого вычислялось смещение КМ по модели y = H × x , к которому добавлялся шум измерения каналов 3D-сканера СК ЗС. Вектор измерений состоял из 2208 значений (все каналы 3D-сканера по всем КМ);

– по вектору зашумленного измерения y каждым решателем (Р1, Р2, Р3) восстанавливалось смещение ЗС как: x 1 (Р1), x 2 (Р2), x 3 (Р3);

– вычислялась погрешность восстановления параметров x как вектора ε1 = x 1 – x (для Р1), ε2 = x 2 – x (для Р2), ε3 = x 2 – x (для Р3).

Эксперимент повторялся в цикле 100 раз, и накапливалась статистика ошибок восстановления каждого из параметров x для каждого из решателей. По каждому из параметров x для каждого из решателей было вычислено (на 100 экспериментах) среднеквадратичное значение ошибки (СКО). На рис. 7, 8 представлено сравнение шума восстановления параметров тремя решателями.

Из результатов моделирования, представленных на рис. 7 и 8, следует, что разработанный метод Р1 имеет точность существенно выше (СКО практически на порядок ниже), чем стандартные методы решений линейных уравнений (МНК, Тихоновская регуляризация с подобранным параметром регуляризации) применительно к решению уравнения y = H × x для ЗС телескопа, поэтому он предпочтителен в данной работе. Численными экспериментами доказана работоспособность Р1.

СКО, усл.ед.

103Г----

ю-С

KM

j CKO восстановления вектора ,r Д

---Pl. оптимальный решатель P2. MHKрешатель

— РЗ. Тихонов, X=L2 ________

ЮС

10= ■

IOC

IO"2, lO'C

10"4\

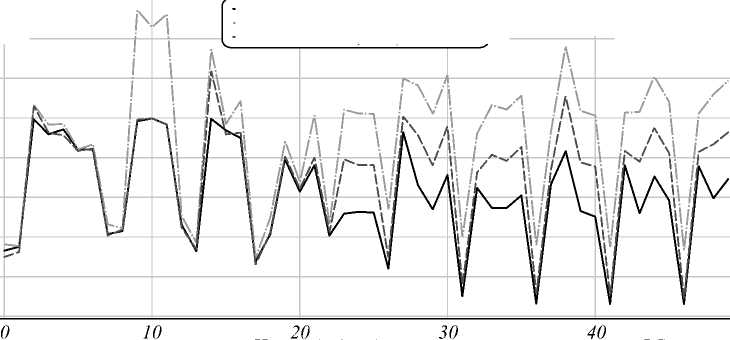
Номер (индекс) восстановленного параметра ЗС в векторе х

Рис. 7. СКО восстановления параметров x (на выборке из 100 тестов) только для первых 50 параметров вектора x

Г СКО восстановления вектора х ]

CKO, усл.ед.

103i

102:

° Pl. оптимальный решатель + P2. MHKрешатель

, x РЗ. Тихонов, X=l,2

lOh

IOC

++ Х^+ .

, X

10"C

^”/хХ_?1< ХХ^^ХХ» ,Х„,ЛУ>

X

X

X хЖ

• V.X .   *

IOC

10-K

*x

X

X •

10"C

X

X

X х х х х

x

10-Ц

• • х х .

X

x

X

X X

X 2 •

X *

X X X.

Номер (индекс) восстановленного параметра ЗС в векторе х

Рис. 8. СКО восстановления параметров x (на выборке из 100 тестов) для всех параметров вектора x. Единицы оси ординат – безразмерные

Дополнительно были проверены выводы модели, предсказывающие точность Р1. Рис. 9 демонстрирует сравнение СКО метода Р1 и предсказание СКО Р1 по формулам модели.

Как видно из рис. 9, формула СКО оптимального решателя работает корректно. Следовательно, можно сделать основные выводы:

• а)    все формулы для восстановления смещений параметров ЗС, полученные в нашей модели, рабочие, и их можно применять на практике и в разработке ПО космической обсерватории;

• б)    необходимость длительных вычислительных экспериментов при исследовании эффективности моделей (для различных конфигураций располо-

  жения КМ) отпадает, так как качество алгоритма может быть точно предсказано.

  
  

  СКО, усл. ед.

  
  

  10°-у юн юн юн Ю'Ь 10"⁵-

  
  

  рх

  
  

  *

  
  

  X

  
  

  X

  
  

  х х

  х Ххх х _{х х}

  
  

  X

  
  

  x Pl. оптимальный решатель ~

  • Оценка СКО по предложенной формуле

  
  

  J CKO восстановления вектора x

  
  

  X

  
  

  x

  
  

  ж

  
  

  Хх

  
  

  ^ X

  
  

  X X^х

  
  

  ^Х     X X   X

  х xj^Xx _хх _х

  
  

  X

  ^Х х ^ X

  
  

  ^ж X X ж _w

  
  

  -^

  Ж Xv

  К ЖЖ *

  
  

  ^^ хх^Ч^{хХх        Х}

  ^^^М*^ ^’^’Ч^х J^⁶*

  
  
  
  

  X

  
  

  Х>*_хх

  
  

  X

  
  

  X

  **

  • ж ж

  ж

  
  

  ж X жжж

  
  

  ж

  
  

  ж ж

  
  

  ж

  
  

  ж

  
  

  ж

  
  

  'X^х

  ж хх >0<$yx**V”

  X Хх X** *

  ж

  ж

  

  ж

  Хк* X хх х X

  хХх ^^ х^х^хх

  
  

  ж

  
  

  * X

  
  

  ж х*

  
  

  X * Ж ж^х X ж ж

  
  

  ж ж

  
  

  X

  *

  
  

  Хж ЖЖ

  
  

  хж

  
  

  X X

  
  

  Хх х"^

  
  

  200           300           400            500

  Номер (индекс) восстановленного параметра ЗС в векторе х

  
  

Рис. 9. Сравнение СКО оптимального решателя, полученной в численном эксперименте, с результатами аналитической формулы СКО оптимального решателя

Заключение

Создан не имеющий аналогов метод предварительной оценки смещения элементов ЗС телескопа по косвенному (неявному) контролю, выполняемому 3D-сканером.

Метод основан на математическом преобразовании косвенных измерений отклонений y положения КМ ЗС телескопа от их эталонного положения, на выходе которого выдается список оценок смещений неизвестных параметров x элементов ЗС, задаваемых удобным образом (например, пространственное положение, положение исполнительных механизмов, определение формы ОП).

Этот метод универсален и применим к любым сложным конструкциям (и функциональным зависимостям), претерпевающим небольшие отклонения от идеальной формы. Поэтому метод применим к многомерным системам любого вида (обмеряемым не только оптическими средствами, но и произвольными неявными зависимостями). Обмеряемые и восстанавливаемые величины могут быть произвольной природы. Например, метод вполне может быть использован в дальнейших работах с крупногабаритными трансформируемыми конструкциями и сложными условиями их обмера, что типично для космических антенн и иных протяженных, сложных и труднодоступных объектов со сложными многомерными взаимодействиями.

Создан набор математических формул, позволяющий оптимально решать обратную задачу на основе системы линейных уравнений для восстановления многомерных параметров объекта по многомерным косвенным измерениям, в условиях вероятностного разброса параметров и произвольных данных о типе, каналах и о шумах контрольной аппаратуры.

Показана возможность контроля параметров ЗС телескопа с целью его предварительной настройки при использовании 3D-сканера на борту КА. Вычислены пределы допустимых отклонений компонент ЗС, необходимые для обеспечения функциональности телескопа.

Созданы оригинальные практические алгоритмы как основа для решения подобных задач моделирования в будущих работах.

Работа выполнена при поддержке Министерства науки и высшего образования РФ в рамках выполнения работ по Государственному заданию ФГБУН КТИ НП СО РАН в части проекта АААА-А 20-120102190007-5 .