Математическое моделирование работы поворотной винтовой колонки бурового судна при его произвольном движении

Буровое судно, работая в режиме динамического позиционирования (ДП), перемещается по произвольной траектории, существенно отличающейся от прямолинейной. При этом значения параметров, определяющих гидродинамические условия работы поворотных винтовых колонок (ПВК), изменяются по отношению к значениям аналогичных параметров, соответствующим его установившемуся прямолинейному движению.

2.    Моделирование кинематических параметров потока

Скорости потоков, натекающих на правую (s) и левую (p) ПВК, определяются зависимостью

υ′e(s,p) = υnp(s,p)(1 – ψ′), где υnp(s,p) – линейная скорость бурового судна в месте установки конкретного ПВК, ψ′ – коэффициент номинального попутного потока в месте установки ПВК при произвольном движении бурового судна. Значение υnp(s,p) зависит от кинематических параметров движения судна, а именно угла дрейфа судна β и линейной скорости υ, а также угла дрейфа в месте установки ПВК βnp(s,p), т.е.

υ np ( s , p ) = [cos β / (cos β np ( s , p ) )] υ .                                         (2)

В свою очередь, величина угла дрейфа в месте установки ПВК β np ( s , p ) определяется по формуле:

β np ( s , p ) = arctg 〈 {tg β – [ x np ω /( υ cos β )]}/{1 – [ y np ( s , p ) / ( υ cos β )]} 〉 ,                (3)

где x np , y np ( s , p ) – координаты места установки ПВК, ω – угловая скорость судна.

Коэффициент номинального попутного потока в районе расположения ПВК ψ′ при произвольном движении бурового судна определяется исходя из рекомендаций, представленных в работе ( Гофман , 1988):

ψ ^′ = ψ ∙г [( β np ^lim – β np ( s , p ) )/ β np ^lim ] ⁵ при β np ( s , p ) ≤ β np ^lim ;

ψ = ψ t 0 при βnp(s,p) > βnplim, здесь значение угла дрейфа βnplim, при котором номинальный попутный поток становится нулевым, по результатам анализа многочисленных модельных экспериментов, принимается равным βnplim = 45°.

Угол, определяющий направление потока, натекающего на ПВК, в математической модели задаётся зависимостью

β np ( s , p ) ⁼ к β np ( s , p ) ^.

Для определения значения коэффициента скоса потока κ , учитывающего искажение направления натекания воды на ПВК вследствие влияния корпуса, используется зависимость, полученная на основании результатов анализа материалов экспериментов ( Гофман , 1988)

κ 0 + (1 – κ 0 )∙( β np ( s , p ) / β np ^lim ) ⁵ при β np ( s , p ) ≤ β np ^lim ; 1 при β np ( s , p ) >  β np ^lim .

Вестник МГТУ, том 13, №4/2, 2010 г.   стр.852-856

Начальное значение коэффициента скоса потока κ 0 для бурового судна принято равным: для ПВК внутреннего борта κ 0 = 0.7; для ПВК внешнего борта κ 0 = 0.9.

С учётом представленных изменений в характере потока, натекающего на ПВК, относительная поступь принимает следующее значение

λ ′ е = υ ′ е / nD ,

где D – диаметр винта; n – обороты винта.

3.    Моделирование гидродинамических характеристик ПВК

Величине λ ′ е соответствуют изменённые по сравнению с номинальными диаграммные значения коэффициентов упора ПВК К ′ _np и винта, работающего в составе ПВК, К ′ _р и соответствующие им расчётные значения упоров Т ′ np , Т ′ р , учитывающие лишь те изменения в режиме работы ПВК, которые связаны с изменением скорости υ ′ е потока, натекающего на ПВК. Они не учитывают влияния на режим работы ПВК ни угла её поворота, ни направления потока, натекающего на ПВК, и поэтому называются условными. Для определения величин К ′ np , К ′ р , Т ′ np , Т ′ р и их соотношений используются те же диаграммы и зависимости, которые использовались для определения их значений при прямолинейном движении бурового судна ( Юдин , 2010). Так, например, при использовании в расчётах результатов экспериментальных исследований, выполненных В.К. Турбаллом, зависимость, используемая для определения значения коэффициента упора ПВК, в данном случае будет выглядеть следующим образом:

К ′ np = -0.0404( λ ′ е ) ² – 0.4526 λ ′ е +0.4474.                               (8)

Другая группа изменений в режиме работы движителя при произвольном движении бурового судна связана с изменением угла натекания воды на ПВК (местного угла дрейфа β ^* _np ) и с изменением взаимодействия движителя со средствами управления вследствие поворота ПВК на заданный угол δ np при неизменных значениях υ ′ e , ψ ′ и оборотов винта n .

Для численной оценки этих изменений вводятся коэффициенты t_np , t_p , характеризующие изменения упора ПВК и упора гребного винта, вызванные косым натеканием и поворотом ПВК.

t np = Т ^r np / Т ′ np = K ^r np / K ′ np ;

t p = Т ^r p / Т ′ p = K ^r p / K ′ p .

Здесь верхний индекс " r " означает, что данное значение указанного параметра соответствует реальным условиям работы ПВК (в данном случае под термином "реальные условия" подразумеваются условия обтекания ПВК при произвольном движении бурового судна).

Коэффициенты t np , t p являются функциями угла перекладки ПВК δ np , угла скоса потока β ^* np и условного коэффициента нагрузки ПВК по упору σ ′ np .

Определение режима работы ПВК при известных параметрах произвольного движения бурового судна ω , β , υ , ψ ′ и оборотов винта n производится в два этапа: определяются кинематические и динамические характеристики условного исходного режима работы ПВК λ ′ е = υ ′ е / nD ; К ′ np ( λ ′ е ); К ′ p ( λ ′ е ), а затем с учётом значений коэффициентов t np , t p определяются значения гидродинамических характеристик работы ПВК в реальных условиях

K

r np

= t_np K ′ _np ;

K ^r p = t p K ′ p ;

T ^r np = K ′ np ρ n ² D ⁴ ;     T ^r p = K ′ p ρ n ² D ⁴ .

Таким образом учитывается влияние корпуса бурового судна на гидродинамические характеристики работы ПВК при произвольном движении.

В то же время, в математической модели бурового судна необходимо учитывать влияние работающего ПВК на характер обтекания корпуса, проявляющееся в образовании на последнем известной силы засасывания ∆ T , которая в случае произвольного движения раскладывается на две составляющих: продольную Х ∆ T и поперечную Y ∆ T .

Продольная составляющая силы засасывания приводит к увеличению нагрузки на ПВК ( Юдин , 2010), не оказывая влияния на характер движения бурового судна.

Поперечная сила засасывания Y ∆ T , при произвольном движении бурового судна, может быть отнесена к поперечной составляющей гидродинамической силы на корпусе судна ( Гофман , 1988).

В этом случае поперечная составляющая гидродинамической силы, образующейся на корпусе бурового судна при его произвольном движении под воздействием работающего ПВК, и её момент будут определяться по формулам:

Y k ^r = k y Y k ;                                                  (10)

M k ^r = k y k cp M k ,                                     (11)

где ky – коэффициент изменения силы на корпусе бурового судна при работе ПВК; kcp – коэффициент смещения центра давления на корпусе при работе ПВК, Yk, Mk – поперечная составляющая и момент гидродинамической силы на корпусе судна, соответственно, без учёта взаимодействия с работающей ПВК.

Коэффициенты динамического взаимодействия k y , k_cp связаны сложными соотношениями с кинематическими параметрами движения бурового судна to , в и зависят от режима работы его ПВК. При угле дрейфа в > 15 ° их значения могут быть приняты постоянными, т.е. k y = 1.2, k_cp = 0.8 ( Гофман , 1988). При малых углах дрейфа в < 15 ° значения коэффициентов k y , k_cp принимаются равными 1.0.

Гидродинамические характеристики ПВК, основными элементами которой являются гребной винт и направляющая насадка, обладают рядом специфических особенностей, связанных с работой насадки в косом потоке.

При работе ПВК в косом потоке насадка формирует поле скоростей перед гребным винтом, выравнивает его и делает практически совпадающим по направлению с осью гребного винта, сохраняя величину скорости натекания. В результате скос натекающего на ПВК потока мало влияет на величину упора её гребного винта Т р . В математической модели бурового судна с учётом данных, полученных по результатам анализа модельных экспериментов ( Muller , 1981), в диапазоне местных углов дрейфа 0 ° <  в np <  90 ° , принято для ПВК t p = 1. Это значение близко к реальному значению при работе ПВК в швартовном режиме, который является характерным для бурового судна.

При тех же значениях углов натекания потока на ПВК (0 ° <  в * _np <  90 ° ) и при работе последнего в режиме достаточно близком к швартовному, коэффициент t_np лежит в диапазоне 1,05 <  t_np <  1,10 ( Muller , 1981), при моделировании его значение принято равным t_np = 1,10.

4.    Моделирование образования реактивной силы и её составляющих

Известно, что движущей реактивной силой, действующей на работающую ПВК, является так называемая результирующая сила R , образующаяся в результате сложного характера обтекания ПВК, представляющей комплекс, состоящий из гребного винта и насадки.

Значение результирующей силы, действующей на ПВК, в математической модели бурового судна рассчитывается по методу, предложенному А.Д. Гофманом (1988) с использованием результатов модельного эксперимента, выполненного в Дуйсбургском опытовом бассейне ( Muller , 1981).

Для определения значения результирующей силы при произвольном движении бурового судна и с учётом режима работы ПВК обратимся к рис. 1. На рис. 1 показаны основные геометрические параметры, определяющие положение ПВК относительно корпуса судна и направления набегающего потока при произвольном движении бурового судна и заданном угле поворота ПВК 8 _np , а также вектор результирующей силы и её составляющие в координатной системе, связанной с судном.

Для определения значения результирующей силы R используются результаты уже упомянутого здесь модельного эксперимента ( Muller , 1981). На основании их А.Д. Гофманом (1988) предложена зависимость отношения результирующей силы к упору ПВК T np при осевом натекании потока ( 8 _ep = 0)

t R = R / T np ⁰ (12)

от значения реального угла 8 _ер и коэффициента нагрузки ПВК по упору о ° _пр в осевом потоке, при скорости натекания U _e , рассчитанной по формуле (1), исходя из условия в np ( _sp ) = 8 _np ( _sp ) и частоте вращения гребного винта n .

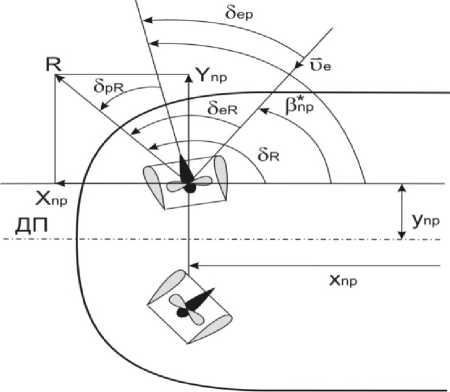
8R - угол отклонения вектора результирующей силы от оси OnpXnp координатной системы OnpXnpYnp (подвижная, прямоугольная правая координатная   система, связанная с судном, начало координатной системы Опр совпадает с точкой расположения ПВК, положительное направление оси OnpXnp - в нос судна, положительное направление оси OnpYnp - на левый борт);

8 _ep — угол между вектором скорости потока и' e , натекающего на ПВК и осью гребного винта, положительное направление которой совпадает с направлением вектора результирующей силы;

8 _eR - угол между вектором скорости потока, натекающего на ПВК и вектором результирующей силы;

8 _pR - угол между осью гребного винта и вектором результирующей силы, положительное направление отсчёта углов 8 _ep , 8 _eR , 8 _pR - против часовой стрелки.

При этом ось гребного винта ПВК считается направленной в сторону, противоположную отбрасываемой винтом струе.

Рис. 1. Схема углов и сил на ПВК

Вестник МГТУ, том 13, №4

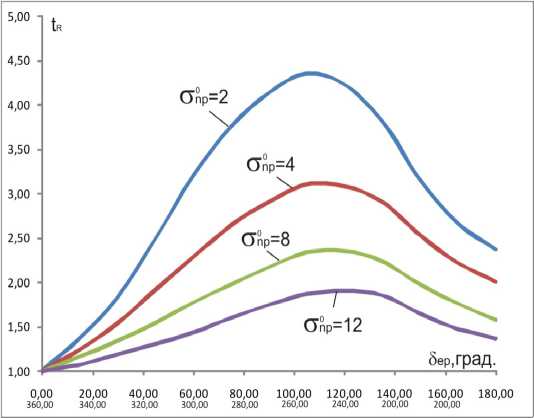
Рис. 2. Зависимость коэффициента t R от угла натекания потока S _ep и коэффициента нагрузки по упору при осевом натекании потока на ПВК О _пр

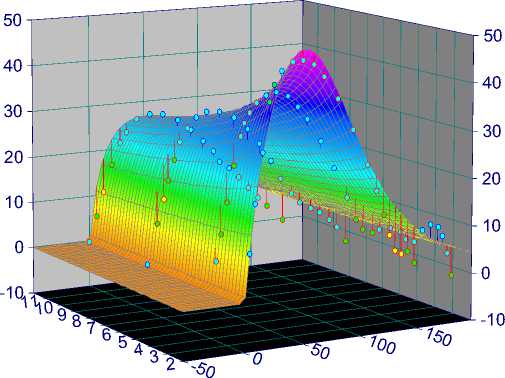
Рис. 3. Угол отклонения результирующей силы ПВК от оси гребного винта S _pR( S ep , О 0 _пр )

Зависимости t_R( S _ep, О _пр ), S _pR( S _ep, О _пр ) для испытанной серии гребных винтов В4-55, работающих в насадке, в графическом формате приведены на рис. 2, 3 (значения угла S _ep в диапазоне 180 ° <  S _ep <  360 ° (рис. 1) должны приниматься отрицательными).

Аналитическое выражение представленных в графическом виде зависимостей выглядит следующим образом:

t R = { S ep O пр /[ a + b S ep + d o ⁰ пр + e ( О пр ) ² + / д ер ³ + g ( О пр ) ³ ]}/( h S ep O пр );          (13)

S pR = { a + b S ep + c S ep ² + d S ep ³ + e / S ep + /exp(- S ep ) + ln( o° пр )•[ g ( О пр ) ^0,5 + h ]} ^-1 .      (14)

Численные значения коэффициентов, входящих в формулы (13), (14) представлены в таблице.

Таблица

Коэффициент	Значение
	формула (13)	формула (14)
a	144800,38	0,0017734075
b	3149,932	0,00018423491
c	-26127,25	-3,3856374 х 10 -6
d	-21,65865	3,9239205 х 10 -8
e	2601,4726	0,3 8410829
f	0,0339983	1,1724215
g	-98,26864	0,0008596628
h	-0,00000488	0,0059520227

Гидродинамические характеристики ПВК, ось которой расположена под углом S _ep к вектору скорости натекающего на ПВК потока, моделируются в соответствии с представленным ниже алгоритмом.

Используя выражение (5) и учитывая, что для отдельно взятого ПВК угол дрейфа в районе его установки будет определяться зависимостью

З пр ( 5 , р )    к ^S np ( 5 , р ) ,

определяем значение скорости натекающего на ПВК потока U е . С учётом полученного значения U е , а также текущего значения частоты вращения гребного винта ПВК п рассчитывают относительную поступь X е = U е / nD . Значение коэффициента упора ПВК при осевом натекании потока ( S _ep = 0) K_np определяем на основании полученной ранее зависимости, например,

K np = -0,0404( X' e ) ² - 0,4526 X' е + 0,4474.

Исправляем это значение, учитывая влияние кронштейна и гондолы ПВК на работу комплекса "винт — насадка", пользуясь выражением

K npn = K np { К п [1 — 1/(1+ t n )]+ K p /(1+ t n )},                          (17)

которое получено с использованием зависимостей, представленных в работе ( Юдин , 2010).

Далее находим значение упора ПВК 7°_пр при осевом натекании:

T 0 np = K npm p n 2 D 4 .

Определяют коэффициент нагрузки ПВК по упору при осевом натекании : o ° np = (8/ л )[ K npn ( X е ) ² ].

Угол натекания потока на ПВК определяется в виде зависимости (рис. 1) ^S ep ^S np ^в np ( s , p ) .

Используя зависимость (13), с учётом полученных значений S _ep и о°_np , находят величину коэффициента t R (при работе ПВК в швартовном режиме значение t R принято равным единице t R = 1,0), а значение угла отклонения силы R от оси вала гребного винта ПВК S _pR определяем по формуле (14).

Величина результирующей силы R , действующей на ПВК, будет равна

R = t R T ⁰ np .

Определив угол отклонения результирующей силы R от направления натекающего на ПВК потока

S eR = S ep + S pR ,

рассчитывают упор ПВК Т np и нормальную силу Y p (вектор силы направлен перпендикулярно оси гребного винта):

T np = R cos S pR , Y p = R sin S pR .

У ПВК отклонение результирующей силы R от оси гребного винта имеет достаточно значение (рис. 3), поэтому в определённых режимах работы ПВК оно учитывается математическом моделировании.

С учётом скоса потока угол натекания воды на ПВК (рис. 1) имеет следующее значение

^S ep ^S np ^{— в} np ( s , p ) -

большое при её

Параметры работы ПВК бурового судна при текущем значении угла натекания S ep , скорости натекания и'_e и частоте вращения гребного винта n находят так же, как и для изолированного ПВК (при отсутствии корпуса судна).

Угол отклонения результирующей силы R от оси O np X np (рис. 1) определяется из выражения:

S r = S np + S pR ,

поперечная сила, образующаяся в результате работы ПВК бурового судна при его произвольном движении, в координатной системе O_npX_npY_np рассчитывается с использованием зависимости

Y np = R sin S R = t R T np sin( S np + S pR ),                          (27)

продольная сила в указанной системе координат

X np = R cos S r = t R T ⁰ np sin( S np + S pR ).                         (28)

Значения S _pR в диапазоне углов 180° <  S ep < 360 ° (рис. 1) принимаются отрицательными.

5. Заключение

Представленная в статье математическая модель расчёта динамических характеристик работы ПВК при его произвольном движении использована автором для создания математической модели бурового судна, оборудованного движителями рассмотренного типа. Результаты моделирования работы бурового судна в режиме динамического позиционирования в сравнении с результатами натурного эксперимента позволяют считать разработанную модель вполне адекватной. По мнению автора, данная модель может быть использована в соответствующих тренажёрных системах.