Математическое моделирование распространения радиоволн в ионосфере земли в зависимости от высоты источника излучения

рий в изотропной, неоднородной, нестационарной средах бихарактеристическая система уравнений с гамильтониано2м

Г= k x + Ц + к² - е(Г, к,го) ⁽¹⁾

имеет вид [4]:

dr = дГ dk = — дГ dt = дГ dro сдг (2) dT дк’ dT дг’ dT дго dT дt’ где r = (x, y, z) - координаты точки наблюдения, к = (kx, ky, kz) - волновой вектор, го - круговая частота излучения, t - групповое время, г - параметр вдоль лучевой траектории, е(Г, к, го) -эффективная диэлектриче ская проницаемость среды распространения, с = 2,997925-108 м/с -скорость света.

Системы (1-2) (см. [5]) обобщают бихарак-теристическую систему, использованную в [4] для лучевого описания распространения стационарного сигнала в ионосфере. Эффективная диэлектрическая проницаемость среды для неоднородной изотропной ионосферы имеет вид (см., например, [11; 12]):

Е = 1 -V .                                       (3)

Параметр v обозначает отношение квадрата плазменной частоты к квадрату рабочей частоты:

-

4 ne2 N me

- Р

^V = -’

ции нижнего слоя по отношению к основному, z ₀₂ – высота максимума нижнего слоя E , z_{m 2} – условная полутолщина нижнего слоя E , N ₀ – электронная концентрация в максимуме основного слоя F 2, если в - 0 .

где e = 4,8029·10^–10 СГСЭ – заряд электрона, m_e = 9,108·10^–28 г – масса электрона, N – величина электронной концентрации в фиксированной точке пространства.

Предположим, что начальный волновой вектор k (0) параметрически зависит от углов выхода луча α ₀:

k x (0) = - c

ЕЕ^{0 8} а ₀ , k y ⁽⁰⁾ - 0,

- kz (0)- — V Ео sin ао,                            (5)

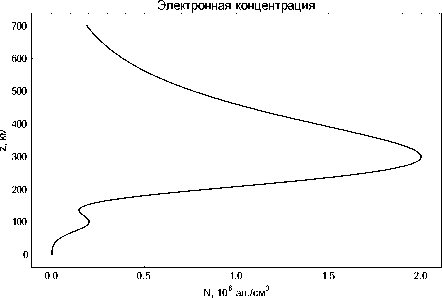
Рис. 1. Профиль электронной концентрации

источник излучения – точечный, находится вне магнитоактивной плазмы и расположен в начале координат ( x ₀ , y ₀ , z ₀), где x ₀ = y ₀ = 0:

^Fl t - 0 = ⁽ x 0 ’ У 0 ’ z 0 ).                                   ⁽⁶⁾

Величина ε ₀ в выражениях (5) – это значение эффективной диэлектрической проницаемости среды в источнике.

Предположим, что сигнал – линейно частот-но-модулированный (ЛЧМ), то есть формула для мгновенной частоты заполнения имеет вид [5]:

- (0) - - 0 (1 + Sn ), t (0) - n               (7)

f (t) - f, (1+St), 5=^fgy, f 0 Tu где n - начальное время выхода луча, f0 - начальная частота (Гц), fд – девиация частоты (Гц), Tи –длительность импульса (с). В данной работе были приняты следующие значения параметров f0 = 3,5 МГц, fд = 56 кГц, Tи – 32 мс.

Предположим, что распространение электромагнитной волны изначально осуществляется в плоскости ( x , z ). Модель ионосферной плазмы двухслойная, а профиль электронной концентрации имеет вид [4; 9; 12] и представлен на рис.1:

1 Г        exp (- ^)

exp- 1 - О --+

2        cos х

При вычислении применялись следующие значения параметров: N ₀ = 2·10⁶см ^{- 3}, Н ₀ = 0,36 Э , Z_{m 1} = 140 км , Z ₀₁ = 300 км , Z_{m 2} = 40 км , Z ₀₂ = 100 км ,

ВЕСТНИК 2016

N ( r ) - N 0 '

а)

z, км 200

x, км

+ в exp

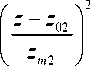
z ^- z 01

^z m 1 ^{2 ,}

б)

где z ₀₁ – высота максимума слоя F 2, z_{m 1} – условная полутолщина слоя F 2, β – безразмерный ко-

эффициент, характеризующий степень иониза-

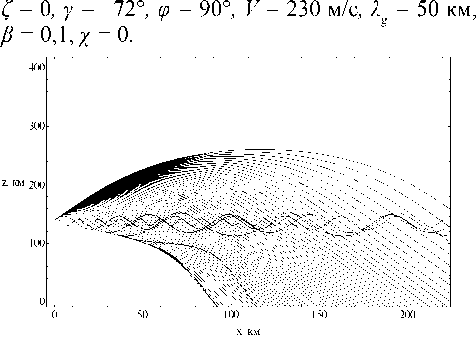
На рисунках 2а и 2б показаны лучевые структуры ЛЧМ радиосигнала в случае распространения в плоскости ( x, z ) при высоте источника

излучения 140 км. Углы выхода лучей 65° и 80° соответственно. Имеет место волноводное распространение в ионосферном межслоевом волновом канале. Сравнивая рисунки, находим что с увеличением угла выхода более высокие частоты начинают проходить ионосферные слои, а более низкие частоты отражаются в сторону Земли.

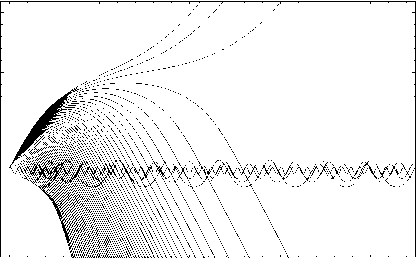
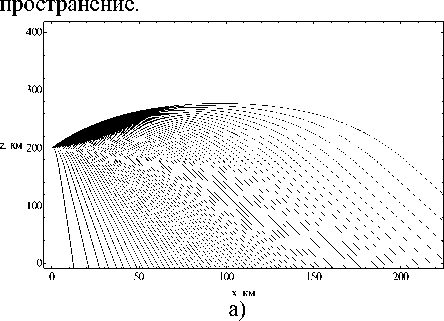
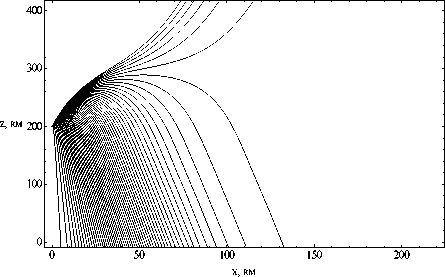
На рисунках 3а и 3б показана лучевая структура ЛЧМ радиосигнала в случае распространения в плоскости ( x, z ) при высоте источника излучения 200 км под углом 65° и 80° градусов соответственно. Сравнивая рисунки, видим, что при увеличении высоты источника излучения количество лучей, проходящих ионосферные слои, увеличивается и исчезает волноводное рас-

ВЕСТНИК 2016

б)

Рис.3. Лучевые структуры ЛЧМ радиосигнала при высоте источника излучения z ₀ =200 км

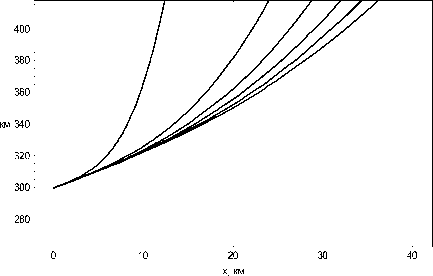
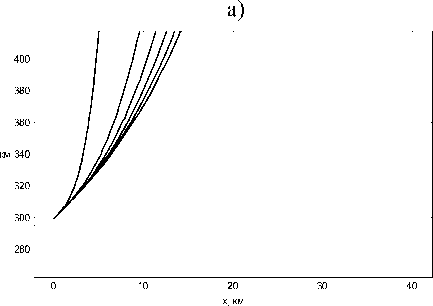
На рисунках 4а и 4б показана лучевая структура ЛЧМ радиосигнала в случае распространения в плоскости (x, z) при высоте источника излучения 300 км под углом 65° и 80° градусов соответственно. Хорошо видно, что при большой высоте источника излучения все лучи проходят ионосферные слои. Отметим существенно меньшее количество лучей, вышедших из источника в данном случае. При рассмотрении формулы (4) и рис. 1 видно, что при больших значениях электронной концентрации на высоте 300 км на большинстве рассматриваемых частот параметр ν становится > 1, вследствие чего нарушается условие выхода волны из источника, и мы видим только те лучи, частота которых удовлетворяет условию ν < 1 (т.е. самые высокочастотные компоненты сигнала).

б)

Рис. 4. Лучевые структуры ЛЧМ радиосигнала при высоте источника излучения z ₀ = 300 км

Таким образом, в проделанной работе сопоставлены особенности распространения ЛЧМ сигналов в двухслоевой изотропной ионосфере при отсутствии горизонтальных градиентов на различной высоте и различных углов выхода. Для расчетов лучевых характеристик применялась бихарактеристическая система дифференциальных уравнений, неизвестными в которой являются не только координаты луча и компоненты волнового вектора, но также частота и время. Были выявлены следующие закономерности:

– при увеличении угла выхода лучей, частоты сигнала и высоты источника излучения количество отраженных лучей сокращается, а прошедших ионосферные слои – увеличивается;

– при некоторой высоте источника, фиксированном угле выхода и неизменных параметрах ЛЧМ сигнала все лучи проходят ионосферные слои.

В дальнейшем при изучении распространения ЛЧМ сигналов в изотропных средах необходимо рассчитывать электромагнитные поля со сложной каустической структурой. Для подобных расчетов применяют метод канонического оператора Маслова [11; 13] и волновую теорию катастроф [14–16]. Также для описания распространения ЛЧМ сигналов в ионосфере желательно строить динамические модели [17], используя восстановленные по данным радиотомографии [7; 18] профили электронной концентрации и различные модели магнитного поля Земли [19].