Математическое моделирование распространения радиоволн в нестационарной плазме с учетом кривизны поверхности Земли и ионосферных слоев
Автор: Крюковский Андрей Сергеевич, Скворцова Юлия Игоревна
Рубрика: Математическое моделирование
Статья в выпуске: 1-2, 2016 года.
Бесплатный доступ
На основе бихарактеристической системы уравнений в сферической системе координат выполнено математическое моделирование распространения радиоволн декаметрового диапазона в нестационарной ионосфере с учетом кривизны поверхности Земли и ионосферных слоев. Рассмотрено распространение обыкновенной и необыкновенной электромагнитных волн в условиях быстрого образования спорадического слоя, построены проекции лучей и компонент волнового вектора в сферической системе координат, исследованы зависимости частоты сигнала от группового времени и широты.
Бихарактеристики, моделирование, обыкновенная волна, необыкновенная волна, распространение, каустики, волновые катастрофы, групповое время, нестационарная ионосфера
Короткий адрес: https://sciup.org/148160247
IDR: 148160247 | УДК: 537.87
Текст научной статьи Математическое моделирование распространения радиоволн в нестационарной плазме с учетом кривизны поверхности Земли и ионосферных слоев
Настоящая работа посвящена распространению радиоволн декаметрового диапазона в ионосфере Земли. В отличие от [1–11], в данной работе учтена кривизна поверхности Земли и ионосферных слоев. Рассмотрена нестационарная модель однослоевой ионосферы, в которой предусматривается образование за очень короткое время (несколько долей секунды) дополнительного спорадического слоя:
N ( г ) = N 0 < exp
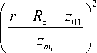
+ p t exp
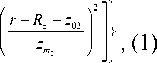
где N 0 – электронная концентрация в максимуме слоя F2 в начальный момент времени, z 01 – высота максимума слоя F2 над поверхностью Земли, zm – условная полутолщина слоя F2, β – коэффициент, характеризующий скорость ионизации спорадического слоя, z 02 – высота максимума спорадического слоя, zm – условная полутолщина спорадического слоя, Rz – радиус Земли. В данной работе рассматривается распространение радиоволн в сферической системе координат, связанной с декартовой соотношениями:
x = r sin 9 cos ф
< y = r sin ^ sin ф . z = rcos 9
Здесь и декартовая, и сферическая системы координат привязаны к центру Земли. В формулах (2) r – расстояние от центра Земли до точки наблюдения, ф - долгота, а 9 = -9 s + п / 2, где 9 s -широта (знак «+» – северная, знак «–» – южная). При выполнении расчетов предполагалось, что: N 0 = 2 10 6 см - 3 , z m = 100 км, z 01 = 300 км, z m = 10 км, z 02 = 200 км, Rz = 6378 км, в = 100.
Известно (см., например, [1; 7–11]), что эффективная диэлектрическая проницаемость в анизотропной плазме имеет вид:
е ± = 1 -
2 v (1 - v )
2(1 - v ) - u sin2 a ± Au 2 sin4 a + 4 u (1 - v )2 cos2 a
, (3)
где знак «+» соответствует обыкновенной волне, а знак « - » - необыкновенной. В формуле (3) введены обозначения:
4 п е 2 N ( r ) m e m2
- величина, пропорциональная квадрату плаз- менной частоты, и u=
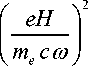
- величина, пропорциональная квадрату гирочастоты. В выражениях (4) и (5) го = 2 nf - круговая частота, с = 2,997925 10 10 см/с – скорость света, e = 4,8029 10 -10 СГСЭ – заряд электрона, me = 9,108 10 –28 г – масса электрона, Н – величина магнитного поля Земли.
Входящий в формулу (3) угол а между внешним магнитным полем Земли H и волновым
—►
вектором k определяется как
cos 2 a =
( H x k x + H y k y + H z k z ) 2
H 2 k 2
Собственно знание величины угла излишне. Для формулы (3) достаточно знать квадрат косинуса этого угла. В настоящей работе предполагалось, что амплитуда магнитного поля постоянная (Н = 0,36 Э), а ориентация напряжённости магнитного поля относительно локальной системы координат задается двумя постоянными углами γ и ψ:
Hx = H cos у cos ^ , H y = H cos y svn v ,
H z = H sin у . (7)
При вычислениях предполагалось, что
Y = 45 ° , у = 90 ° .
Известно (см., например, [6]; также [2–5]), что для построения лучевых траекторий в про- извольной ортогональной системе координат бихарактеристическая система уравнений с гамильтонианом [12]:
3 p 2 m 2
r= E j f —г е ( t, m , q , p ) (8)
j=1 h, c имеет вид:
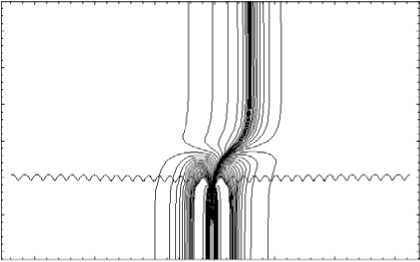
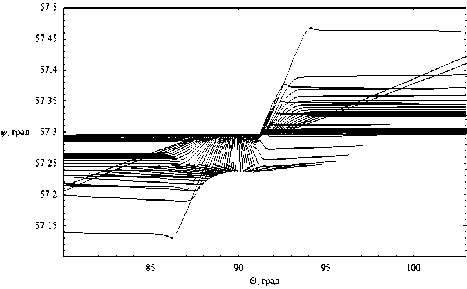
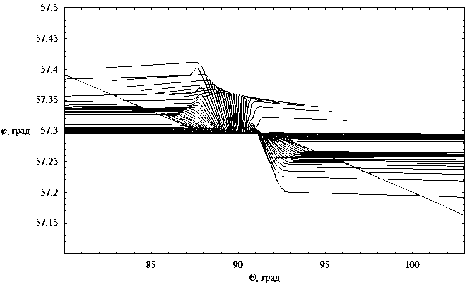
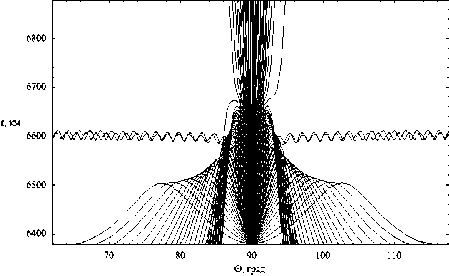
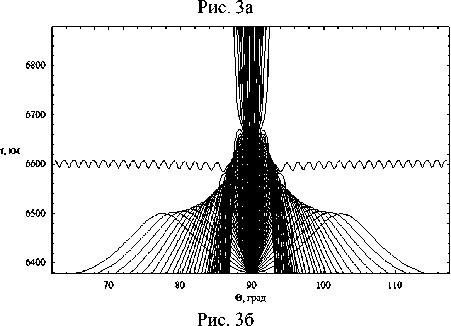
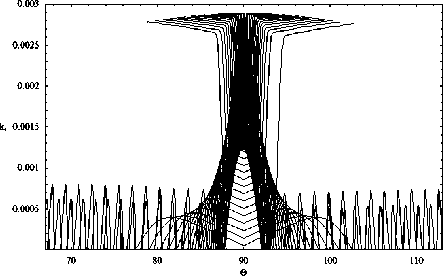
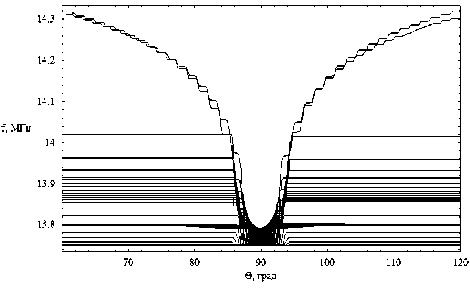
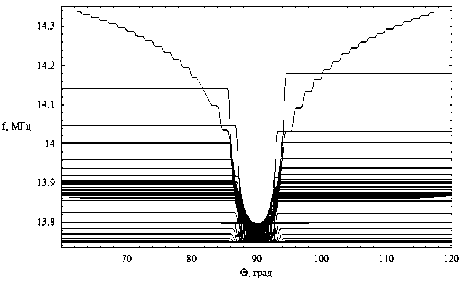
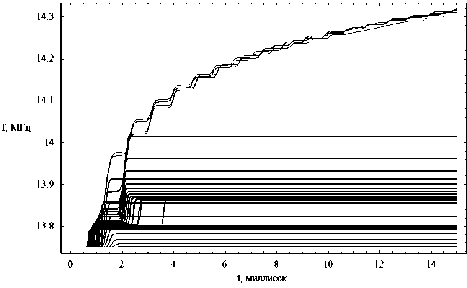
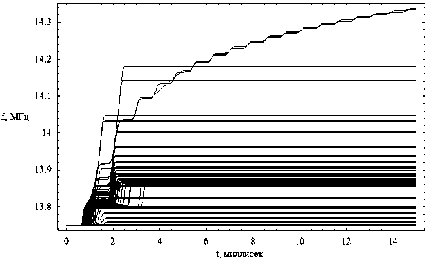
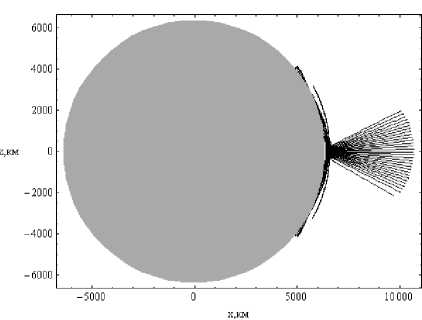
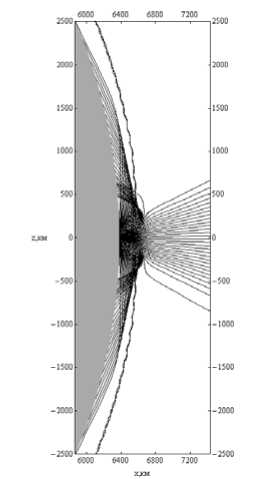
dr = дГ dp = -дГ dm = дГ dt =-дГ dr d к , dr 9 r , dr 9 t ’ dr 9 m ’ где p = (p1, p2, p3) - обобщенный волновой вектор, t[ = (q1, q2, q3) - обобщенные координаты, h1, h2, h3 – коэффициенты Ламе. Поделив уравнения системы (9) на последнее уравнение, получим бихарактеристическую систему d dm _ дГ / d t _ D dt ~ дГ / d m ” ’ параметром вдоль траектории, у которой является групповое время t. Если от обобщенного волнового вектора p перейти к волновому вектору k в криволинейной системе координат [12] p kj= Т-(11) hj и подставить (11) в (10), то получим: dq л dkj 1 Lд = A, j = Bj к, > Aij dt dt hA и ji j = 1, 2, 3; dm = D.(12) dt ВЕСТНИК 2016 В сферической системе координат (2) q1 = r, q2 = θ, q3 = φ, k1 = kr, k2 = kθ, k3 = kφ, а коэффициенты Ламе имеют вид: h1 = hr = 1, h2 = hθ = r, h3 = hφ = r sinθ. (13) Учитывая (13), дифференциальные уравнения для определения компонент волнового вектора несколько упрощаются: dk; = B1, d9 =1 (B2 - k9Aj, dt dt r —- = —(S3 - k (Ax sin9 + A2r cos#)). (14) dt r sinθ3ϕ 1 2 Для определения лучевых траекторий в сферической системе координат необходимо дополнить бихарактеристическую систему (12) начальными условиями: ВЕСТНИК 2016 r(0)=Rz, θ(0)=π2-θs0, ϕ(0)=ϕ0, ω(0) = f0/(2π), kr (0) = ω ε0 cosζcosη, c kθ(0) = ω ε0 sinζcosη, c ω kϕ(0) = c ε0 sinη. (15) В расчетах предполагалось, что η = 0, ε0 = 1, φ0 = 1 рад = 57,3 град, θs0= 0, f0= 13,75 МГц, угол ζ меняется в диапазоне от -89 до 89 градусов. Для вычисления угла α по формуле (6) необходимо знать компоненты вектора k в декартовой системе координат. Их можно найти по формулам: kx=krsinθcosϕ+kθcosθcosϕ-kϕsinϕ, ky=krsinθsinϕ+kθcosθsinϕ-kϕcosϕ, kz = krcosθ- kθsinθ. (16) Рассмотрим результаты численного моделирования. На рис. 1а и 1б представлено лучевое распространение в плоскости (r, φ), то есть в плоскости, перпендикулярной первоначальному направлению распространения радиоволны. Рис. 1а иллюстрирует лучевое распространение обыкновенной волны, рис. 1б – необыкновенной. 57 57 1 57 2 573 574 57 5 57 6 Рис. 1а 57 57 1 57 2 57,3 57 4 57,5 576 Рис. 1б Лучевая структура в плоскости (r, φ); рис. 1а – обыкновенная волна; рис. 1б – необыкновенная волна Хорошо видно, что часть лучевых траекторий проходит ионосферный слой, а другая часть отражается и возвращается на Землю. Некоторая часть лучевых траекторий распространяется в волноводе, возникающем между спорадическим и основным ионосферными слоями. Сравнивая рис. 1а и рис. 1б, находим, что рис. 1б является как бы зеркальным отображением рис. 1а относительно вертикальной оси, но более компактным. Кроме того, интенсивность излучения в межслоевом волноводе в случае обыкновенной волны значительно выше. На рис. 2а и 2б показано распространение в плоскости (θ, φ), то есть в координатах «широта – долгота». (Относительно широты угол θ сдвинут на 90 градусов.) Рис. 2а Рис. 2б Лучевая структура в плоскости (θ, φ); рис. 2а – обыкновенная волна; рис. 2б – необыкновенная волна Это как бы взгляд на лучевые траектории сверху. Как и в предыдущем случае, рис. 2а описывает распространение обыкновенной волны, рис. 2б – необыкновенной. Под действием магнитного поля Земли (внешнего по отношению к источнику излучения) лучевые траектории покидают плоскость первоначального распространения. Если они проходят ионосферу насквозь, то их суммарное отклонение стабилизируется. Если лучи отражаются от ионосферы, то после отражения они стремятся вернуться в плоскость первоначального распространения. Особняком стоят лучи, распространяющиеся в волновом канале. На рис. 2а и 2б – это косые линии. Боковое отклонение таких лучей непрерывно увеличивается при прохождении волнового канала. Сопоставляя рис. 2а и 2б, видим, что рис. 2б является как бы компактным отражением рис. 2а относительно горизонтальной оси. На рис. 3а и 3б представлены проекции лучевых траекторий в плоскости (r, θ), то есть в пло- скости первоначального распространения. Лучевая структура в плоскости (r, θ); рис. 3а – обыкновенная волна; рис. 3б – необыкновенная волна Рис. 3а описывает распространение обыкновенной волны, а рис. 3б – необыкновенной. В этой плоскости лучи образуют по два каустических острия (слева справа относительно источника излучения). Одно выше, а другое ниже волнового канала. Видно, что область многолучевости на поверхности Земли имеет ограниченный размер, область радиосвязи, образовавшаяся благодаря отражению от ионосферы, охватывает зона по 30 градусов. Хорошо видно распространение волны в ионосферном канале. На рис. 4а и 4б показаны проекции бихарактеристик в плоскости (kr, θ). Рис. 4а соответствует обыкновенной волне, а рис. 4б – необыкновенной. Рис. 4а Рис. 4б Лучевая структура в плоскости (kr, θ); рис. 4а – обыкновенная волна; рис. 4б – необыкновенная волна На рисунках можно выделить три группы кривых: 1) линии, поднимающиеся вверх с небольшим отклонением от вертикали, имеющие излом и образующие «шапочку» рисунка, соответствуют лучам, проходящим ионосферный слой; 2) линии, образующие пирамиду, соответствуют отраженным от ионосферы лучам; 3) осциллирующие кривые соответствуют волнам, распространяющимся в волноводе. Как обычно, рисунок, соответствующий обыкновенной волне, выглядит компактнее. ВЕСТНИК 2016 Рис. 5а Рис. 5б Зависимость частоты сигнала fω от угла θ; рис. 5а – обыкновенная волна; рис. 5б – необыкновенная волна ВЕСТНИК 2016 На рис. 5а и 5б показана зависимость частоты сигнала вдоль лучей от угла θ. Рис. 5а соответствует обыкновенной волне, а рис. 5б соответствует необыкновенной волне. Для проходящих лучей изменение частоты распространения происходит на очень небольшом участке, соответствующем спорадическому слою, который образуется, в силу модели, очень быстро. На рисунках – это горизонтальные линии, отделяющиеся от общей образующей. Отраженные лучи заполняют нижнюю часть рисунков, а левую и правую ветви формируют лучи, распространяющиеся в волноводе. На рис. 6а и 6б приведена зависимость частоты сигнала fω от группового времени t. Рис. 6а соответствует обыкновенной волне, а рис. 6б – необыкновенной. В значительной степени рис. 6 повторяют правые половины рис. 5. Отметим, что наибольшие временные задержки при одной и той же дальности распространения характерны для сигналов, распространяющихся в ионосферном волноводе. Рис. 6а Рис. 6б Зависимость частоты сигнала fω от группового времени t; рис. 6а – обыкновенная волна; рис. 6б – необыкновенная волна В заключение приведем рис. 7 и 8, на которых изображены лучевые траектории в декартовой системе координат в соответствии с формулами 2. Рис. 7 Лучевая структура в плоскости (x, z); обыкновенная волна; серый цвет – поверхность Земли Рис. 8 Лучевая структура в плоскости (x, z); фрагмент рис. 7; серый цвет – поверхность Земли Рис. 7 иллюстрирует общее положение источника излучения на поверхности Земли (экваторе), а рис. 8 показывает ход лучевых траекторий в плоскости (x, z) более детально. Таким образом, в работе рассмотрены особенности распространения электромагнитного излучения в неоднородной, анизотропной, нестационарной ионосферной плазме при условии образования спорадического волнового возмущения. Расчеты проведены как в случае обыкновенной волны, так и для необыкновенной волны. При изучении лучевой структуры нами применялась бихарактеристическая система дифференциальных уравнений в сферических координатах, неизвестным в которой являлись сферические координаты луча, компоненты волнового вектора, а также частота (меняющаяся в условиях нестационарности среды распространения) и групповое время.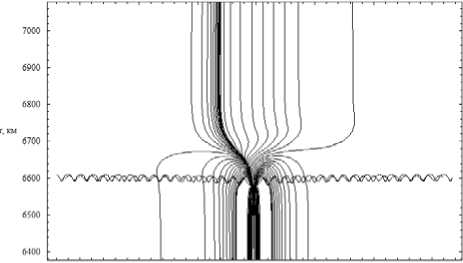
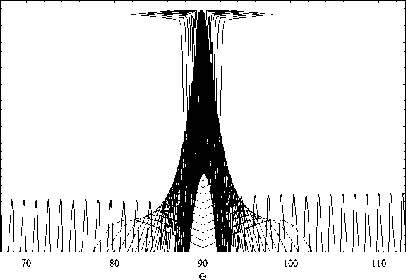
Список литературы Математическое моделирование распространения радиоволн в нестационарной плазме с учетом кривизны поверхности Земли и ионосферных слоев
- Крюковский А.С., Лукин Д.С., Растягаев Д.В. Математическое моделирование распространения радиоволн в анизотропной неоднородной ионосфере//Вестник Российского нового университета. -2009. -Выпуск 2. Управление, вычислительная техника и информатика. -С. 7-14.
- Крюковский А.С., Растягаев Д.В., Скворцова Ю.И. Исследование распространения частотно-модулированных пространственно-временных сигналов в неоднородной анизотропной ионосфере//Вестник Российского нового университета. -2013. -Выпуск 4. Управление, вычислительная техника и информатика. -С. 47-52.
- Крюковский А.С., Растягаев Д.В., Скворцова Ю.И. Распространение частотно-модулированных пространственно-временных радиоволн в анизотропной ионосфере//Труды XXIV Всероссийской научной конференции «Распространение радиоволн» (29 июня -5 июля 2014, Иркутск). -Иркутск: ИСЗФ СО РАН, 2014. -Т. 4. -С. 126-129.
- Крюковский А.С., Скворцова Ю.И. О распространении частотно-модулированного излучения в ионосферной плазме//Цивилизация знаний: российские реалии: труды XV Международной научной конференции (Москва, 25-26 апреля 2014 г.) -М.: РосНОУ, 2014. -Часть 2. -С. 436-438.
- Крюковский А.С., Лукин Д.С., Растягаев Д.В., Скворцова Ю.И. Моделирование распространения частотно-модулированного радиоизлучения в ионосферной плазме//V Всероссийские Армандовские чтения : Сверхширокополосные сигналы в радиолокации, связи и акустике: материалы V Всероссийской научной конференции (Муром, 26.06.-1.07.2015 г.). -Муром: Изд.-полиграфический центр МИ ВлГУ, 2015. -237 с. -С. 131-137.
- Крюковский А.С., Лукин Д.С., Растягаев Д.В., Скворцова Ю.И. Математическое моделирование распространения частотно-модулированных радиоволн в ионосферной плазме//Радиотехника и электроника. -2015. -Т. 60. -№ 10.
- Крюковский А.С., Лукин Д.С., Кирьянова К.С. Метод расширенной бихарактеристической системы при моделировании распространения радиоволн в ионосферной плазме//Радиотехника и электроника. -2012. -Т. 57. -№ 9. -С. 1028-1034.
- Кирьянова К.С., Крюковский А.С. Особенности лучевого распространения радиоволн в ионосфере Земли//T-Comm: Телекоммуникации и транспорт. -2012. -№ 11. -С. 25-28.
- Кирьянова К.С., Крюковский А.С. Особенности лучевых траекторий в окрестности ионосферной локальной неоднородности с пониженной электронной концентрацией//Электромагнитные волны и электронные системы. -Радиотехника, 2012. -Т. 17. -№ 9. -С. 42-47.
- Кирьянова К.С., Крюковский А.С. Влияние локальных ионосферных неоднородностей на распространение декаметровых радиоволн//Физические основы приборостроения. -М.: НТЦ УП РАН, 2012. -Т. 1. -№ 3. -С. 19-25.
- Kiryanova, K.S., Kryukovsky, A.S., Lukin, D.S. Simulation of decametric wave propagation in the ionospheric plasma//Revista de Matematica. Teoria y Aplicaciones. -2013. -V. 20. -№ 1. -P. 21-34.
- Кравцов Ю.А., Орлов Ю.И. Геометрическая оптика неоднородных сред. -М.: Наука, 1980. -304 с.
- Крюковский А.С. Равномерная асимптотическая теория краевых и угловых волновых катастроф: монография. -М.: РосНОУ, 2013. -368 с.
- Крюковский А.С. Необходимые и достаточные условия образования основных волновых катастроф с корангом, равным двум//Распространение и дифракция электромагнитных волн: междувед. сб. -М.: МФТИ, 1993. -С. 4-19.
- Крюковский А.С., Лукин Д.С. Локальная асимптотика быстроосциллирующих интегралов, описывающих волновое поле в областях фокусировки//Дифракция и распространение электромагнитных волн: междувед. сб. -М.: МФТИ, 1984. -С. 39-53.
- Крюковский А.С., Скворцова Ю.И. Применение теории катастроф для описания пространственно-временной структуры частотно-модулированного сигнала в плазме//Электромагнитные волны и электронные системы. -2013. -Т. 18. -№ 8. -С. 18-23.
- Дорохина Т.В., Крюковский А.С., Растягаев Д.В. Принципы разработки мультимедийной информационной системы «Волновые катастрофы в радиофизике, акустике и квантовой механике»//Россия: перспективы прорыва в цивилизацию знаний. Информационные системы и компьютерные технологии: тезисы докл. V Межвузовской научной конференции Российского нового университета, 16-17.04.2004 г. -М.: РосНОУ, 2004. -С. 291-293.
- Дорохина Т.В., Ипатов Е.Б., Крюковский А.С., Лукин Д.С., Палкин Е.А., Растягаев Д.В. Математическое компьютерное моделирование волновых полей типа катастроф//Распространение радиоволн: сборник докладов XXI Всероссийской научной конференции, Йошкар-Ола, 25-27 мая 2005 г. -Йошкар-Ола: МарГТУ, 2005. -Т. 2. -С. 336-339.
- Дорохина Т.В., Крюковский А.С., Лукин Д.С., Волкова Е.В., Костьо А.О., Павлова М.В. Создание информационной системы волновой теории катастроф и её применение при математическом моделировании//Вестник Российского нового университета. -2007. -Выпуск 2. Управление, вычислительная техника и информатика. -С. 91-107.


