Математическое моделирование развития трещин в толще пород над отработанными пластами калийных солей

Особенности проявления горного давления вокруг очистных выработок обусловлены их большими размерами по сравнению с мощностью отрабатываемых пластов. Размеры выработок, сопоставимых с глубиной отработки, соответствуют значительные объемы породных массивов, затронутых их влиянием. Развитие зон дефектов в подработанных слоях пород может привести к обрушениям в выработанное пространство и образованию трещин на значительную высоту.

Для соляных месторождений существенна проблема предотвращения проникновения пресных вод по трещинам в выработанное пространство, в результате чего может погибнуть рудник, а для угольных месторождений и рудников с нерастворимыми породами – проблема чрезмерного притока воды. Обе проблемы связаны с прогнозом образования зон водопроводящих трещин, возникающих в деформирующихся массивах горных пород в результате выемки рудных залежей.

В мировой практике насчитывается более 80 калийных рудников и соляных шахт, затопленных в результате поступления надсолевых вод в выработанное пространство [1]. На Верхнекамском месторождении произошло два аварийных затопления рудников по трещинам, возникшим в толще пород над отработанными калийными пластами. Принято считать, что на Верхнекамском месторождении водозащитная толща (ВЗТ) представляет собой безводную и водонепроницаемую часть геологического разреза, расположенную между кровлей верхнего отрабатываемого пласта калийно-магниевых солей и кровлей верхнего пласта каменной соли. По строению и составу пород в водозащитной толще выделяется три части: нижняя (ВЗТ1) – чередование пластов калийно-магниевых солей и каменной соли, средняя (ВЗТ2) – покровная каменная соль и верхняя (ВЗТ3) – ритмично чередующиеся между собой пласты каменной соли и мергелей.

Сложность описания и моделирования толщи связана с неоднородностью и частичной нарушенностью породных глинистомергелистых и соляных слоев. Так, каменная соль имеет субгоризонтальную слоистость, содержит глинистые включения и прослойки Прослои тонкослоистой глины разорваны многочисленными субвертикальными трещинами шириной 0,1-3,0 см, выполненными каменной солью. Такое или похожее описание можно отнести к большинству слоев каменной соли.

Слои ритмопачек ВЗТ 3 также имеют сложное строение, например мергель серый прослоями (0,1-5,0 см), темно-серый с прослойками (до 2 мм) ангидрита светло-серого. Порода плотная, средней крепости, местами разорванная тонкими субвертикальными трещинами шириной до 1 мм, выполненными серой каменной солью. В верхней части интервала -прослои (2,0-9,0 см) светло-серой мелкозернистой каменной соли. Слоистость под углом 0º-20º.

Аналогично выглядит описание карналлитовых слоев ВЗТ1: карналлитовая порода оранжевая, красновато-оранжевая, средне- и крупнозернистая с включениями и прослоями (1,0-4,0 см) каменной соли желтовато-серой, серой, мелко- и среднезернистой, с глинистыми включениями и прослойками (1-2 мм). Слоистость под углом 0-10º.

Таким образом, все слои пород, составляющие ВЗТ, подвержены влиянию естественных факторов, которые ослабляют их прочностные и деформационные свойства по ориентированным площадкам, и которыми нельзя пренебрегать при оценке развития деформаций и разрушений.

Оценка развития водопроводящих трещин может быть выполнена только методом математического моделирования. Решение задач о нарушении сплошности подработанных толщ при решении задачи в упруго - пластической постановке [2] не позволяет учитывать ослабления и их ориентацию существующую в слоях пород.

С этой целью используется метод моделирования разрушающихся массивов горных пород [3]. В предлагаемой модели моделирование разрушения пород вокруг выработок рассматривается как процесс развития существующих и образования новых систем дефектов [4, 5]. Метод адаптирован к численному методу конечных элементов, который позволяет учитывать неоднородность деформационных и прочностных свойств пород в массиве с достаточной дробностью.

Варианты возможного направления развития процессов ослабления в каждой точке массива, затрагиваемой влиянием техногенного вмешательства или природных сил, заранее не определены. Их бесконечное множество. На феноменологическом уровне (без рассмотрения физических аспектов разрушения) проблема многовариантности разрешается путем рассмотрения ограниченного количества систем плоских дефектов или ослаблений с фиксированными направлениями. Идея метода заключается в том, что в каждой точке массива (в каждом отдельном элементе) в процессе моделирования на всех этапах нагружения рассматривается ограниченное количество направлений, по которым возможны разрушения при сдвиге или разрыве.

Рассматриваются направления площадок ослаблений с шагом 45°. При этом 13 направлений покрывают все возможные случаи (рис. 1).

Такой подход позволяет при численных расчетах перебирать возникающие условия по всем выделенным направлениям на каждом этапе нагружения. При этом автоматически учитываются влияние поворотов главных осей тензора напряжений, когда активное разрушение может происходить то по одним, то по другим различно ориентированным площадкам.

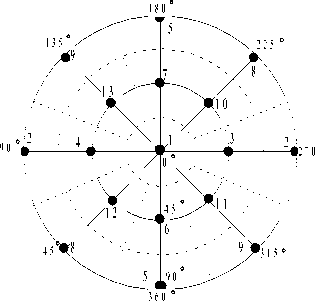
Рис.1. Проекция на плоскость сферической диаграммы фиксированных направлений систем трещин в пространстве. Зоны внутри штриховых контуров определяют множество направлений, относящихся к соответствующей системе трещин.

Точки на диаграмме (рис. 1) определяют плоскости, касательные к сферической поверхности, которые указывают ориентацию поверхностей с дефектами. В общем случае в точке массива каждая система ослаблений может характеризоваться одним или несколькими параметрами, с помощью которых описывают прочность на сдвиг и на растяжение, а также другие свойства элемента массива.

Применяется однопараметрическое задание прочности систем нарушений. Каждая из систем характеризуется величиной p i ( i = 1, 2,  ,

13), определяющей меняющуюся в процессе разрушения прочность. В начальный момент времени ^{p i} могут быть равными единице (при отсутствии ослаблений по соответствующим направлениям) или меньшими единицы, если в соответствующей системе имеются ослабления: трещины, слабые контакты или прослойки пластичных пород. Параметры p i определяет относительную прочность на разрыв при растяжении поперек плоскости трещин, относительную прочность на сдвиг в условиях сжатия и сцепление по плоскостям нарушений (имеется в виду прочность относительно ненарушенного состояния).

Дефекты,    образующие    ориентированные    системы,    не рассматриваются как отдельные объекты, но их состояние, описываемое соответствующими параметрами, учитывается в поведении конгломерата сплошного материала и дефектов. Напряжения и деформации в таком конгломерате считаются непрерывными и рассчитываются как для сплошной среды с учетом анизотропии, вызванной ориентированными ослаблениями.

Под действием напряжений элемент массива разрушается (теряет часть начальной прочности) по некоторым поверхностям в результате сдвига при сжатии, раскалывания либо разрыва. Какой из возможных вариантов разрушения реализуется в данный момент, определяется действующими напряжениями, направлением главных осей тензора напряжений и состоянием дефектов по разным направлениям.

Приращение полной деформации элемента среды d    d e d ve d p d

где d ^е – приращение линейно–упругих обратимых деформаций;

d ^ve – приращение обратимых вязкоупругих деформаций;

d ^р – приращение пластических деформаций;

d ^r – приращение разрушающих деформаций;.

В каждой точке среды для каждого из выделенных направлений применяется критерий прочности Кулона – Мора, дополненный условием прочности на разрыв и раскалывание в следующей форме:

n = KP i+°n шф при ° n > °;

°n= F i(^Gp P i , ^ac , °, ) при ° n <0; G t =F2^ c , G n ) при G n <°,

где σ n , σ t и τ n – нормальные и касательные напряжения в плоскости нарушения с номером i ;

K и φ – соответственно сцепление и угол трения в ненарушенном материале;

pi и p’i   – параметры, характеризующие снижение прочности соответственно на сдвиг и разрыв, по i–й поверхности ослабления);

F 1 .– определяет сопротивление разрыву в зависимости от условий объемного напряженного состояния.

В общем случае разрушение материала по любому направлению сопровождается одновременным снижением величины сцепления и прочности на разрыв.

Упругие деформации пород также рассчитываются с учетом анизотропии, существовавшей в естественных условиях и приобретенной в результате развития ориентированных дефектов.

Для оценки условия состояния на поверхности возможного разрушения используется понятие степени нагруженности, которое определяется в зависимости от действующих напряжений в плоскости и по нормали к ней. Так для проверки возможного сдвига на площадке n вычисляется степень нагруженности по сдвигу на i -й площадке, определяющая возможность пластического сдвига или разрушения,

KPi + m_n tg9

При c ≥ 1 происходит мгновенное снижение прочности, при c ≥ c дл прирастает ослабление за действующий промежуток времени ( c дл < 1 – коэффициент длительной прочности). Аналогично рассчитывается условие возможного разрушения при разрыве, когда величина напряжения сравнивается с прочностью при растяжении.

n c

^Fp &p P i^,Cс , ^t ) .

Связь между приращениями деформаций и прочности в элементарном объеме представлена в виде dp  M„ p*; или dp=-Mc p|d,n |

где dp – приращение относительной прочности по системе трещин или по определенному направлению;

ⁿ – приращения растягивающих деформаций в направлении нормали к плоскости нарушения (при разрыве);

^{d nr} – приращения сдвиговых разрушающих деформаций в плоскости дефектов;

M p и М с – коэффициенты, играющие роль локальных модулей спада при разрыве и сдвиге;

Коэффициенты M p и М с являются безразмерными величинами. Они определяют модули спада, отнесенные к величине текущей прочности. Коэффициенты спада зависят от вида разрушения.

С использованием описанного метода, выполнено математическое моделирование деформирования массива и развития в нем водопроводящих трещин при отработке двух сближенных сильвинитовых пластов на одном из участков Верхнекамского месторождения. Решение выполняется в постановке плоской деформации. При этом нумерация систем ослаблений выполняется с учетом симметрии процессов относительно плоскости деформации (рис. 2).

Рис. 2. Схема 12 систем трещин, учитываемых в условиях плоской деформации. Системы 5, 6, 7 и 8 – парные.

Исследуется ситуация последовательной отработки на протяженном участке шириной 400 м сначала верхнего, затем нижнего пласта. Зона отработанного пространства с оставленными целиками представляется материалом с эквивалентными упругими свойствами.

Параметром, определяющим влияние на деформирование толщи, служит величина максимального оседания кровли верхнего отрабатываемого пласта через длительное время после отработки. Величина максимального оседания кровли пласта зависит от извлечения, заполнения камер закладочным материалом и его усадкой. Максимальное оседание кровли верхнего пласта при отработке двух сближенных пластов определяется суммой максимальных оседаний кровли каждого из пластов.

Физико-механические свойства пород, принятые в расчетах, относятся к участку с пониженными прочностными свойствами соляных пород на Верхнекамском месторождении (табл. 1).

Таблица 1.

Физико-механические свойства горных пород.

Порода	Модуль упругости, МПа	Коэф. Пуассона	σ с , МПа	σ r , МПа	ф,	K L	K pl	M .	K ve	K V
Сильвинит	3500	0,25	15,0	1,70	350	0,5	2,5	80	6,0	0,7
Карналлит	1500	0,25	7,0	0,9	40	0,5	1,4	100	2,0	0,7
Каменная соль	8300	0,19	15,0	1,2	37	0,5	3,0	50	4,0	0,7
СМТ	3000	0,22	10,0	1,2	35	0,7	0,3	60	2,0	0,7
ТКТ	5500	0,23	20,0	0,7	30	0,7	0,3	200	1,0	0,7
Аргилит-песчаник-алевролит	1000	0,2	8,0	0,8	25	0,5	0,2	200	3,0	0,6
Песчаник	5000	0,2	40	4	30	0,7	1,0	200	0,4	0,6
Алевролит разрушенный	1000	0,3	12	1,2	30	0,8	0,8	100	0,3	0,3
Глина, четвертичные отложения	500	0,3	10	1,0	20	0,6	1,5	30	0,3	0,6

Примечание:

σ с , – прочность при сжатии;

σ r – прочность при растяжении;

ф – угол внутреннего трения;

K L , – относительная длительная прочность;

K pl – коэффициент пластичности;

M – модуль локального спада;

K ve – коэффициент относительной вязкости;

K V – коэффициент объемного расширения при сдвиговом разрушении.

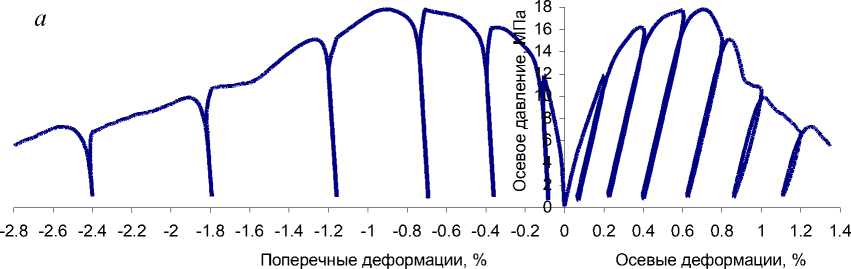
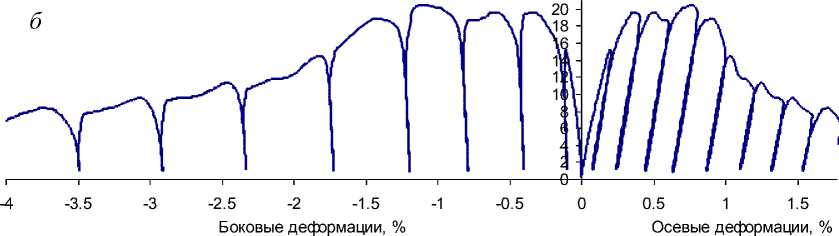
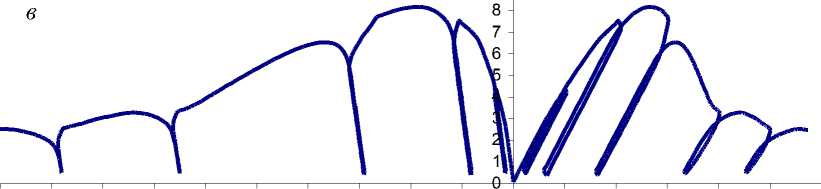
Расчетные диаграммы одноосного нагружения образцов сильвинита, каменной соли и карналлита с принятыми параметрами свойств приведены на рис. 3.

-1    -0.9   -0.8   -0.7   -0.6   -0.5   -0.4   -0.3   -0.2   -0.1     0     0.1    0.2    0.3    0.4    0.5    0.6

Боковые деформации,%                 Осевые деформации, %

Рис. 3. Расчетные диаграммы одноосного нагружения образцов сильвинита (а), каменной соли (б) и карналлита (в).

При моделировании учитывалось, что слои пород имеют ориентированные дефекты (табл. 2).

Расчеты выполнены с помощью программного комплекса DESTROCK PLANE [8]. Начальные напряжения в массиве рассчитывались с учетом вязких свойств пород [6, 7]

Моделирование выполнено для случаев максимального оседания кровли верхнего отработанного пласта 3 м, 2,5 м, 2,3 м и 2 м. (рис. 4). Поскольку задача заключается в том, чтобы оценить последствия после длительного времени после отработки, то расчеты для каждого случая выполняются независимо. Для этого свойства эквивалентной среды отработанных участков слоев в каждом варианте задаются разными, позволяющими достичь необходимой величины конвергенции почвы и кровли в средней части участка.

Таблица 2

Характеристики ослаблений по поверхностям в слоях пород

Порода	Коэффициент ослабления по площадкам
	1	2	3	4	5-8
Сильвинит	0,6	1,0	0,8	0,8	1,0
Карналлит	0,8	1,0	0,9	0,9	1,0
Каменная соль	0,6	0,6	0,8	0,8	1,0
СМТ	0,7	0,7	0,8	0,8	0,9
ТКТ	0,3	0,3	0,5	0,5	0,7
Аргилит-песчаник-алевролит	0,5	0,5	0,5	0,5	0,5
Песчаник	0,6	0,6	0,7	0,7	0,8
Алевролит разрушенный	0,5	0,5	0,5	0,5	0,5
Глина, четвертичные отложения	0,9	0,9	0,9	0,9	0,9

Примечание: 1. Нумерация площадок приведена на рис.2.

а

‘ в н и g Л ir j

и	Глина, четвертичные отложения
	Алевролит
	Песчаник                                  __
50		Аргиллит		I1 '.      1
		Песчаник		= 'l I1 J \
		Алевролит		h I1 _lL2i______
100 150		Терригено- карбонатная		= =i=l
200	н о о о о Е ГС	толща		г = =i
	I т сС	Соля но-
250	о О	мергелистая толща		ч = i= = i== L=____
300		Покровная каменная соль		L-==
	—			—   —---- Х--“     . L
350	=	_плас юв = калийно- = магниевых
	—
	—	= каменной	—  - — . —=
		— соли	2

б

100	= =     1
	= =    У
	- = 1 =
	==|=|
150	Терригено- = =   ।
	карбонатная      = =
	1 толща 1
200	1 1 1 1 1                                                    ________________________________________________________________
	1 1 Соляно-              1।
250	мергелистая          1
	толща              । I1
	Покровная           z=
300	_ —--
	каменная              __
	= =  —
	соль                   ===-=

в

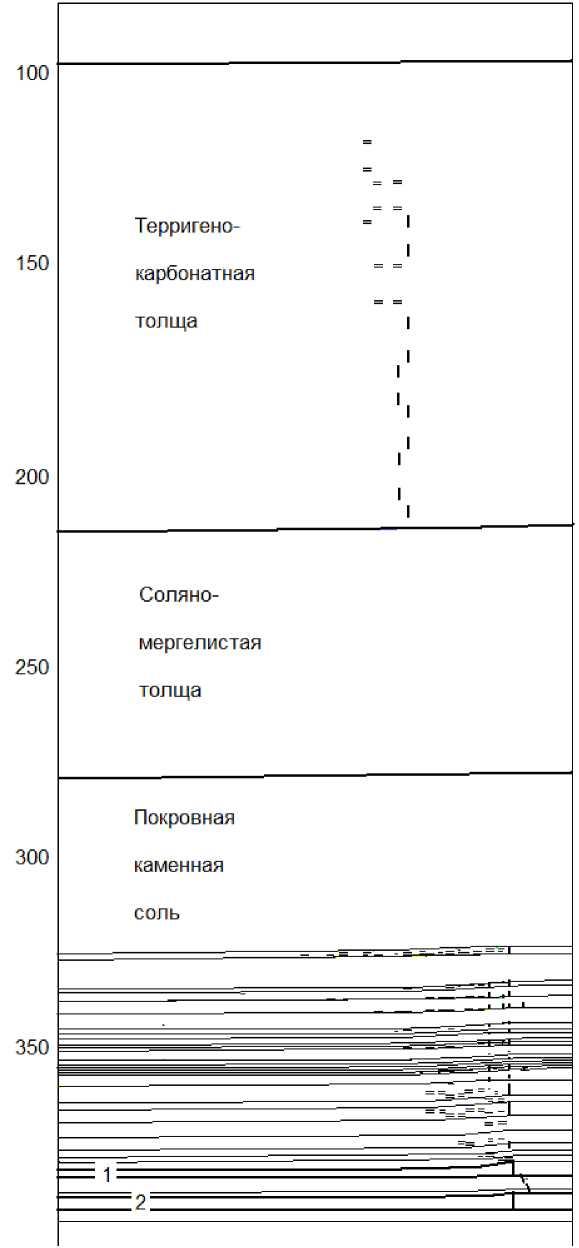
Рис.4. Расчетная картина распределения трещин после отработки сближенных сильвинитовых верхнего (1) и нижнего (2) пластов при максимальном оседании кровли верхнего пласта на 3 м, 2,5 м, 2,3 м и 2 м ( а,б,в,г ).

Штрихи указывают расположение и ориентацию возникших трещин; к.с. - слой каменной соли в карналитовой зоне.

С течением времени с ростом максимального оседания кровли верхнего пласта в породах возникают и развиваются ориентированные плоские дефекты. До некоторого момента эти ослабления не нарушают водозащитных свойств. Здесь принято считать, что ослабления становятся водопроводящими, если степень ослабления становится меньше 0,15.

В результате моделирования получены следующие результаты. При максимальном оседании кровли верхнего пласта 3,0 м водопроводящие трещины пересекают все слои ВЗТь покровную каменную соль (ВЗТ2), ритмично чередующиеся между собой пласты каменной соли и мергелей (ВЗТ3). Трещины распространяются выше в терригено-карбонатную толщу

(ТКТ) и толщу перемежающихся слоев аргиллита, песчаника и алевролита (рис. 4, а).

При максимальном оседании кровли верхнего пласта 2,5 м трещины также пересекают ВЗТ 1 , ВЗТ 2 и ВЗТ 3 , они распространяются до кровли терригено-карбонатной толши (рис. 4, б). Так же, как и в первом случае, водозащитные свойства толщи пород будут нарушены.

При максимальном оседании кровли верхнего пласта 2,3 м трещины распространяются в ВЗТ1 , однако в некоторых слоях каменной соли они не возникают. В ВЗТ2 и ВЗТ3 трещины не образуются, однако они появляются в ТКТ (рис. 4, в). В этом случае водозащитные свойства толщи налегающих пород не нарушают водозащиту отработанного участка, Мощные пачки покровной каменной соли и соляно-мергельной толщи обеспечат водозащиту отработанному участку.

При максимальном оседании кровли верхнего пласта 2 м трещины не выходят за пределы ВЗТ 1 . Трещины пересекают все слои каменной соли, в том числе маломощные, кроме самого верхнего (рис. 4, г).

Приведенные примеры расчетов показали, что метод деформирования разрушающихся горных пород, реализуемый с помощью программного комплекса DESTROCK PLANE, позволяет моделировать геомеханические процессы в толще вмещающих пород при разработке пластовых месторождений калийных солей.

Параметры состояния, которые закладываются в исходные данные для расчетов методами механики сплошной среды, учитывают не только деформационные и прочностные свойства в ненарушенном состоянии, но характеристики существующих систем ослаблений. Метод не нуждается в других оценочных критериях условий разрушения, с использованием таких понятий как зоны расслоения, растягивающие деформации, искривление балок или чего-либо подобного. Задача заключается в том, чтобы с максимальной полнотой учесть физико-механические свойства и начальные ослабления прочности, существующие в слоях пород водозащитной толщи.